Tìm số giao điểm của đồ thị hàm số $y = {x^3} - 3{x^2} + 2$ và $y = - {x^2} + 7x - 11$
-
A.
$0$
-
B.
$2$
-
C.
$1$
-
D.
$3$
Số giao điểm của đồ thị hàm số $y = f\left( x \right)$ và đồ thị hàm số $y = g\left( x \right)$ bằng số nghiệm của phương trình $f\left( x \right) = g\left( x \right)$
Xét phương trình
$\begin{array}{l}{x^3} - 3{x^2} + 2 = - {x^2} + 7x - 11\\ \Leftrightarrow {x^3} - 3{x^2} + 2 - \left( { - {x^2} + 7x - 11} \right) = 0\\ \Leftrightarrow {x^3} - 2{x^2} - 7x + 13 = 0\end{array}$
Xét hàm số \(y = f\left( x \right) = {x^3} - 2{x^2} - 7x + 13\) trên tập số thực \(\mathbb{R}\) có:
\(f'\left( x \right) = 3{x^2} - 4x - 7 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \dfrac{7}{3}\end{array} \right.\)
Bảng biến thiên
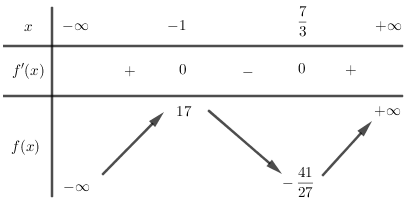
Quan sát bảng biến thiên ta thấy hàm số có \({y_{CD}}.{y_{CT}} < 0\) nên phương trình \(y = 0\) có \(3\) nghiệm phân biệt.
Đáp án : D

Các bài tập cùng chuyên đề
Bài 1 :
Cho hàm số $y = {x^4} - 2m{x^2} + {m^2} + m.$ Tất cả các giá trị của $m$ để đồ thị hàm số có $3$ điểm cực trị tạo thành tam giác có một góc ${120^o}$ là:
-
A.
$m = \dfrac{1}{{\sqrt[3]{3}}}$
-
B.
$m = 0;\,m = \dfrac{1}{{\sqrt[3]{3}}}$
-
C.
$m = \dfrac{1}{{\sqrt[3]{2}}}$
-
D.
$m = 1$
Bài 2 :
Số giao điểm của hai đồ thị hàm số $y = 3{x^2}$ và $y = {x^3} + {x^2} + x + 1$ là:
-
A.
$0$
-
B.
$1$
-
C.
$2$
-
D.
$3$
Bài 3 :
Cho hàm số \(y = 3{x^4} + 2\left( {m - 2018} \right){x^2} + 2017\) với \(m\) là tham số thực. Tìm giá trị của \(m\) để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có một góc bằng \({120^0}\).
-
A.
\(m = - 2018.\)
-
B.
\(m = - 2017.\)
-
C.
\(m = 2017.\)
-
D.
\(m = 2018.\)
Bài 4 :
Đồ thị của đạo hàm bậc nhất \(y = f'\left( x \right)\) của hàm số f(x) được cho trong Hình 1.13:
a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.
b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.

Bài 5 :
Đường cong trong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
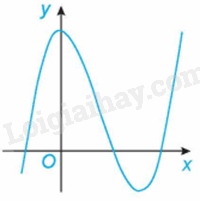
A. \(y = - {x^3} + 3{x^2} + 1\).
B. \(y = {x^3} - 3{x^2} + 3\).
C. \(y = - {x^2} + 2x + 1\).
D. \(y = \frac{{x + 1}}{{x - 1}}\).
Bài 6 :
Cho hai hàm số \(y = f\left( x \right),y = g\left( x \right)\) có đồ thị hàm số lần lượt ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.
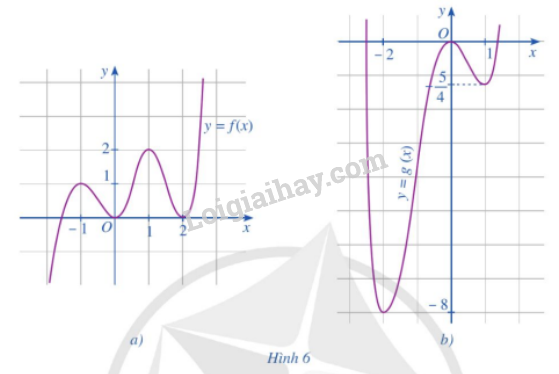
Bài 7 :
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.

Bài 8 :
Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau:
a) \(y = 4{x^3} + 3{x^2}--36x + 6\)
b) \(y = \frac{{{x^2} - 2x - 7}}{{x - 4}}\)
Bài 9 :
Đạo hàm f'(x) của hàm số y = f(x) có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số y = f(x).
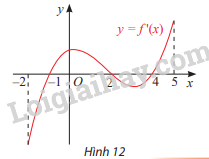
Bài 10 :
Cho hàm số f(x) xác định trên R có bảng biến thiên như sau:

a) Hàm số f(x) đồng biến trên mỗi khoảng (0;2) và (2;3)
b) Số điểm cực trị của hàm số đã cho là 5
c) Hàm số f(x) có giá trị lớn nhất bằng 3
d) Đồ thị hàm số không có đường tiệm cận
Bài 11 :
Ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc \({120^o}\) và có độ lớn lần lượt là 25 N và 12 N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn 4 N. Tính độ lớn (đơn vị: N) của hợp lực của ba lực trên (làm tròn kết quả đến hàng đơn vị).
Bài 12 :
Giá trị của tham số m để đồ thị hàm số \(y = {x^3} - 3{x^2} + m\) có hai điểm cực trị A, B thỏa mãn OA = OB (O là gốc tọa độ) có dạng \(\frac{a}{b}\) là một phân số tối giản. Tính a + b.
Bài 13 :
Hình bên là đồ thị của hàm số f’(x). Hỏi hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
-
A.
\((2; + \infty )\)
-
B.
\((1;2)\)
-
C.
\((0;1)\)
-
D.
\((0;1)\) và \((2; + \infty )\)
Bài 14 :
Giả sử một công ty du lịch bán tour với giá là x /khách thì doanh thu sẽ được biểu diễn qua hàm số \(f(x) = - 200{x^2} + 550x\). Công ty phải bán giá tour cho một khách là bao nhiêu (đơn vị: triệu đồng) để doanh thu từ tua xuyên Việt là lớn nhất (kết quả làm tròn đến hàng phần trăm)?
Bài 15 :
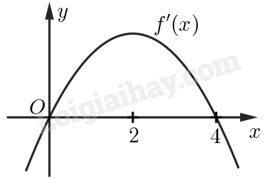
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và đạo hàm \(f'\left( x \right)\) có đồ thị như hình bên. Sử dụng đồ thị của hàm số \(y = f'\left( x \right)\), hãy cho biết:
a) Các khoảng đồng biến, khoảng nghịch biến của hàm số \(f\left( x \right)\);
b) Hàm số \(f\left( x \right)\) có cực đại, cực tiểu không? Nếu có, hãy cho biết các điểm cực trị tương ứng.
Bài 16 :
Tìm các khoảng đồng biến, khoảng nghịch biến và cực trị (nếu có) của các hàm số sau:
a) \(y = {x^3} - 9{x^2} - 48x + 52\);
b) \(y = - {x^3} + 6{x^2} + 9\).
Bài 17 :
Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau:
a) \(y = x + \frac{1}{x}\);
b) \(y = \frac{x}{{{x^2} + 1}}\).
Bài 18 :
Tìm các khoảng đơn điệu và các cực trị (nếu có) của các hàm số sau:
a) \(y = {x^4} - 2{x^2} + 3\);
b) \(y = {x^2}\ln x\).
Bài 19 :
Chứng minh rằng hàm số \(f\left( x \right) = \sqrt[3]{{{x^2}}}\) không có đạo hàm tại \(x = 0\) nhưng có cực tiểu tại điểm \(x = 0\).
Bài 20 :
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = - x\left( {2x - 5} \right),\forall x \in \mathbb{R}\). Khẳng định nào dưới đây đúng?
A. \(f\left( { - 2} \right) < f\left( { - 1} \right)\).
B. \(f\left( 0 \right) > f\left( 2 \right)\).
C. \(f\left( 3 \right) > f\left( 5 \right)\).
D. \(f\left( 3 \right) > f\left( 2 \right)\).
Bài 21 :
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như Hình 7. Số điểm cực trị của hàm số \(y = f\left( x \right)\) là:
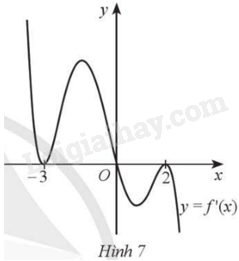
A. 4.
B. 3.
C. 2.
D. 1.
Bài 22 :
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
Cho hàm số \(y = {x^3} - 3{\rm{x}} + 2\).
a) \(y' = 3{{\rm{x}}^2} - 3\).
b) \(y' = 0\) khi \(x = - 1,x = 1\).
c) \(y' > 0\) khi \(x \in \left( { - 1;1} \right)\) và \(y' < 0\) khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\).
d) Giá trị cực đại của hàm số là ${{f}_{C}}=0$.
Bài 23 :
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
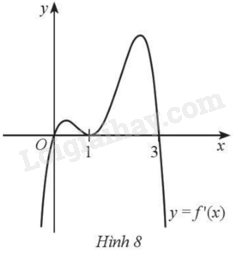
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như Hình 8.
a) \(f'\left( x \right) = 0\) khi \(x = 0,x = 1,x = 3\).
b) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\).
c) \(f'\left( x \right) > 0\) khi \(x \in \left( {0;3} \right)\).
d) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {0;3} \right)\).
Bài 24 :
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
Cho hàm số \(y = {2^{{x^2} - 1}}\).
a) \(y' = \left( {{x^2} - 1} \right){.2^{{x^2} - 2}}\).
b) \(y' = 0\) khi \(x = - 1,x = 1\).
c) \(y\left( { - 2} \right) = 8,y\left( { - 1} \right) = 1,y\left( 1 \right) = 1\).
d) Trên đoạn \(\left[ { - 2;1} \right]\), hàm số đạt giá trị nhỏ nhất bằng 1, giá trị lớn nhất bằng 8.
Bài 25 :
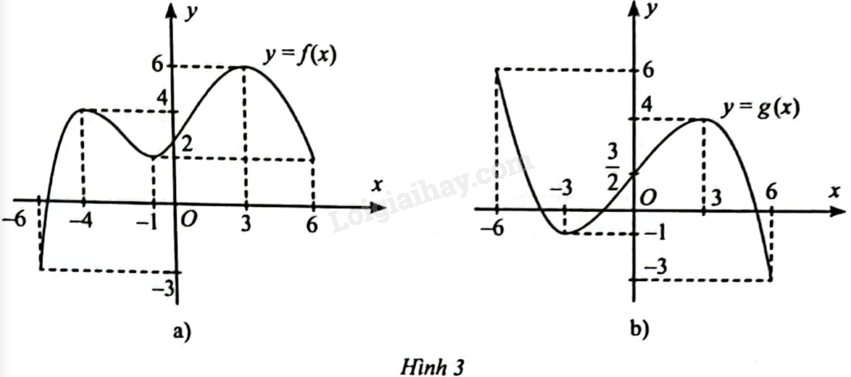
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 3.
Bài 26 :
Xét tính đơn điệu và tìm cực trị của các hàm số:
a) \(y = - {x^3} - 3{x^2} + 24x - 1\);
b) \(y = {x^3} - 8{x^2} + 5x + 2\);
c) \(y = {x^3} + 2{x^2} + 3x + 1\);
d) \(y = - 3{x^3} + 3{x^2} - x + 2\).
Bài 27 :
Xét tính đơn điệu và tìm cực trị của các hàm số:
a) \(y = \frac{{3{\rm{x}} + 1}}{{{\rm{x}} - 2}}\);
b) \(y = \frac{{2{\rm{x}} - 5}}{{3{\rm{x}} + 1}}\);
c) \(y = \sqrt {4 - {x^2}} \);
d) \(y = x - \ln {\rm{x}}\).
Bài 28 :
Xét tính đơn điệu và tìm cực trị của các hàm số:
a) \(y = \frac{{{x^2} + 8}}{{x + 1}}\);
b) \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\);
c) \(y = \frac{{ - 2{x^2} + x + 2}}{{2x - 1}}\);
d) \(y = \frac{{ - {x^2} - 6x - 25}}{{x + 3}}\).
Bài 29 :
Đạo hàm \(f'\left( x \right)\) của hàm số \(y = f\left( x \right)\) có đồ thị như Hình 4. Xét tính đơn điệu và tìm các điểm cực trị của hàm số \(y = f\left( x \right)\).

Bài 30 :
Chứng minh rằng
a) \(\tan x > x\) với mọi \(x \in \left( {0;\frac{\pi }{2}} \right)\);
b) \(\ln x \le x - 1\) với mọi \(x > 0\).


















Danh sách bình luận