Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2017;2018} \right]\) để hàm số $y = \dfrac{1}{3}{x^3} - m{x^2} + \left( {m + 2} \right)x$ có hai điểm cực trị nằm trong khoảng $\left( {0; + \infty } \right)$.
-
A.
$2015.$
-
B.
$2016.$
-
C.
$2018.$
-
D.
$4035.$
Hàm số có hai điểm cực trị nằm trong khoảng \(\left( {0; + \infty } \right)\) \( \Leftrightarrow \) phương trình \(y' = 0\) có hai nghiệm dương phân biệt.
Ta có: $y' = {x^2} - 2mx + m + 2$
Yêu cầu bài toán $ \Leftrightarrow y' = 0$ có hai nghiệm dương phân biệt
$ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {m^2} - m - 2 > 0\\S = {x_1} + {x_2} > 0\\P = {x_1}{x_2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m + 1} \right)\left( {m - 2} \right) > 0\\2m > 0\\m + 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < - 1\end{array} \right.\\m > 0\end{array} \right. \Leftrightarrow m > 2$
Mà \(m \in \mathbb{Z},m \in \left[ { - 2017;2018} \right] \Rightarrow m = \left\{ {3;4;5;...2018} \right\}\)
Vậy có \(2016\) giá trị.
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
Tìm tất cả các giá trị của $m$ để hàm số $y = \dfrac{{m{x^3}}}{3} - m{x^2} + x - 1$ có cực đại và cực tiểu.
-
A.
$0 < m \leqslant 1.$
-
B.
$\left[ \begin{gathered}m < 0 \hfill \\m > 1 \hfill \\ \end{gathered} \right.$
-
C.
$0 < m < 1.$
-
D.
$m < 0.$
Bài 2 :
Hãy lập phương trình đường thẳng $(d)$ đi qua các điểm cực đại và cực tiểu của đồ thị hàm số $y = {x^3} + 3m{x^2} - 3x$
-
A.
$y = mx + 3m - 1$
-
B.
$y = - 2\left( {m^2 + 1} \right)x + m$
-
C.
$y = \left( {2{m^3} - 2} \right)x$
-
D.
$y = - 2x + 2m$
Bài 3 :
Cho hàm số $y = {x^3} + 6{x^2} + 3\left( {m + 2} \right)x - m - 6$ với \(m\) là tham số thực. Tìm tất cả các giá trị của \(m\) để hàm số có hai điểm cực trị ${x_1},{\rm{ }}{x_2}$ thỏa mãn ${x_1} < - 1 < {x_2}$.
-
A.
$m > 1$
-
B.
$m < 1$
-
C.
$m > - 1$
-
D.
$m < - 1$
Bài 4 :
Tìm tất cả các giá trị thực của tham số m để hàm số $y = {x^3} - 3{x^2} + (m + 1)x + 2$ có hai điểm cực trị.
-
A.
$m \le 2.$
-
B.
$m > 2.$
-
C.
$m < 2.$
-
D.
$m < - 4.$
Bài 5 :
Cho hàm số \(y = {x^3} - 3{x^2} - 9x + m\). Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.
-
A.
\(y = - 8x + m\).
-
B.
\(y = - 8x + m - 3\).
-
C.
\(y = - 8x + m + 3\).
-
D.
\(y = - 8x - m + 3\).
Bài 6 :
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} - {x^2} \)\(+ \left( {{m^2} - 8m + 16} \right)x - 31\) có cực trị?
Bài 7 :
Tất cả các giá trị của tham số \(m\) để hàm số \(y = \dfrac{{ - {x^3}}}{3} + m{x^2} - 2mx + 1\) có hai điểm cực trị là:
Bài 8 :
Gọi \(A\left( {{x_1};{y_1}} \right)\), \(B\left( {{x_2};{y_2}} \right)\) là hai điểm cực trị của đồ thị hàm số \(y = {x^3} - 3x - 2\). Giá trị \({y_1} + {y_2}\) bằng
-
A.
0.
-
B.
3.
-
C.
\( - 2.\)
-
D.
\( - 4.\)
Bài 9 :
Tìm cực trị của các hàm số sau:
a) \(y = {x^4} - 3{x^2} + 1\);
b) \(y = \frac{{ - {x^2} + 2x - 1}}{{x + 2}}\).
Bài 10 :
Cho hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm mà tại đó đạo hàm \(f'\left( x \right)\) bằng 0.
b) Lập bảng biến thiên của hàm số.
c) Từ bảng biến thiên suy ra các điểm cực trị của hàm số.
Bài 11 :
Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số \(N\left( t \right) = \frac{{25t + 10}}{{t + 5}},t \ge 0\), trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N’(t) và \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right)\). Từ đó giải thích tại sao dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua một ngưỡng nào đó.
Bài 12 :
Tìm cực trị của các hàm số sau:
a) \(y = 2{x^3} - 9{x^2} + 12x - 5\);\(y = {x^4} - 4{x^2} + 2\)
b) ;
c) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\);
d) \(y = \sqrt {4x - 2{x^2}} \).
Bài 13 :
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f\left( t \right) = \frac{{5\;000}}{{1 + 5{e^{ - t}}}},t \ge 0,\) trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f’(t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Bài 14 :
Hàm số nào dưới đây không có cực trị?
A. \(y = \left| x \right|\).
B. \(y = {x^4}\).
C. \(y = - {x^3} + x\).
D. \(y = \frac{{2x - 1}}{{x + 1}}\).
Bài 15 :
Giá trị cực tiểu của hàm số \(y = {x^2}\ln x\) là
A. \(\frac{1}{e}\).
B. \( - \frac{1}{e}\).
C. \( - \frac{1}{{2e}}\).
D. \(\frac{1}{{2e}}\).
Bài 16 :
Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:
a) \(y = {x^3} - 3{x^2} + 3x - 1\);
b) \(y = {x^4} - 2{x^2} - 1\);
c) \(y = \frac{{2x - 1}}{{3x + 1}}\);
d) \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).
Bài 17 :
Tìm điểm cực trị của mỗi hàm số sau:
a) \(y = {x^4} - 6{x^2} + 8x + 1\).
b) \(y = \frac{{3x + 5}}{{x - 1}}\).
Bài 18 :
Tìm cực trị của mỗi hàm số sau:
a) \(y = 2{x^3} + 3{x^2} - 36x - 10\);
b) \(y = -{x^4} - 2{x^2} + 9\);
c) \(y = x + \frac{1}{x}\).
Bài 19 :
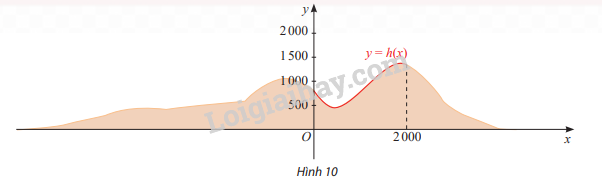
Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số \(y = h\left( x \right) = - \frac{1}{{1320000}}{x^3} + \frac{9}{{3520}}{x^2} - \frac{{81}}{{44}}x + 840\) với \(0 \le x \le 2000\)
Tìm toạ độ các đỉnh của lát cắt dãy núi trên đoạn [0; 2000]
Bài 20 :
Tìm cực trị của hàm số \(g\left( x \right) = \frac{{{x^2} + x + 4}}{{x + 1}}\)
Bài 21 :
Tìm cực trị của các hàm số sau:
a) \(y = 2{x^3} + 3{x^2}-36x + 1\)
b) \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\)
c) \(y = \sqrt { - {x^2} + 4} \)
Bài 22 :
Cho hàm số \(y = \frac{{{x^2} - 4x + 1}}{{x - 4}}\). Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 2.
B. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 6.
C. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 6.
D. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 2.
Bài 23 :
Giả sử hàm số \({x^3} - 3{x^2} + 4\) đạt cực đại tại x = a và đạt cực tiểu tại x = b. Giá trị của biểu thức a – 2b bằng bao nhiêu?
Bài 24 :
Cho hàm số y = f(x) có đạo hàm \(f'(x) = x(x - 2)({x^2} - 4)(x + 1)\). Hàm số y = f(x) có bao nhiêu điểm cực trị?
-
A.
3
-
B.
2
-
C.
4
-
D.
5
Bài 25 :
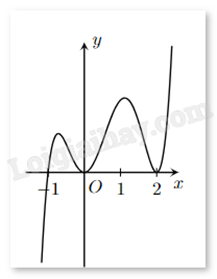
Hàm số f(x) có đạo hàm f’(x) trên khoảng K. Hình vẽ dưới là đồ thị của hàm số f’(x) trên khoảng K. Hỏi hàm số f(x) có bao nhiêu điểm cực trị?
-
A.
1
-
B.
2
-
C.
0
-
D.
3
Bài 26 :
Cho hàm số y = f(x) có đồ thị như hình:
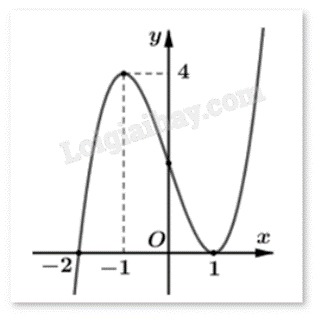
Tìm số điểm cực trị của hàm số \(g(x) = f({x^2} - 3)\).
Bài 27 :
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2}{\left( {{x^2} - 1} \right)^2}\left( {x - 2} \right),\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là:
A. 1.
B. 2.
C. 3.
D. 4.
Bài 28 :
Cho hàm số \(y = 2{x^3} + 3x + 2\). Kết luận nào sau đây là đúng?
A. Hàm số có 3 cực trị.
B. Hàm số có 2 cực trị.
C. Hàm số có 1 cực trị.
D. Hàm số không có cực trị.
Bài 29 :
Hàm số \(y = {x^3} - 3{x^2} - 9x - 3\) đạt cực tiểu tại điểm:
A. ‒1.
B. 3.
C. 2.
D. ‒30.
Bài 30 :
Tìm điểm cực trị của mỗi hàm số sau:
a) \(y = {x^3} - 12{\rm{x}} + 8\);
b) \(y = 2{{\rm{x}}^4} - 4{{\rm{x}}^2} - 1\);
c) \(y = \frac{{{x^2} - 2{\rm{x}} - 2}}{{x + 1}}\);
d) \(y = - x + 1 - \frac{9}{{x - 2}}\).


















Danh sách bình luận