Đề bài

Cho các dạng đồ thị (I), (II), (III) như hình dưới đây:

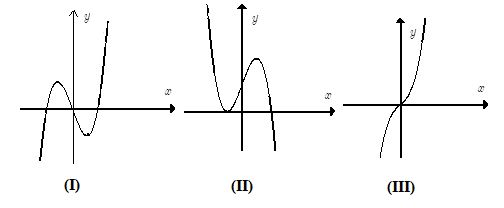
Liệt kê tất cả các dạng có thể biểu diễn đồ thị hàm số \(y = {x^3} + b{x^2} - x + d\).

• A. (I)
• B. (I) và (II)
• C. (III)
• D. (I) và (IIII)

Phương pháp giải

Nhận xét hệ số \(a\) của hàm số suy ra dáng đồ thị, tính \(y'\) suy ra số cực trị và kết luận.

Lời giải của GV Loigiaihay.com

Hàm số \(y = {x^3} + b{x^2} - x + d\) có hệ số của \({x^3}\) dương nên loại (II).

Xét \(y' = 3{x^2} + 2bx - 1\) có \(\Delta ' = {b^2} + 3 > 0,\forall b \in \mathbb{R}\).

Do đó hàm số có hai cực trị.

Đáp án : A