Đề bài

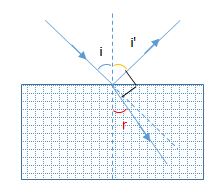
Chiếu một tia sáng đơn sắc đi từ không khí vào môi trường có chiết suất \(n\), sao cho tia phản xạ vuông góc với tia khúc xạ. Khi đó góc tới \(i\) được tính theo công thức:

• A. \(sini{\rm{ }} = {\rm{ }}n\)
• B. \(sini = \dfrac{1}{n}\)
• C. \(tani = n\)
• D. \(tani = \dfrac{1}{n}\)

Phương pháp giải

+ Sử dụng biểu thức định luật khúc xạ ánh sáng: \(\dfrac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = {n_{21}} = \dfrac{{{n_2}}}{{{n_1}}} = n\)

+ Mối quan hệ lượng giác của hai góc phụ nhau: \(i + r = {90^0} \to {\mathop{\rm sinr}\nolimits}  = c{\rm{osi}}\)

Lời giải của GV Loigiaihay.com

Ta có: tia phản xạ và tia khúc xạ vuông góc với nhau \( \to \) \(i'{\rm{  +  }}r{\rm{  =  }}{90^0}\)

Mà \(i'{\rm{  =  i}}\)\( \to \) \(i{\rm{  +  }}r{\rm{  =  }}{90^0}\)

Ta có:  

\(\dfrac{{{\rm{sin i}}}}{{{\rm{sin r}}}}{\rm{  =  }}{{\rm{n}}_{{\rm{21}}}}{\rm{ =  }}\dfrac{{{{\rm{n}}_{\rm{2}}}}}{{{{\rm{n}}_{\rm{1}}}}} = {\rm{n}}\) (1)

 \({\rm{i  +  r  =  9}}{{\rm{0}}^{\rm{0}}} \to {\rm{sin r  =  cos i}}\)(2)

\( \to \) \(tani = n\)

Đáp án : C