Đề bài

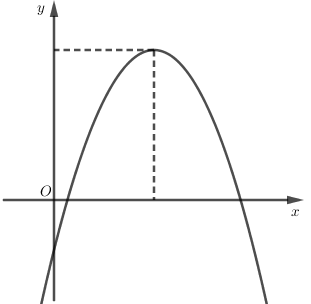
Cho hàm số $y = a{x^2} + bx + c$ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

• A. $a < 0$, $b < 0$, $c < 0$.
• B. $a < 0$, $b = 0$, $c < 0$.
• C. $a > 0$, $b > 0$, $c < 0$.
• D. $a < 0$, $b > 0$, $c < 0$.

Phương pháp giải

Quan sát đồ thị hàm số, nhận xét đỉnh parabol, dáng bề lõm và điểm đi qua, từ đó suy ra \(a,b,c\)

Lời giải của GV Loigiaihay.com

Quan sát đồ thị ta có:

Đồ thị quay bề lõm xuống dưới nên \(a < 0\); có hoành độ đỉnh \({x_I} =  - \dfrac{b}{{2a}} > 0 \Leftrightarrow \dfrac{b}{a} < 0 \Rightarrow b > 0\).

Lại có: đồ thị cắt \(Oy\) tại điểm có tung độ âm nên \(c < 0\).

Vậy $a < 0$, $b > 0$, $c < 0$.

Đáp án : D

Chú ý

Một số em có thể sẽ chọn nhầm A vì ở bước xét $ - \dfrac{b}{{2a}} > 0$ lại suy ra $b<0$ là sai.