Trên mặt nước, hai nguồn kết hợp $A, B$ cách nhau $40cm$ luôn dao động cùng pha, có bước sóng $6cm$. Hai điểm $CD$ nằm trên mặt nước mà $ABCD$ là một hình chữ nhật, $AD = 30cm$. Số điểm cực đại và đứng yên trên đoạn $CD$ lần lượt là :
-
A.
$5$ và $6$
-
B.
$7$ và $6$
-
C.
$13$ và $12$
-
D.
$11$ và $10$
Áp dụng công thức xác định cực đại trên cạnh DC của hình chữ nhật của 2 nguồn cùng pha:
\(\dfrac{{AD - BD}}{\lambda } < k < \dfrac{{AC - BC}}{\lambda }\)
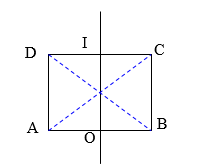
\(BD = AD = \sqrt {A{B^2} + A{D^2}} = 50cm\)
Cách 1 :
Bước 1: Số điểm cực đại trên đoạn $DI$ thoã mãn :
\({d_2} - {d_1} = k\lambda \Rightarrow k = \dfrac{{{d_2} - {d_1}}}{\lambda } = \dfrac{{BD - AD}}{\lambda } = \dfrac{{50 - 30}}{6} = 3,33\) Với k thuộc $Z$ lấy $k=3$
Vậy số điểm cực đại trên đoạn $CD$ là : $k’=2.k + 1=3.2 + 1=7$
Bước 2 : Số điểm cực tiểu trên đoạn $DI$ thoã mãn :
\({d_2} - {d_1} = (2k + 1)\dfrac{\lambda }{2} \Rightarrow 2k + 1 = \dfrac{{2({d_2} - {d_1})}}{\lambda } = \dfrac{{2(BD - AD)}}{\lambda } = \dfrac{{2(50 - 30)}}{6} = 6,67\) .
Giải suy ra $k = 2,83$ (Với k thuộc Z) nên lấy $k=3$ ( vì \(k = 2,83 > 2,5\) ta lấy cận trên là $3$)
Vậy số điểm cực tiểu trên đoạn $CD$ là : $k’ = 2.k = 2.3 = 6$
Cách 2 :
Do hai nguồn dao động cùng pha nên số điểm dao động với biên độ cực đại trên đoạn $CD$ thoã mãn :
Số điểm cực đại trên đoạn $CD$ thoã mãn :
\(\left\{ \begin{array}{l}{d_2} - {d_1} = k\lambda \\AD - BD < {d_2} - {d_1} < AC - BC\end{array} \right.\)
Suy ra :
\(AD - BD < k\lambda < AC - BC\) Hay : \(\dfrac{{AD - BD}}{\lambda } < k < \dfrac{{AC - BC}}{\lambda }\). Hay : \(\dfrac{{30 - 50}}{6} < k < \dfrac{{50 - 30}}{6}\)
Giải ra : $-3,3<k<3,3$
Kết luận có $7$ điểm cực đại trên $CD$.
Số điểm cực tiểu trên đoạn $CD$ thoã mãn :
\(\left\{ \begin{array}{l}{d_2} - {d_1} = (2k + 1)\dfrac{\lambda }{2}\\AD - BD < {d_2} - {d_1} < AC - BC\end{array} \right.\)
Suy ra :
\(AD - BD < (2k + 1)\dfrac{\lambda }{2} < AC - BC\) Hay : \(\dfrac{{2(AD - BD)}}{\lambda } < 2k + 1 < \dfrac{{2(AC - BC)}}{\lambda }\). Thay số :
\(\dfrac{{2(30 - 50)}}{6} < 2k + 1 < \dfrac{{2(50 - 30)}}{6}\) Suy ra : \( - 6,67 < 2k + 1 < 6,67\)
Vậy : $-3,8 < k < 2,835$. Kết luận có 6 điểm đứng yên.
Đáp án : B

Các bài tập cùng chuyên đề


















Danh sách bình luận