Đề bài

Ở mặt nước, tại hai điểm \({S_1}\) và \({S_2}\) có hai nguồn dao động cùng pha theo phương thẳng đứng, phát ra hai sóng kết hợp có bước sóng \(\lambda \). Cho \({S_1}{S_2} = {\rm{ }}5,4\lambda \). Gọi (C) là hình tròn nằm ở mặt nước có đường kính là \({S_1}{S_2}\). Số vị trí trong (C) mà các phần tử ở đó dao động với biên độ cực đại và cùng pha với dao động của các nguồn là :

• A. 18
• B. 9
• C. 22
• D. 11

Phương pháp giải

+ Sử dụng điều kiện dao động cực đại trong giao thoa của hai nguồn cùng pha : \({d_2} - {d_1} = k\lambda \)

+ Sử dụng định lí hàm số cos trong tam giác

Lời giải của GV Loigiaihay.com

Điều kiện để điểm dao động với biên độ cực đại trong giao thoa hai nguồn cùng pha là \({d_2} - {d_1} = k\lambda \)

- Áp dụng định lí hàm cos trong tam giác

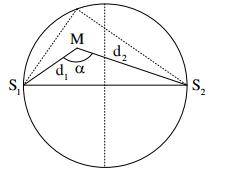
Gọi M là một điểm bất kỳ trên nửa phía trên.

- Để tại M các phần tử nước dao động với biên độ cực đại và cùng pha với nguồn thì sóng do hai nguồn truyền tới M phải cùng pha với nhau và cùng pha với nguồn, suy ra M phải cách các nguồn một số nguyên lần bước sóng

\(\left\{ \begin{array}{l}{d_1} = {k_1}\lambda \\{d_2} = {k_2}\lambda \end{array} \right.\)

Để M nằm bên trong đường tròn (C) thì \(\alpha  > {90^0} =  > \cos \alpha  < 0\)

Áp dụng định lý hàm cos cho tam giác MS­₁S₂ ta có :

\(\begin{array}{l}\cos \alpha  = \frac{{d_1^2 + d_2^2 - {{\left( {{S_1}{S_2}} \right)}^2}}}{{2{d_1}{d_2}}} = \frac{{k_1^2 + k_2^2 - {{5,4}^2}}}{{2{k_1}{k_2}}}\\\cos \alpha  < 0 =  > k_1^2 + k_2^2 < {5,4^2} = 29,16\\ =  > \left| {{d_1} - {d_2}} \right| < {S_1}{S_2} < {d_1} + {d_2} =  > \left| {{k_1} - {k_2}} \right| < 5,4 \le {k_1} + {k_2}\end{array}\)

Vậy có tất cả 9 điểm

=> Tính thêm nửa dưới ta có 18 điểm

Đáp án : A