Vận tốc của vật dao động điều hoà có phương trình li độ $x = A\cos \left( {\omega t - \dfrac{\pi }{3}} \right)$ có độ lớn cực đại khi:
Vận tốc của vật dao động điều hoà có phương trình li độ $x = A\cos \left( {\omega t - \dfrac{\pi }{3}} \right)$ có độ lớn cực đại khi:
-
A.
$t = 0$
-
B.
$t = \frac{T}{4}$
-
C.
$t = \frac{T}{{12}}$
-
D.
$t = \frac{{5T}}{{12}}$
+ Vận tốc của vật có độ lớn cực đại khi vật ở VTCB
+ Xác định li độ và chiều của vận tốc tại thời điểm ban đầu $t = 0$
+ Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn
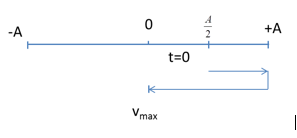
Ta có, vận tốc của vật có độ lớn cực đại khi vật ở VTCB
Tại thời điểm ban đầu t =0 : \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\left( { - \dfrac{\pi }{3}} \right) = \dfrac{A}{2}\\v = - A\omega \sin \left( { - \dfrac{\pi }{3}} \right) > 0\end{array} \right.\)
=> Vận tốc của vật có độ lớn cực đại khi \(t = \dfrac{T}{6} + \dfrac{T}{4} = \dfrac{{5T}}{{12}}\)
Đáp án : D
Các bài tập cùng chuyên đề
Gia tốc của một vật dao động điều hoà có phương trình li độ $x = A\cos \left( {\omega t - \dfrac{{5\pi }}{6}} \right)$ có độ lớn cực đại. Khi:
Một vật dao động điều hòa với biên độ $A$ quanh vị trí cân bằng $0$, thời gian ngắn nhất để vật di chuyển từ vị trí có ly độ $x = - \dfrac{A}{2}$ đến vị trí có ly độ $x = A$ là $\dfrac{1}{2}s$, chu kỳ dao động:
Vật dao động điều hòa theo phương trình: \(x = 5c{\rm{os}}\left( {2\pi t - \frac{\pi }{3}} \right)cm\). Xác định thời gian ngắn nhất kể từ khi vật bắt đầu chuyển động đến vị trí có li độ \(x = \frac{{5\sqrt 2 }}{2}\) lần thứ nhất?
Một chất điểm dao động điều hòa với chu kì $T$ và biên độ $5cm$. Biết trong một chu kì, khoảng thời gian để vật nhỏ của chất điểm có độ lớn gia tốc không vượt quá $100cm/{s^2}$ là \(\dfrac{T}{3}\). Lấy ${\pi ^2} = 10$. Tần số dao động của vật là:
Một chất điểm đang dao động điều hòa trên một đoạn thẳng xung quanh vị trí cân bằng O. Gọi M, N là hai điểm trên đường thẳng cùng cách đều O. Biết cứ $0,05s$ thì chất điểm lại đi qua các điểm M, O, N và tốc độ của nó đi qua vị trí M, N là $20\pi \left( {cm/s} \right)$. Biên độ A bằng.
Một vật nhỏ dao động điều hòa với chu kì $T$ và biên độ $8 cm$. Biết trong một chu kì, khoảng thời gian để vật nhỏ có độ lớn vận tốc không vượt quá $16 cm/s$ là $\dfrac{T}{3}$. Tần số góc của dao động là:
Một vật dao động điều hòa theo phương trình \(x = 8c{\rm{os}}\left( {2\pi t + \dfrac{\pi }{6}} \right)cm\). Xác định thời gian vật chuyển động từ thời điểm $t=0,75s$ đến khi vật có li độ $x=-4 cm$ lần thứ $2$?
Một vật dao động được kích thích để dao động điều hòa với vận tốc cực đại bằng $3 m/s$ và gia tốc cực đại bằng $30\pi m/{s^2}$. Thời điểm ban đầu $t = 0$ vật có vận tốc $v=+1,5 m/s$ và thế năng đang tăng. Hỏi sau đó bao lâu vật có gia tốc bằng $ - 15\pi m/{s^2}$
Một chất điểm dao động điều hòa theo phương trình \(x = 4c{\rm{os}}\left( {\dfrac{{2\pi }}{3}t} \right)cm\)(x tính bằng cm, t tính bằng giây). Kể từ $t=0$, chất điểm đi qua vị trí có li độ $x= -2cm$ lần thứ $2011$ tại thời điểm:
Một vật dao động điều hòa với phương trình: \(x = 10c{\rm{os}}\left( {20\pi t - \dfrac{\pi }{6}} \right)cm\). Xác định thời điểm thứ $2016$ vật có gia tốc bằng không?
Một vật dao động điều hòa với phương trình: \(x = 8c{\rm{os}}\left( {2\pi t - \dfrac{\pi }{6}} \right)cm\). Thời điểm lần thứ $2010$ kể từ lúc bắt đầu dao động, vật qua vị trí có vận tốc $v= -8π cm/s$ là bao nhiêu?
Một vật dao động điều hòa với phương trình: \(x = 6c{\rm{os}}\left( {4\pi t + \frac{\pi }{4}} \right)cm\). Khoảng thời gian vật qua vị trí có li độ \(x = 3\sqrt 2 cm\) theo chiều dương lần thứ $2017$ kể từ lúc $t=0,125s$ là?
Một vật dao động theo phương trình \(x = 3\cos \left( {5\pi t - \frac{{2\pi }}{3}} \right)cm\). Trong giây đầu tiên vật qua vị trí cân bằng bao nhiêu lần?
Một chất điểm dao động điều hòa theo phương trình \(x = 3\sin \left( {5\pi t + \frac{\pi }{6}} \right)cm\) (x tính bằng cm, t tính bằng giây). Trong một giây đầu tiên từ thời điểm $t = 0,4s$, chất điểm đi qua vị trí có li độ $x = + 1 cm$
Một vật dao động điều hoà với phương trình \(x = 8\cos \left( {2\pi t - \frac{\pi }{3}} \right)cm\). Tìm số lần vật qua vị trí có vận tốc \(v = - 8\pi \left( {cm/s} \right)\) trong thời gian $5,75s$ tính từ thời điểm gốc.
Một vật dao động điều hoà với phương trình $x = 4c{\rm{os}}\left( {4\pi t + \dfrac{\pi }{6}} \right)cm$. Tìm số lần vật qua vị trí có gia tốc là $32{\pi ^2}cm/{s^2}$ theo chiều dương trong thời gian $5,75s$ tính từ thời điểm gốc.
Hai điểm sáng cùng dao động trên trục Ox với các phương trình li độ lần lượt là \({x_1} = Acos\left( {2\pi t + \dfrac{\pi }{6}} \right)\) ; \({x_2} = Acos\left( {2\pi t + \dfrac{{5\pi }}{6}} \right)\). Thời điểm mà hai điểm sáng có cùng li độ lần thứ 2020 là
