Tia phân giác góc \(\widehat {BAD}\) của hình bình hành \(ABCD\) cắt các đường thẳng \(BC\) và \(DC\) lần lượt tại hai điểm \(M\) và \(N.\) Dựng ra phía ngoài hình bình hành \(ABCD\) tam giác \(MCO\) cân tại $O$ với \(\widehat {MOC} = \widehat {BAD}\). Khi đó:
-
A.
\(B,O,C,D\) thuộc cùng một đường tròn
-
B.
\(B,O,C,D\) không thuộc cùng một đường tròn
-
C.
Cả \(A,B\) đều đúng
-
D.
Cả \(A,B\) đều sai
Sử dụng dấu hiệu hai đỉnh kề nhau cùng nhìn cạnh đối diện các góc bằng nhau thì tứ giác đó là tứ giác nội tiếp.
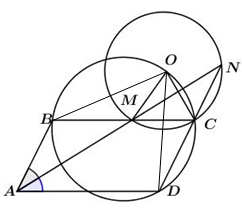
Ta có \(BM//AD\) nên \(\widehat {BMA} = \widehat {MAD}.\)
Mặt khác \(AM\) là phân giác của \(\widehat {BAD}\) nên \(\widehat {BAM} = \widehat {MAD}.\)
Từ đó \(\widehat {BAM} = \widehat {AMB.}\)
Vậy \(\Delta ABM\) cân tại \(B.\) Suy ra \(BM = BA = DC.\)
Tam giác \(OMC\) cân tại \(O\) nên \(OM = OC\) và \(\widehat {OMC} = \widehat {OCM} \)\(= \dfrac{{180^\circ - \widehat {MOC}}}{2} \)\(= \dfrac{1}{2}\left( {180^\circ - \alpha } \right)\)
Đặt \(\alpha = \widehat {BAD},\) ta có \(\widehat {OCD} \)\(= \widehat {BCD} + \widehat {OCM} \)\(= \alpha + \dfrac{1}{2}\left( {{{180}^0} - \alpha } \right) \)\(= {90^0} + \dfrac{\alpha }{2}\,\,\left( 1 \right).\)
Các góc \(\widehat {BMO},\,\widehat {OMC}\) kề bù nên
\(\widehat {BMO} = {180^0} - \,\widehat {OMC} = {180^0} - \,\widehat {OCM} = {90^0} + \dfrac{\alpha }{2}\,\,\left( 2 \right).\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {OCD} = \widehat {BMO}.\)
Xét hai tam giác \(\Delta OBM,\,\Delta ODC\) có \(\left\{ \begin{array}{l}\widehat {OCD} = \widehat {BMO}\\OM = OC \, (cmt)\\BM = CD \, (cmt)\end{array} \right.\) nên \(\Delta OBM = \Delta ODC\,\,\left( {c.g.c} \right).\)
Do đó \(\widehat {OBM} = \widehat {ODC}.\) Điều này chứng tỏ \(BOCD\) là tứ giác nội tiếp. Do đó bốn điểm \(B,\,O,\,C,\,D\) thuộc cùng một đường tròn.
Đáp án : A

Các bài tập cùng chuyên đề

















