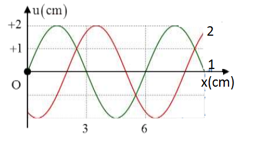
Một sóng cơ lan truyền dọc theo trục Ox với phương trình có dạng \(u = ac{\rm{os}}\left( {\frac{{2\pi }}{T}t - \frac{{2\pi x}}{\lambda }} \right)\). Trên hình vẽ đường (1) là hình dạng của sóng ở thời điểm t, đường (2) là hình dạng của sóng ở thời điểm trước đó \(\frac{1}{{12}}s\). Phương trình sóng là:
-
A.
\(u = 2c{\rm{os}}\left( {10\pi t - \frac{{2\pi x}}{3}} \right)cm\)
-
B.
\(u = 2c{\rm{os}}\left( {8\pi t - \frac{{\pi x}}{3}} \right)cm\)
-
C.
\(u = 2c{\rm{os}}\left( {10\pi t + \frac{{\pi x}}{3}} \right)cm\)
-
D.
\(u = 2c{\rm{os}}\left( {10\pi t - 2\pi x} \right)cm\)
+ Sử dụng phương pháp đọc đồ thị dao động sóng
+ Sử dụng các công thức: \(\Delta \varphi = \omega \Delta t\)
+ Sử dụng vòng tròn lượng giác
Từ đồ thị dao động sóng, ta có:
\(\frac{\lambda }{2} = 6 - 3 = 3 \to \lambda = 6cm\) ; biên độ sóng a = 2cm
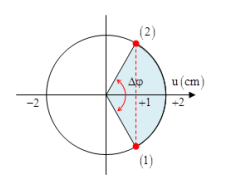
Tại cùng một vị trí trong không gian, ở hai thời điểm t1 và t2 phần tử môi trường đều có li độ là 1cm nhưng di chuyển theo 2 chiều ngược nhau, ta có:
\(\Delta \varphi = \omega \Delta t \leftrightarrow \frac{{2\pi }}{3} = \omega \frac{1}{{12}} \to \omega = 8\pi ra{\rm{d}}/s\)
\( \to u = 2c{\rm{os}}\left( {8\pi t - \frac{{\pi x}}{3}} \right)cm\)
Đáp án : B
Các bài tập cùng chuyên đề
