Đề bài

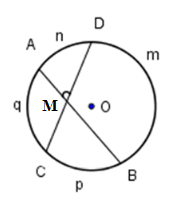
Cho hình vẽ ở bên. Khi đó mệnh đề đúng là:

• A. \(\widehat {AMD} = \)\(\dfrac{1}{2}\) ( sđ\( \overparen{AnD} + \) sđ\(\overparen{CpB}\))
• B. \(\widehat {AMD} = \) $\dfrac{1}{2}$ ( sđ\(\overparen{AqC}+ \) sđ\(\overparen{DmB}\) )
• C. \(\widehat {AMD} = \)\(\dfrac{1}{2}\) (  sđ\(\overparen{AnD} - \) sđ\(\overparen{CpB}\))
• D. \(\widehat {AMD} = \)$\dfrac{1}{2}$ ( sđ\(\overparen{AqC} - \) sđ\(\overparen{DmB}\))

Phương pháp giải

Tính chất góc có đỉnh nằm trong đường tròn: Số đo góc có đỉnh nằm trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn.

Lời giải của GV Loigiaihay.com

Góc \(\widehat {AMD}\) là góc có đỉnh bên trong đường tròn chắn cung \(AD\) và cung \(BC\) nên ta có

\(\widehat {AMD} = \)\(\dfrac{1}{2}\) ( sđ\(\overparen{AnD} + \) sđ\(\overparen{CpB}\))

Đáp án : A