Hai điểm M, N cùng nằm trên một phương truyền sóng cách nhau λ/3. Tại thời điểm t, khi li độ dao động tại M là uM = + 3 cm thì li độ dao động tại N là uN = - 3 cm. Biên độ sóng bằng :
-
A.
\(A = \sqrt 6 cm\)
-
B.
A = 3 cm.
-
C.
\(A = 2\sqrt 3 cm\)
-
D.
\(A = 3\sqrt 3 cm\).
Áp dụng biểu thức xác định độ lệch pha: \(\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda }\)
+ Cách 1: Dùng phương trình sóng
Viết phương trình sóng tại M và N
Áp dụng công thức lượng giác: \({\rm{cosa + cosb}} = 2c{\rm{os}}\frac{{a + b}}{2}{\rm{cos}}\frac{{a - b}}{2}\)
+ Cách 2: Sử dụng vòng tròn lượng giác
Ta có: Độ lệch pha giữa hai điểm MN là: \(\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda } = \frac{{2\pi \frac{\lambda }{3}}}{\lambda } = \frac{{2\pi }}{3}\)
Giả sử dao động tại M sớm pha hơn dao động tại N.
Cách 1: Dùng phương trình sóng
Ta có thể viết:
\(\begin{array}{l}{u_M} = Ac{\rm{os}}\omega t = + 3cm{\rm{ (1)}}\\{u_N} = Ac{\rm{os}}\left( {\omega t - \frac{{2\pi }}{3}} \right) = - 3cm{\rm{ (2)}}\end{array}\)
Lấy (1) + (2), ta được:
\(\begin{array}{l}{u_M} + {u_N} = 0 = Ac{\rm{os}}\omega t + Ac{\rm{os}}\left( {\omega t - \frac{{2\pi }}{3}} \right)\\ \leftrightarrow 2Ac{\rm{os}}\frac{\pi }{3}{\rm{cos}}\left( {\omega t - \frac{\pi }{3}} \right) = 0 \to \omega t - \frac{\pi }{3} = \frac{\pi }{2} + k\pi \\ \to \omega t = \frac{{5\pi }}{6} + k\pi \end{array}\)
Thay vào (1), ta được:
\(Ac{\rm{os}}\left( {\frac{{5\pi }}{6} + k\pi } \right) = 3\)
Do A > 0,
\(Ac{\rm{os}}\left( {\frac{{5\pi }}{6} - \pi } \right) = 3 \to Ac{\rm{os}}\left( { - \frac{\pi }{6}} \right) = 3 \to A = 2\sqrt 3 cm\)
=> Chọn C
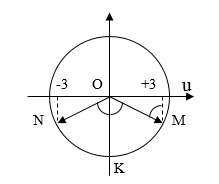
Cách 2: Sử dụng vòng tròn lượng giác
Xác định tọa độ N, M trên vòng tròn lượng giác, ta được:
Từ vòng tròn lượng giác, ta có:
\(\begin{array}{l}\angle NOK = \angle KOM = \frac{{\Delta \varphi }}{2} = \frac{\pi }{3}\\ \to {\rm{A}}\sin \frac{\pi }{3} = 3cm \to A = 2\sqrt 3 cm\end{array}\)
Đáp án : C
Các bài tập cùng chuyên đề
Sóng truyền từ $O$ đến $M$ với vận tốc $v = 40cm/s$, phương trình sóng tại $O$ là \({u_0} = 4sin\dfrac{\pi }{2}t\left( {cm} \right)\). Biết vào thời điểm $t$ thì li độ của phần tử $M$ là $3cm$ và đang chuyển động theo chiều dương, vậy lúc $t + 6(s)$ li độ của $M$ là:
Một sóng cơ lan truyền trên một sợi dây rất dài có phương trình \(u = 6\cos \left( {4\pi t - 0,02\pi x} \right)\); trong đó u và x có đơn vị là cm, t có đơn vị là giây. Hãy xác định li độ dao động của một điểm trên dây có toạ độ x = 25 cm tại thời điểm t = 4 s.
Một sóng cơ học lan truyền trên mặt nước với tốc độ 25cm/s. Phương trình sóng tại nguồn là u = 3cosπt(cm). Vận tốc của phần tử vật chất tại điểm M cách O một khoảng 25cm tại thời điểm t = 2,5s là:
Nguồn sóng ở O dao động với tần số 10Hz, dao động truyền đi với vận tốc 0,4m/s theo phương Oy; trên phương này có hai điểm P và Q với PQ = 15cm. Biên độ sóng bằng a = 1cm và không thay đổi khi lan truyền . Nếu tại thời điểm t nào đó P có li độ 1cm thì li độ tại Q là:
Sóng có tần số \(20Hz\) truyền trên chất lỏng với tốc độ \(200cm/s\), gây ra các dao động theo phương thẳng đứng của các phần tử chất lỏng. Hai điểm M và N thuộc mặt chất lỏng cùng phương truyền sóng cách nhau \(22,5cm\). Biết điểm M nằm gần nguồn sóng hơn. Tại thời điểm t điểm N hạ xuống thấp nhất. Hỏi sau đó thời gian ngắn nhất là bao nhiêu thì điểm M sẽ hạ xuống thấp nhất?
Sóng truyền theo phương ngang trên một sợi dây dài với tần số $10Hz$. Điểm $M$ trên dây tại một thời điểm đang ở vị trí cao nhất và tại thời điểm đó điểm $N$ cách $M$ $5cm$ đang đi qua vị trí có li độ bằng nửa biên độ và đi lên. Coi biên độ sóng không đổi khi truyền. Biết khoảng cách $MN$ nhỏ hơn bước sóng của sóng trên dây. Chọn đáp án đúng cho tốc độ truyền sóng và chiều truyền sóng.
Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình sóng tại nguồn O là:
\({u_O} = A\sin (\frac{{2\pi }}{T}t)(cm).\) Một điểm M cách nguồn O bằng \(\frac{1}{3}\) bước sóng ở thời điểm \(t = \frac{T}{2}\) có ly độ \({u_M} = 2(cm).\) Biên độ sóng A là:
Một sóng cơ lan truyền từ nguồn O, dọc theo trục Ox với biên độ sóng không đổi, chu kì sóng T và bước sóng \(\lambda \). Biết rằng tại thời điểm t = 0, phần tử tại O qua vị trí cân bằng theo chiều dương và tại thời điểm t = \(\frac{{5T}}{6}\) phần tử tại điểm M cách O một đoạn d = \(\frac{\lambda }{6}\) có li độ là -2 cm. Biên độ sóng là :
Trên một sợi dây dài vô hạn có một sóng cơ lan truyền theo phương Ox với phương trình sóng u = 2cos(10πt - πx) (cm) ( trong đó t tính bằng s; x tính bằng m). M, N là hai điểm nằm cùng phía so với O cách nhau 5 m. Tại cùng một thời điểm khi phần tử M đi qua vị trí cân bằng theo chiều dương thì phần tử N
Cho phương trình sóng: $u = a\sin \left( {0,4\pi x + 7\pi t + \dfrac{\pi }{3}} \right)\left( {m,s} \right)$. Phương trình này biểu diễn:
Một nguồn O dao động với tần số f = 50Hz tạo ra sóng trên mặt nước có biên độ 3cm (coi như không đổi khi sóng truyền đi). Chọn t = 0 là lúc phần tử nước tại O đi qua vị trí cân bằng theo chiều dương. Tại thời điểm t1 li độ dao động tại M bằng 2cm. Li độ dao động tại M vào thời điểm t2 = (t1 + 2,01)s bằng bao nhiêu ?
Một sóng cơ lan truyền trên một sợi dây rất dài với biên độ không đổi, ba điểm A, B và C nằm trên sợi dây sao cho B là trung điểm của AC. Tại thời điểm t1, li độ của ba phần tử A, B, C lần lượt là – 4,8mm; 0 mm; 4,8 mm. Nếu tại thời điểm t2, li độ của A và C đều bằng +5,5 mm, thì li độ của phần tử tại B là:
Một sợi dây đàn hồi nằm ngang có điểm đầu O dao động theo phương thẳng đứng với biên độ A = 5cm, T = 0,5s. Vận tốc truyền sóng là 40cm/s. Viết phương trình sóng tại M cách O d = 50 cm.
Một sóng cơ học truyền theo phương $Ox$ với biên độ coi như không đổi. Tại $O$, dao động có dạng $u = acosωt (cm)$. Điểm M cách xa tâm dao động O là \(\dfrac{1}{3}\) bước sóng ở thời điểm bằng $0,5$ chu kì thì ly độ sóng có giá trị là $5 cm$. Phương trình dao động ở M thỏa mãn hệ thức nào sau đây:
Một dao động lan truyền trong môi trường từ điểm $N$ đến điểm $M$ cách $N$ một đoạn $0,9 (m)$ với vận tốc $1,2 (m/s)$. Biết phương trình sóng tại $N$ có dạng $u_N = 0,02cos 2πt(m)$. Viết biểu thức sóng tại $M$ :
Một sóng cơ học lan truyền trên một phương truyền sóng với vận tốc $5m/s$. Phương trình sóng của một điểm O trên phương truyền đó là:\({u_O} = 6c{\rm{os}}\left( {5\pi t + \dfrac{\pi }{2}} \right)\). Phương trình sóng tại M nằm trước O và cách O một khoảng $50cm$ là:
Sóng truyền từ điểm M đến điểm O rồi đến điểm N trên cùng một phương truyền sóng với tốc độ \(v = 20m/s\). Cho biết tại O dao động có phương trình \({u_O} = 4cos\left( {2\pi f - \dfrac{\pi }{2}} \right)cm\) và tại hai điểm gần nhau nhất cách nhau \(6m\) trên cùng phương truyền sóng thì dao động lệch pha nhau góc \(\dfrac{{2\pi }}{3}rad\). Cho \(ON = 50cm\). Phương trình sóng tại N là
Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình dao động tại nguồn O là \({u_O} = A.\cos \left( {\dfrac{{2\pi t}}{T}} \right)cm\). Một điểm M trên đường thẳng, cách O một khoảng bằng \(\dfrac{1}{3}\) bước sóng ở thời điểm \(t = \dfrac{T}{2}\) có li độ uM = 2cm. Biên độ sóng A bằng:
