Đề bài

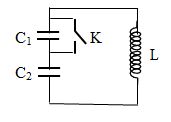
Một mạch dao động gồm cuộn thuần cảm \(L\) và hai tụ \({C_1} = 2{C_2}\) mắc nối tiếp. Mạch đang hoạt động thì ta đóng khóa \(K\) ngay tại thời điểm năng lượng trong cuộn cảm triệt tiêu. Năng lượng toàn phần của mạch sau đó sẽ:

• A. không đổi   
• B. giảm còn \(\frac{1}{3}\)    
• C. giảm còn \(\frac{2}{3}\)        
• D. giảm còn \(\frac{4}{9}\)

Phương pháp giải

Sử dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \frac{1}{2}C{U_0}^2 = \frac{{{Q_0}^2}}{{2C}} = \frac{{LI{{_0^{}}^2}}}{2}\)

Lời giải của GV Loigiaihay.com

Gọi \({Q_0}\) là điện tích cực đại trong mạch

+ Năng lượng ban đầu của mạch: \({{\rm{W}}_0} = \frac{{Q_0^2}}{{2C}} = \frac{{3Q_0^2}}{{2{C_1}}} = \frac{{3Q_0^2}}{{4{C_2}}}\)

Khi năng lượng cuộn cảm triệt tiêu: \(q{\rm{ }} = {\rm{ }}{Q_0}\)

\({W_0} = {\rm{ }}{W_1} + {\rm{ }}{W_2}\) với  \({W_2} = \frac{{Q_0^2}}{{2{C_2}}}\).

+ Khi đóng khóa K thi năng lượng toàn phấn của mạch \(W = {W_2} = \frac{{Q_0^2}}{{2{C_2}}}\) (2)

Từ đó suy ra   \(\frac{W}{{{W_0}}} = \frac{2}{3} \to {\rm{W}} = \frac{2}{3}{{\rm{W}}_0}\)

Đáp án : C