Đề bài

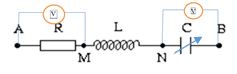
Cho mạch điện xoay chiều như hình vẽ. Điện dung \(C\) có giá trị thay đổi được và cuộn dây thuần cảm. Điều chỉnh giá trị của \(C\) thì thấy: ở cùng thời điểm, số chỉ của \({V_1}\)  cực đại (\({U_{A{M_{{\rm{max}}}}}}\)) thì số chỉ của \({V_1}\) gấp đôi số chỉ của \({V_2}\) . Hỏi khi số chỉ của \({V_2}\) cực đại ( \({U_{N{B_{{\rm{max}}}}}}\) ) thì số chỉ của \({V_2}\) gấp bao nhiêu lần số chỉ \({V_1}\)? (\({V_1}\) chỉ điện áp trên \(R\), còn \({V_2}\) chỉ điện áp trên \(C\))

• A. \(1,5\) lần
• B. \(2\) lần
• C. \(2,5\) lần
• D. \(2\sqrt 2 \)lần

Phương pháp giải

Áp dụng các tính toán đại số tìm điều kiện cực đại của điện áp khi tụ \(C\) thay đổi

+ C thay đổi để \({U_{{R_{{\rm{max}}}}}}\) khi đó mạch cộng hưởng

+ C thay đổi để \({U_{{C_{{\rm{max}}}}}}\) khi đó: \({U_{{C_{{\rm{max}}}}}} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{R}\)

Lời giải của GV Loigiaihay.com

Khi \({V_1}\) đạt cực đại thì xảy ra cộng hưởng điện:  \({U_{1\max }} = {U_R} = {U_{AB}}{\rm{ }} \Leftrightarrow {U_L} = {U_C}_1 = \frac{1}{2}{U_{AB}} =  > R = 2{Z_L} = 2{Z_{C1}}\)

Thay đổi để điện áp trên tụ cực đại thì

\(\begin{array}{l}{U_{C\max }} = \frac{U}{R}.\sqrt {{R^2} + Z_L^2} khi{Z_C} = \frac{{{R^2} + Z_L^2}}{{{Z_L}}}\\I' = \frac{{{U_{C2}}}}{{{Z_{C2}}}} = \frac{{\frac{U}{R}.\sqrt {{R^2} + Z_L^2} }}{{\frac{{{R^2} + Z_L^2}}{{{Z_L}}}}} = \frac{{U.{Z_L}}}{{R.\sqrt {{R^2} + Z_L^2} }} =  > {U_R}^\prime  = I'.R = \frac{{U.{Z_L}}}{{\sqrt {{R^2} + Z_L^2} }} = \frac{U}{{\sqrt 5 }}V\\{U_{C\max }} = \frac{U}{R}.\sqrt {{R^2} + Z_L^2}  = \frac{{U.\sqrt {4Z_L^2 + Z_L^2} }}{{2{Z_L}}} = \frac{{U.\sqrt 5 }}{2}V =  > \frac{{{U_{C\max }}}}{{{U_R}^\prime }} = \frac{{\sqrt 5 }}{2}.\sqrt 5  = 2,5\end{array}\)

Đáp án : C