Đề bài

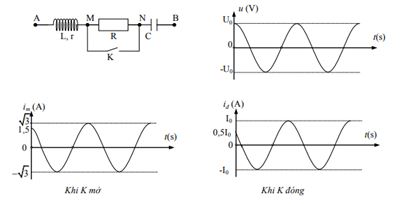
Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều có đồ thị điện áp tức thời phụ thuộc vào thời gian như hình vẽ. Trong đó điện áp cực đại \({U_0}\) và chu kì dòng điện không thay đổi. Khi đóng và mở khóa K thì cường độ dòng điện tức thời trong mạch phụ thuộc vào thời gian như hình vẽ. Giá trị của \({I_0}\)  là:

• A. \(3\sqrt 3 A\)
• B. \(3A\)
• C. \(1,5\sqrt 3 A\)
• D. \(2\sqrt 3 A\)

Phương pháp giải

+ Sử dụng định luật Ôm

+ Sử dụng công thức: \(\tan \varphi  = \frac{{{Z_L} - {Z_C}}}{R}\)

Lời giải của GV Loigiaihay.com

+ Khi khóa K mở, mạch gồm \(R,{\rm{ }}r,{\rm{ }}L,{\rm{ }}C\) nối tiếp

Từ đồ thị của điện áp, ta có: \(u = {U_0}.cos\omega t\)

Từ đồ thị cường độ dòng điện khi K mở ta có phương trình cường độ dòng điện là: \(i = {I_0}cos\left( {\omega t + {\varphi _i}_1} \right)\)

Khi \(t{\rm{ }} = {\rm{ }}0\):

\(\begin{array}{*{20}{l}}{i = 1,5 = \sqrt 3 .\cos {\varphi _{i1}} \Rightarrow {\varphi _{i1}} = \frac{\pi }{6} \Rightarrow \Delta {\varphi _m} = {\varphi _u} - {\varphi _{i1}} = \frac{{ - \pi }}{6}}\\{ \Rightarrow \tan \Delta {\varphi _m} = \frac{{{Z_L} - {Z_C}}}{{R + r}} = \frac{{ - 1}}{{\sqrt 3 }} \Rightarrow {Z_L} - {Z_C} = \frac{{ - 1}}{{\sqrt 3 }}(R + r)}\end{array}\)

+ Khi K đóng, mạch có \(r,{\rm{ }}L,{\rm{ }}C\) nối tiếp

Ta có phương trình cường độ dòng điện là: \(i = {I_0}.cos\left( {\omega t + {\varphi _{i2}}} \right)\)

Khi \(t{\rm{ }} = {\rm{ }}0\): 

\(\begin{array}{*{20}{l}}{i = 0,5{I_0} = {I_0}.\cos {\varphi _{i2}} \Rightarrow {\varphi _{i2}} = \frac{\pi }{3} \Rightarrow \Delta {\varphi _m} = {\varphi _u} - {\varphi _{i1}} = \frac{{ - \pi }}{3}}\\\begin{array}{l} \Rightarrow \tan \Delta {\varphi _m} = \frac{{{Z_L} - {Z_C}}}{r} =  - \sqrt 3  \Rightarrow {Z_L} - {Z_C} =  - \sqrt 3 r\\ \Rightarrow {Z_L} - {Z_C} =  - \sqrt 3 r = \frac{{ - 1}}{{\sqrt 3 }}(R + r) \Rightarrow R = 2r\end{array}\\{ \Rightarrow \left\{ \begin{array}{l}{Z_2} = \sqrt {{r^2} + {{({Z_L} - {Z_C})}^2}}  = 2r\\{Z_1} = \sqrt {{{(R + r)}^2} + {{({Z_L} - {Z_C})}^2}}  = 2\sqrt 3 r\end{array} \right.}\\{{I_{01}} = \frac{{{U_0}}}{{{Z_1}}};{I_{02}} = \frac{{{U_0}}}{{{Z_2}}} \Rightarrow \frac{{{I_{01}}}}{{{I_{02}}}} = \frac{{{Z_2}}}{{{Z_1}}} = \frac{1}{{\sqrt 3 }} \Rightarrow {I_{02}} = {I_0} = 3A}\end{array}\)

Đáp án : B