Tìm $m$ để phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm $x \in \left( {1;3} \right)$ .
-
A.
$- 13 < m < - 9$
-
B.
$3 < m < 9$
-
C.
$- 9 < m < 3$
-
D.
$- 13 < m < 3$
- Đặt ẩn phụ đưa phương trình về bậc hai.
- Tìm điều kiện để bài toán phụ có nghiệm thỏa mãn điều kiện của ẩn phụ,
Đặt $t = {2^x};x \in \left( {1;3} \right) \Rightarrow t = {2^x} \in \left( {2;8} \right)$
Xét hàm số \(y = {t^2} - 8t + 3\) trên \((2;8)\) có:
$y' = 2t - 8;$ $y' = 0 \Leftrightarrow 2t - 8 = 0 \Leftrightarrow t = 4\in (2;8)$
Bảng biến thiên:
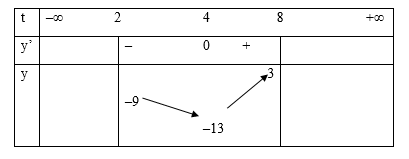
Căn cứ bảng biến thiên:
Phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm \(x \in \left( {1;3} \right) \Leftrightarrow - 13 < m < - 9\)
Đáp án : A

Các bài tập cùng chuyên đề

















