Đề bài

Một con bọ di chuyển từ điểm A đến điểm B dọc theo các đoạn thẳng mạng lưới lục giác như hình bên dưới.

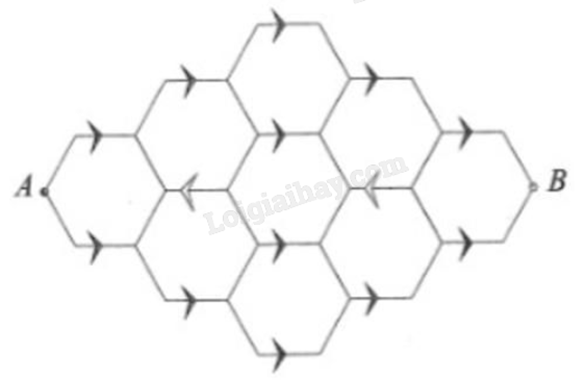
Các đoạn thẳng có dấu mũi tên chỉ được di chuyển theo hướng của mũi tên, các đoạn thẳng không có dấu mũi tên được di chuyển theo hướng tùy ý và con bọ không bao giờ di chuyển trên cùng một đoạn thẳng quá một lần. Vậy con bọ có bao nhiêu con đường khác nhau từ A đến B?

Phương pháp giải

Áp dụng công thức tính số tổ hợp.

Lời giải của GV Loigiaihay.com

Đáp án :

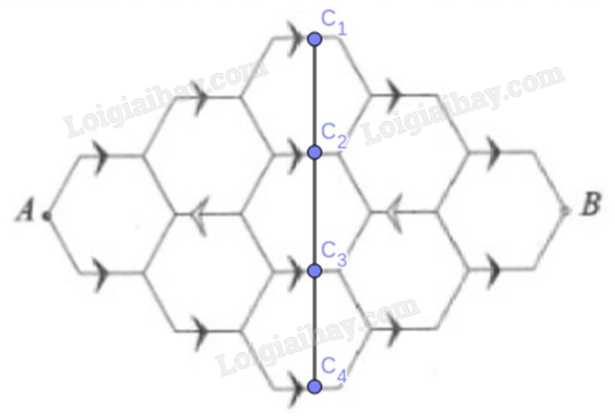
Có:

+ 5 con đường đi từ A đến \({C_1}\).

+ Có 5 con đường đi từ \({C_1}\) đến B.

Do đó, từ A đến B qua \({C_1}\) có 5.5 = 25 cách đi.

Tương tự với các điểm \({C_2},{C_3},{C_4}\), có tất cả \(4.25 = 100\) cách đi.

Nguồn: Hoidap247.

Mở rộng

Tổ hợp

Tổ hợp được sử dụng để chọn một tập hợp các phần tử từ một tập hợp lớn hơn mà không quan tâm đến thứ tự.

Số cách chọn k phần tử từ tập hợp n phần tử: \(C_n^k = \frac{{n!}}{{k!(n - k)!}}\).