Một bể bơi mini có dạng hình hộp chữ nhật với mặt đáy MNPQ là hình vuông. Hãy tìm độ dài cạnh MN của mặt đáy và chiều cao AM của bể bơi sao cho tổng diện tích các mặt làm bể bơi (bao gồm 4 mặt xung quanh và một mặt đáy) là nhỏ nhất, biết rằng thể tích của bể bơi là 4 \({m^3}\).
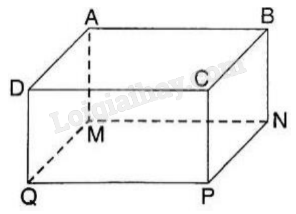
Gọi độ dài cạnh MN của mặt đáy và chiều cao AM của bể bơi lần lượt là x và y (mét; x > 0, y > 0).
Biểu diễn y theo x.
Biểu diễn diện tích các mặt của bể bơi theo x.
Áp dụng bất đẳng thức Cauchy cho ba số dương, tìm x để diện tích nhỏ nhất.
Gọi độ dài cạnh MN của mặt đáy và chiều cao AM của bể bơi lần lượt là x và y (mét; x > 0, y > 0).
Do thể tích bể bơi là 4 \({m^3}\) nên \({x^2}y = 4\) hay \(y = \frac{4}{{{x^2}}}\).
Tổng diện tích các mặt của bể bơi là:
\(S = 4xy + {x^2} = \frac{{16}}{x} + {x^2} = {x^2} + \frac{8}{x} + \frac{8}{x}\).
Áp dụng bất đẳng thức Cauchy cho ba số dương \(\frac{8}{x}\), \(\frac{8}{x}\) và \({x^2}\), ta được:
\(S = {x^2} + \frac{8}{x} + \frac{8}{x} \ge 3\sqrt[3]{{{x^2}.\frac{8}{x}.\frac{8}{x}}} = 3.4 = 12\).
Dấu “=” xảy ra khi và chỉ khi \({x^2} = \frac{8}{x}\), suy ra x = 2, y = 1.
Vậy để tổng diện tích các mặt làm bể bơi là nhỏ nhất thì MN = 2 (m), AM = 1 (m).

Các bài tập cùng chuyên đề

















