Formalin là dung dịch có chứa từ \(37 - 40\% \) Formaldehyde. Formaldehyde có khả năng kháng khuẩn, kháng nấm nên được dùng làm chất bảo quản trong y tế. Một nhà máy sản xuất Formalin đang có một lượng dung dịch Formaldehyde nồng độ \(15\% \) và một lượng Formaldehyde nồng độ \(65\% \).
a) Tính thể tích mỗi loại Formaldehyde trên để điều chế được \(300\) lít Formaldehyde \(35\% \). Giả sử nguyên liệu không bị hao hụt trong quá trình sản xuất.
b) Một cơ sở y tế đặt hàng nhà máy trên một đơn hàng Formalin. Nhà máy dùng \(200\) lít Formaldehyde \(15\% \) cùng một lượng Formaldehyde \(65\% \) để sản xuất ra Formalin. Hỏi thể tích của Formaldehyde \(65\% \) nằm trong khoảng nào thì có thể sản xuất được Formalin. (Kết quả làm tròn đến hàng đơn vị của lít)
a) Gọi \(x\,\left( {\rm{l}} \right),\,y\left( {\rm{l}} \right)\) lần lượt là thể tích của dung dịch Formaldehyde \(15\% \) và Formaldehyde \(65\% \) cần sử dụng (\(0 < x,y < 300\)).
Viết phương trình biểu diễn tổng thể tích hai loại dung dịch, nồng độ Formaldehyde trong dung dịch.
Từ đó ta lập được hệ phương trình.
Giải hệ phương trình vừa lập.
Kiểm tra lại điều kiện và kết luận.
b) Gọi \(x\,\left( {\rm{l}} \right)\) là thể tích Formaldehyde \(65\% \) (\(x > 0\)).
Biểu diễn tồng độ của Formaldehyde sau khi trộn hai loại dung dịch lại.
Do Formalin có nồng độ Formaldehyde từ \(37 - 40\% \) nên ta viết bất phương trình nồng độ dung dịch.
Giải các bất phương trình.
a) Gọi \(x\,\left( {\rm{l}} \right),\,y\left( {\rm{l}} \right)\) lần lượt là thể tích của dung dịch Formaldehyde \(15\% \) và Formaldehyde \(65\% \) cần sử dụng (\(0 < x,y < 300\)).
Vì tổng thể tích hai loại dung dịch là \(300\) nên ta có phương trình: \(x + y = 300\) (1).
Vì nồng độ Formaldehyde trong dung dịch lúc sau là \(35\% \) nên ta có: \(0,15x + 0,65y = 300.0,35\) hay \(0,15x + 0,65y = 105\) (2).
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 300\\0,15x + 0,65y = 105\end{array} \right.\)
Giải hệ phương trình, ta được \(\left\{ \begin{array}{l}x = 180\,\left( {TM} \right)\\y = 120\,\left( {TM} \right)\end{array} \right.\).
Vậy thể tích của Formaldehyde \(15\% \) và Formaldehyde \(65\% \) lần lượt là \(180\) lít và \(120\) lít.
b) Gọi \(x\,\left( {\rm{l}} \right)\) là thể tích Formaldehyde \(65\% \) (\(x > 0\)).
Nồng độ của Formaldehyde sau khi trộn hai loại dung dịch lại là \(\frac{{200.15\% + x.65\% }}{{200 + x}} = \frac{{0,65x + 30}}{{x + 200}}\).
Do Formalin có nồng độ Formaldehyde từ \(37 - 40\% \) nên ta có:
\(37\% \le \frac{{0,65x + 30}}{{x + 200}} \le 40\% \) hay \(0,37 \le \frac{{0,65x + 30}}{{x + 200}} \le 0,4\)
+) Giải bất phương trình: \(0,37 \le \frac{{0,65x + 30}}{{x + 200}}\)
\(\begin{array}{l}0,37 \le \frac{{0,65x + 30}}{{x + 200}}\\0,37\left( {x + 200} \right) \le 0,65x + 30\\0,37x + 74 - 0,65x - 30 \le 0\\ - 0,28x + 44 \le 0\\x \ge 157\end{array}\)
+) Giải bất phương trình: \(\frac{{0,65x + 30}}{{x + 200}} \le 0,4\)
\(\begin{array}{l}\frac{{0,65x + 30}}{{x + 200}} \le 0,4\\0,65x + 30 \le 0,4x + 80\\0,25x \le 50\\x \le 200\end{array}\)
Ta được \(x \ge 157\) và \(x \le 200\) hay \(157 \le x \le 200\).
Vậy thể tích Formaldehyde từ \(157\) lít đến \(200\) lít thì thu được Formalin.

Các bài tập cùng chuyên đề
Bài 1 :
Một hãng viễn thông nước ngoài có hai gói cước như sau:
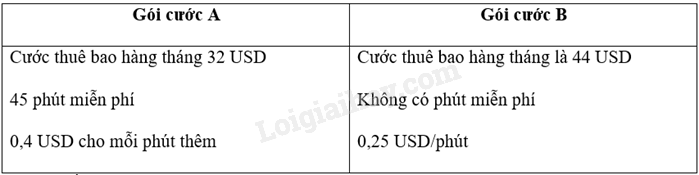
a) Hãy viết một phương trình xác định thời gian gọi (phút) mà phí phải trả trong cùng một tháng của hai gói cước là như nhau và giải phương trình đó.
b) Nếu khách hàng chỉ gọi tối đa là 180 phút trong 1 tháng thì nên dùng gói cước nào? Nếu khách hàng gọi 500 phút trong 1 tháng thì nên dùng gói cước nào?
Bài 2 :
Không sử dụng máy tính cầm tay, hãy đưa ra hai cách khác nhau để trả lời câu hỏi dưới đây: “Bất phương trình \(2x - 3 < 5x + 3\) nhận số nào trong các số sau làm nghiệm: \( - 3; - 2,55; - \frac{1}{7};\frac{2}{3};1,2\)?”. Trong hai cách đó, cách nào đòi hỏi ít tính toán hơn?
Bài 3 :
Chọn hãng xe nào?
Nhà máy dự định tổ chức một chuyến du lịch cho 35 công nhân được bình chọn là lao động xuất sắc. Anh Tùng được giao nhiệm vụ tìm hiểu chi phí thuê xe ô tô chở công nhân đi du lịch. Dưới đây là giá thuê xe do hai hàng xe đưa ra:
- Hãng A: Tiền thuê ban đầu là 2 triệu đồng, sau đó mỗi km của hành trình tính 8 nghìn đồng.
- Hãng B: Tiền thuê ban đầu là 1,5 triệu đồng, sau đó mỗi km của hành trình tính 9 nghìn đồng.
a) Lập bất phương trình diễn đạt giả định: “Tiền thuê xe của hãng A ít hơn tiền thuê xe của hãng B”.
b) Giải bất phương trình đó.
c) Nếu hành trình du lịch dự định của nhà máy dài 320km thì anh Tùng chọn hãng nào sẽ có lợi hơn về khoản phí thuê xe phải trả?
Bài 4 :
Số đo tính theo độ của ba góc A, B, C trong tứ giác ABCD lần lượt là x, 2x, 3(x - 10) với x > 10.
a) Viết một bất phương trình bậc nhất ẩn x.
b) Giải bất phương trình bậc nhất một ấn ở câu a.
c) Các góc có số đo là 2x và 3(x − 10) có bằng nhau được hay không? Vì sao?
Bài 5 :
Mức lương tối thiểu theo quy định ở Pháp năm 2022 là 10,25€ cho mỗi giờ làm việc.
Trong dịp hè, Laurent David làm thêm tại một khách sạn theo mức lương tối thiểu như quy định và anh ấy muốn kiếm được ít nhất 1500€ trong mùa hè này.
a) Hãy viết một bất phương trình mô tả tình huống này.
b) Hỏi anh ấy cần làm việc ít nhất bao nhiêu giờ để kiếm được số tiền trên? (€ là viết tắt của Euro, là loại tiền tệ mà 20 nước thuộc liên minh Châu Âu đang sử dụng chung)
Bài 6 :
Giải các phương trình và bất phương trình sau:
a) \(\left( {x - 1} \right)\left( {3x - 6} \right) = 0\)
b) \(\frac{2}{{x + 3}} - \frac{1}{{x - 2}} = \frac{{2x - 13}}{{\left( {x + 3} \right)\left( {x - 2} \right)}}\)
c) \(2x - 4 > 0\)
d) \(2 - 3x \le 4x + 5\)
Bài 7 :
1. Giải các phương trình và bất phương trình sau:
a) \({x^2} - 5x + 4\left( {x - 5} \right) = 0\)
b) \(\frac{x}{{x - 3}} = \frac{x}{{x + 3}} + \frac{{36}}{{{x^2} - 9}}\)
c) \(3x - 2 > 4\)
d) \(\frac{{3x - 1}}{4} + 5 \le \frac{{x - 1}}{2}\)
2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x + y = 8\\x - y = - 5\end{array} \right.\)
Bài 8 :
1. Giải các phương trình và bất phương trình sau:
a) \({x^2} + 2x - 3 = 0\)
b) \(\frac{{2x + 1}}{{2x}} - \frac{x}{{x + 2}} = 0\)
c) \(3x - 5 < 2x + 2\)
d) \(\frac{{2x + 3}}{2} \ge \frac{{1 - x}}{3} + 1\)
2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 4\\x + 2y = - 3\end{array} \right.\)
Bài 9 :
Cho hình vẽ, biết chu vi hình tam giác lớn hơn chu vi hình chữ nhật và \(x > 0\).
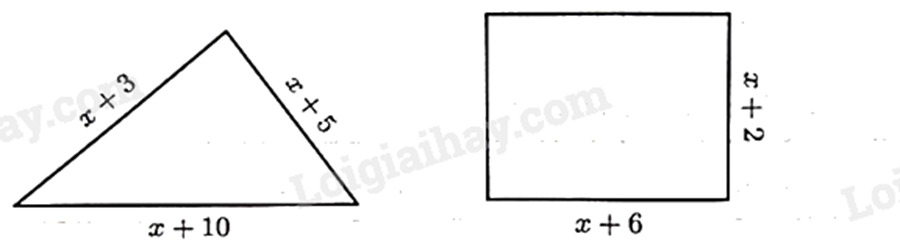
a) Chu vi hình tam giác và hình chữ nhật lần lượt là \(3x + 18\) và \(4x + 16\).
b) \(4x + 16 > 3x + 18\).
c) \(x < 2\)
d) Với x = 1 thì chu vi tam giác bằng diện tích hình chữ nhật.
Bài 10 :
Một ô tô dự định đi từ A đến B trong một thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 12,5km/h thì đến sớm hơn dự định 2 giờ, còn xe chạy chậm đi 10km/h thì đến nơi chậm mất 2,5 giờ.a) Tính vận tốc của xe lúc đầu, thời gian dự định và chiều dài quãng đường AB.
b) Trên quãng đường cao tốc CD = 150km có vận tốc giới hạn từ 50km/h đến 120km/h thì một ô tô đi hết cao tốc trong khoảng thời gian nào?
Bài 11 :
Một xí nghiệp dự tính chuyển hàng bằng hai xe tải và đang phân vân giữa việc mua hẳn hai chiếc xe tải hoặc thuê hai xe tải. Nếu mua hai xe với giá mỗi xe là 200 triệu đồng thì mỗi ngày xí nghiệp phải tốn 5 triệu đồng cho tất cả tài xế và nhiên liệu. Còn nếu thuê xe thì giá thuê một xe tải là 10 triệu đồng/ngày (đã bao gồm tiền công cho tài xế và nhiên liệu).a) Trong trường hợp xí nghiệp quyết định mua và xe tải mới mua cần phải bảo dưỡng định kì, xí nghiệp sẽ sử dụng kết hợp cả xe tải mua và xe tải thuê. Khi đó, tổng chi phí vận chuyển cho một đợt chuyển hàng 300 ngày là 4 tỉ đồng (bao gồm cả tiền mua xe). Hãy tính số ngày sử dụng xe tải mua và số ngày sử dụng xe tải thuê trong đợt chuyển hàng này.
b) Trong trường hợp xí nghiệp vẫn đang phân vân giữa việc mua xe và thuê xe thì sau bao nhiêu ngày phương án mua xe sẽ tiết kiệm hơn phương án thuê xe?
Bài 12 :
Nhân dịp khai trương, một nhóm gia đình muốn mua vé vào khu vui chơi. Biết rằng, khu vui chơi đã đưa ra hai chương trình khuyến mãi như sau:- Chương trình 1: mua vé người lớn với giá 100 000 đồng/1 vé thì sẽ được giảm 20 000 đồng cho mỗi vé trẻ em giá 50 0000 đồng/1 vé.
- Chương trình 2: mua vé người lớn với giá 80 000 đồng/1 vé thì giá vé trẻ em là 50 000 đồng/1 vé.
a) Nếu nhóm gia đình chọn mua theo chương trình 1 thì số tiền họ phải trả là 1 000 000 đồng, nếu nhóm gia đình chọn mua theo chương trình 2 thì số tiền họ phải trả là 1 060 000 đồng. Hỏi nhóm gia đình có bao nhiêu người.
b) Một nhóm gia đình khác gồm \(a\) người lớn và 4 trẻ em. Hỏi nhóm người này phải có tối thiểu là bao nhiêu người lớn để chọn chương trình 2 có lợi hơn chương trình 1?
Bài 13 :
Một bài thi trắc nghiệm gồm 20 câu hỏi, nếu trả lời đúng thì được 5 điểm, nếu trả lời sai thì bị trừ 2 điểm, nếu bỏ qua câu trả lời thì được 0 điểm.a) Bạn An tham dự bài thi và được 47 điểm. Biết An bỏ qua 5 câu. Hỏi An trả lời đúng mấy câu và trả lời sai mấy câu?
b) Bạn Hoa tham dự bài thi và được 59 điểm. Hỏi Hoa trả lời đúng mấy câu, trả lời sai mấy câu và bỏ qua bao nhiêu câu?
Bài 14 :
Một người đi taxi sẽ phải trả chi phí gồm: phí lúc mở cửa và cứ mỗi km di chuyển sẽ trả một số tiền cố định. Nhà ông bà ngoại của Nam cách nhà Nam 32 km. Biết rằng một chuyến đi 10km thì phải trả 109 000 đồng và một chuyến đi 6km thì phải trả 69 000 đồng.a) Nam muốn về thăm ông bà ngoại bằng cách đi xe taxi từ nhà. Hỏi Nam phải trả bao nhiêu tiền cho chuyến đi.
b) Để giảm chi phí, Nam tính toán cách di chuyển thứ hai đến nhà ông bà ngoại như sau: Nam đi taxi đến trạm xe buýt, rồi sau đó đi xe buýt theo tuyến đường đến nhà ông bà ngoại. Biết giá vé xe buýt là 50000 đồng. Hỏi trạm xe buýt cách nhà Nam bao xa thì với cách di chuyển thứ hai sẽ ít tốn chi phí hơn?


















Danh sách bình luận