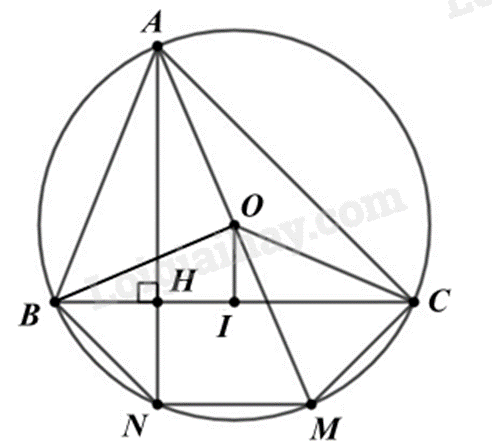
Cho tam giác ABC nhọn nội tiếp đường tròn tâm \(\left( O \right)\), đường cao AH, đường kính AM. Gọi I là trung điểm BC.
a) \(\widehat {ACM} = 45^\circ \).
b) \(\widehat {OAC} = \widehat {BAH}\).
c) \(OI{\mkern 1mu} {\rm{//}}{\mkern 1mu} AH\).
d) Gọi N là giao điểm của AH với đường tròn \(\left( O \right)\). Tứ giác BCMN là hình bình hành.
a) \(\widehat {ACM} = 45^\circ \).
b) \(\widehat {OAC} = \widehat {BAH}\).
c) \(OI{\mkern 1mu} {\rm{//}}{\mkern 1mu} AH\).
d) Gọi N là giao điểm của AH với đường tròn \(\left( O \right)\). Tứ giác BCMN là hình bình hành.
a) Sử dụng hai góc nội tiếp chắn nửa đường tròn bằng \(90^\circ \).
b) Sử dụng hai góc nội tiếp chắn cùng một cung thì bằng nhau để chứng minh \(\widehat {ABC} = \widehat {AMC}\).
Kết hợp với tổng hai góc phụ nhau để suy ra \(\widehat {OAC} = \widehat {BAH}\).
c) Chứng minh OI là đường cao nên \(OI \bot BC\), mà \(AH \bot BC\) nên \(AH//OI\).
d) Sử dụng hai góc nội tiếp chắn nửa đường tròn bằng \(90^\circ \).
Chứng minh MN // BC suy ra BCMN là hình thang. Chứng minh hai góc ở đáy \(\widehat {CBN} = \widehat {BCM}\) thông qua hai cung trên cùng một đường tròn gọi là bằng nhau nếu chúng có cùng số đo, suy ra BCMN là hình thang cân.
a) Sai
Vì \(\widehat {ACM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACM} = 90^\circ \).
b) Đúng
Xét (O) có: \(\widehat {ABC} = \widehat {AMC}\) (hai góc nội tiếp cùng chắn cung AC).
Mà \(\widehat {BAH} + \widehat {ABC} = 90^\circ \left( {AH \bot BC} \right)\)
Lại có: \(\widehat {OAC} + \widehat {AMC} = 90^\circ \) (tam giác ACM có \(\widehat {ACM} = 90^\circ \)).
Suy ra \(\widehat {BAH} + \widehat {ABC} = \widehat {OAC} + \widehat {AMC}\)
nên \(\widehat {BAH} = \widehat {OAC}\)
c) Đúng
Tam giác BOC cân tại O (OB = OC = R) có I là trung điểm của BC nên OI là đường trung tuyến đồng thời là đường cao.
Suy ra \(OI \bot BC\)
Mà \(AH \bot BC\) nên \(OI//AH\).
d) Sai
Xét (O) có \(\widehat {ANM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ANM} = 90^\circ \) suy ra \(AN \bot NM\)
Mà \(BC \bot AN\) suy ra \(MN//BC\). Do đó tứ giác BCMN là hình thang. (1)
Ta lại có: \(\widehat {BAN} = \widehat {CAM}\) (vì \(\widehat {BAH} = \widehat {OAC}\))
Do đó: $\overset\frown{BN}=\overset\frown{CM}$
$\overset\frown{BN}+\overset\frown{MN}=\overset\frown{CM}+\overset\frown{MN}$
$\overset\frown{BNM}=\overset\frown{CMN}$
Do đó \(\widehat {BCM} = \widehat {CBN}\) (2)
Từ (1) và (2) suy ra tứ giác BCMN là hình thang cân.
Đáp án: SĐĐS

Các bài tập cùng chuyên đề
Bài 1 :
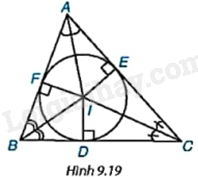
Cho tam giác ABC có ba đường phân giác đồng quy tại điểm I. Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB (H.9.19).
a) Hãy giải thích vì sao các điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi (I) là đường tròn trên. Hãy giải thích vì sao (I) tiếp xúc với các cạnh của tam giác ABC.
Bài 2 :
Mỗi tam giác có bao nhiêu đường tròn nội tiếp? Có bao nhiêu tam giác cùng ngoại tiếp một đường tròn?
Bài 3 :
Theo gợi ý trong Hình 10, nêu cách xác định hai điểm I và O của tình huống trong khởi động (trang 65).
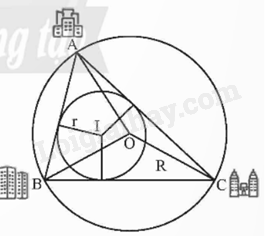
Ba cụm dân cư A, B, C nối với nhau bởi ba con đường AB, BC, CA như trong hình dưới đây. Người ta muốn tìm địa điểm O để xây một trường học và địa điểm I để lập một trạm cứu hộ xe, sao cho O cách đều ba điểm A, B, C và I cách đều ba con đường. Làm thế nào để xác định hai điểm O và I?
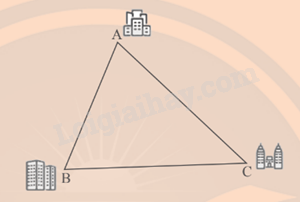
Bài 4 :
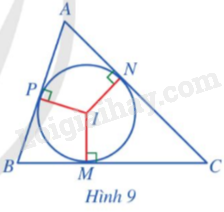
Cho tam giác ABC và đường tròn (I) (Hình 9). Nêu vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I).
Bài 5 :
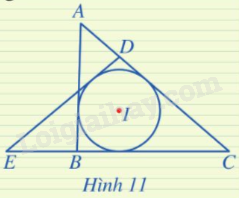
Trong Hình 11, đường tròn (I) là đường tròn nội tiếp những tam giác nào?
Bài 6 :
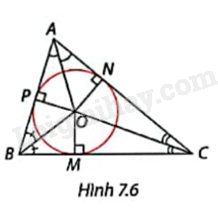
Trong Hình 7.6, O là giao điểm của ba đường phân giác của \(\Delta \)ABC và OM, ON, OP là các đường vuông góc hạ từ O xuống ba cạnh của tam giác. Giải thích vì sao đường tròn tâm O bán kính OM tiếp xúc cả ba cạnh của \(\Delta \)ABC.
Bài 7 :
Cho đường tròn \(\left( I \right)\) nội tiếp tam giác \(ABC\) với các tiếp điểm trên cạnh \(AB,\,AC,\,BC\) lần lượt là \(E,\,F,\,D\). Biết \(\widehat A = 40^\circ ;\,\,\widehat B = 60^\circ \).
a) Điểm \(I\) là trọng tâm của \(\Delta ABC\).
b) \(\widehat {EIF} + \widehat {BAC} = 180^\circ \).
c) Số đo góc \(\widehat {BIC}\) bằng \(110^\circ \).
d) \(2AE = AB + AC - BC\).
Bài 8 :
Cho đường tròn (I; r) cố định. Một tam giác ABC thay đổi, có chu vi bằng 16 cm và luôn ngoại tiếp đường tròn (I; r). Một tiếp tuyến song song với BC cắt các cạnh AB, AC lần lượt tại M và N. Tìm dộ dài BC để MN có độ dài lớn nhất.
Bài 9 :
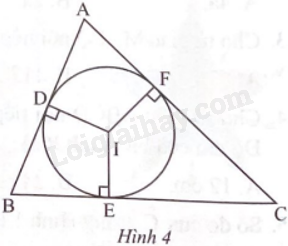
Cho tam giác ABC ngoại tiếp đường tròn (I; r); D, E, F lần lượt là các tiếp điểm của cạnh AB, BC, AC với đường tròn (I; r) (Hình 4).
a) Ba đường trung trực của tam giác ABC cắt nhau tại I.
b) AD = AF.
c) BD + CF = BC
d) IE = r
Bài 10 :
Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng \(\widehat {EIF} + \widehat {BAC} = {180^o}\).
Bài 11 :
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Ba đường cao AD, BE và CF của tam giác ABC cắt nhau tại H. Gọi AK là đường kính của (O). Chứng minh rằng:
a) \(BH = CK,CH = BK\);
b) \(AD.AK = AB.AC\).
Bài 12 :
Một đường tròn là đường tròn nội tiếp nếu nó:
-
A.
Đi qua các đỉnh của một tam giác.
-
B.
Tiếp xúc với các đường thẳng chứa các cạnh của tam giác.
-
C.
Tiếp xúc với các cạnh của tam giác.
-
D.
Nằm trong một tam giác.


















Danh sách bình luận