Đề bài

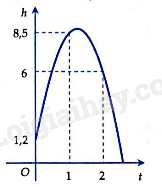
Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ \(Oth,\) trong đó \(t\) là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; \(h\) là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao \(1,2m\). Sau đó \(1\) giây, nó đạt độ cao \(8,5m\)và \(2\) giây sau khi đá lên, nó đạt độ cao \(6m\). Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên (tính chính xác đến hàng phần trăm)?

Phương pháp giải

Lập phương trình của parabol quỹ đạo theo thời gian t.

Lời giải của GV Loigiaihay.com

Gọi phương trình của parabol quỹ đạo là \(h = a{t^2} + bt + c\).

Từ giả thiết suy ra parabol đi qua các điểm \(\left( {0;1;2} \right)\), \(\left( {1;8;5} \right)\) và \(\left( {2;6} \right)\).

 

Từ đó ta có:

\(\left\{ \begin{array}{l}c = 1,2\\a + b + c = 8,5\\4a + 2b + c = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 4,9\\b = 12,2\\c = 1,2\end{array} \right.\).

Vậy phương trình của parabol quỹ đạo là \(h =  - 4,9{t^2} + 12,2t + 1,2\).

Giải phương trình:

\(h = 0 \Leftrightarrow  - 4,9{t^2} + 12,2t + 1,2 = 0\) ta tìm được một nghiệm dương là \(t \approx 2,58\).