Đề bài

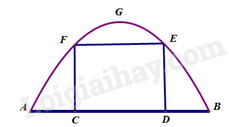
Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B.

Phương pháp giải

Tìm công thức hàm số của parabol (P) bằng cách chọn hệ trục tọa độ phù hợp, thay tọa độ các điểm đồ thị đi qua vào công thức tổng quát.

Tìm tọa độ A, B bằng cách giải phương trình hoành độ giao điểm của hàm số với trục hoành. Tính khoảng cách AB.

Lời giải của GV Loigiaihay.com

 

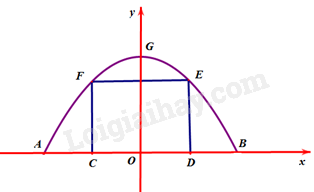
Gắn hệ trục tọa độ Oxy  như hình vẽ, chiếc cổng là 1 phần của parabol \(\left( P \right):y = a{x^2} + bx + c\) với \(a < 0\).

Do parabol \((P)\) đối xứng qua trục tung nên có trục đối xứng \(x = 0 \Rightarrow  - \frac{b}{{2a}} = 0 \Leftrightarrow b = 0\) .

Chiều cao của cổng parabol là 4m nên \(G\left( {0;4} \right) \Rightarrow c = 4\)

\( \Rightarrow \left( P \right):y = a{x^2} + 4\).

Lại có, kích thước cửa ở giữa là 3m x 4m nên \(E\left( {2;3} \right) \Rightarrow 3 = 4a + 4 \Rightarrow a =  - \frac{1}{4}\) .

Vậy \(\left( P \right):y =  - \frac{1}{4}{x^2} + 4\).

Ta có \( - \frac{1}{4}{x^2} + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x =  - 4\end{array} \right.\)  nên \(A\left( { - 4;0} \right);B\left( {4;0} \right)\) hay \(AB = 8\).