Cho tam giác ABC có góc A bằng \({120^o}\). Các đường trung trực của AB và Ac lần lượt cắt Bc tại M và N. Tính số đo góc MAN.
Sử dụng tính chất của tam giác cân
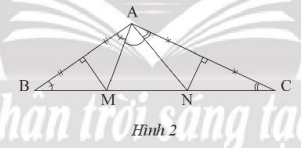
Ta có MA = MB suy ra tam giác MAB cân tại M suy ra \(\widehat {MAB} = \widehat {MBA} = \widehat B\)
Tương tự, ta có tam giác NAC cân tại N suy ra \(\widehat {NAC} = \widehat {NCA} = \widehat C\)
Ta có: \(\widehat {MAN} = \widehat {BAC} - \left( {\widehat {MAB} + \widehat {NAC}} \right) = {120^o} - \left( {\widehat B + \widehat C} \right) = {120^o} - {60^o} = {60^o}\)

Các bài tập cùng chuyên đề
Bài 1 :
Mỗi tam giác có mấy đường trung trực
Bài 2 :
Cho tam giác ABC, em hãy dùng thước kẻ và compa vẽ đường trung trực xy của cạnh BC.
Bài 3 :
Ở Hình 1, cho biết AE = AF và \(\widehat {ABC} = \widehat {ACB}\). Chứng minh AH là đường trung trực của BC.
Bài 4 :
Hình 121 minh họa biển giới thiệu quần thể di tích, danh thắng cấp Quốc gia núi Dũng Quyết và khu vực Phượng Hoàng Trung Đô ở tỉnh Nghệ An (Hình 120).

Làm thế nào để xác định được vị trí cách đều ba địa điểm được minh họa trong Hình 121?
Bài 5 :
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung trực của tam giác ABC.
Bài 6 :
Cho C là trung điểm của đoạn thẳng AB. Gọi Ax, By là hai đường thẳng vuông góc với AB tại A và tại B. Một đường thẳng qua C cắt Ax tại M, cắt By tại P. Điểm N nằm trên tia đối của tia BP sao cho góc MCN là góc vuông. Gọi H là hình chiếu của C trên MN.
Chứng minh:
a) AM + BN = MN;
b) CM là đường trung trực của AH, CN là đường trung trực của BH;
c) Góc AHB là góc vuông.
Bài 7 :
Cho tam giác ABC có đường trung trực cạnh AC đi qua đỉnh B, chứng minh tam giác ABC là tam giác cân
Bài 8 :
Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Chứng minh AH là đường trung trực của BC.


















Danh sách bình luận