Cho tam giác ABC, biết \(A\left( {1;4} \right),B\left( {0;1} \right),C\left( {4;3} \right)\).
a) Lập phương trình tổng quát của đường thẳng BC.
b) Lập phương trình tham số của đường trung tuyến AM.
c) Lập phương trình tổng quát của đường cao AH.
Phương trình tổng quát đường thẳng đi qua \(M\left( {{x_1},{y_1}} \right)\) nhận \(\overrightarrow {{a_1}} = \left( {a;b} \right)\) là vectơ pháp tuyến là: \(a\left( {x - {x_1}} \right) + b\left( {y - {y_1}} \right) = 0\).
Ta có \(A\left( {1;4} \right),B\left( {0;1} \right),C\left( {4;3} \right)\).
a) \(\overrightarrow {BC} = \left( {4;2} \right) \Rightarrow \overrightarrow n = \left( {1; - 2} \right) \Rightarrow BC:1\left( {x - 0} \right) - 2\left( {y - 1} \right) = 0 \Rightarrow x - 2y + 2 = 0\).
b) M là trung điểm của BC → \(\begin{array}{l}M\left( {2;2} \right) \Rightarrow \overrightarrow {AM} = \left( {1; - 2} \right)\\ \Rightarrow AM:\left\{ \begin{array}{l}x = 1 + t\\y = 4 - 2t\end{array} \right.\end{array}\).
c) \(\overrightarrow {AH} \bot \overrightarrow {BC} \Rightarrow \overrightarrow {{n_{AH}}} = \overrightarrow {BC} = \left( {2;1} \right)\)
\( \Rightarrow AH:2\left( {x - 1} \right) + 1\left( {y - 4} \right) = 0 \Rightarrow AH:2x + y - 6 = 0\).

Các bài tập cùng chuyên đề
Bài 1 :
Phương trình đường thẳng đi qua hai điểm A(-2; 4), B(-6; 1) là:
-
A.
\(3x + 4y - 10 = 0.\)
-
B.
\(3x - 4y + 22 = 0.\)
-
C.
\(3x - 4y + 8 = 0.\)
-
D.
\(3x - 4y - 22 = 0\)
Bài 2 :
Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm A(0;-1), B(3;0). Phương trình đường thẳng AB là
-
A.
\(x - 3y + 1 = 0\)
-
B.
\(x + 3y + 3 = 0\)
-
C.
\(x - 3y - 3 = 0\)
-
D.
\(3x + y + 1 = 0\)
Bài 3 :
Trong mặt phẳng \(Oxy\) cho hai điểm\(A\left( {1; - 3} \right)\), \(B\left( { - 2;5} \right)\). Viết phương trình tổng quát của đường thẳng đi qua hai điểm $A,{\rm{ }}B$.
-
A.
\(8x + 3y + 1 = 0\).
-
B.
\(8x + 3y - 1 = 0\).
-
C.
\( - 3x + 8y - 30 = 0\).
-
D.
\( - 3x + 8y + 30 = 0\).
Bài 4 :
Đường thẳng đi qua hai điểm A(-1;4) và B(2;-7) có phương trình là:
-
A.
3x + 11y – 1 = 0
-
B.
11x + 3y + 1 = 0
-
C.
11x + 3y – 1 = 0
-
D.
3x + 11y + 1 = 0
Bài 5 :
Lập phương trình tham số và phương trình tổng quát của đường thẳng đi qua 2 điểm phân biệt \(A\left( {{x_1};{y_1}} \right);B\left( {{x_2};{y_2}} \right)\) cho trước.
Bài 6 :
Trong mặt phẳng toạ độ, cho\(\vec n = \left( {2;{\rm{ }}1} \right),{\rm{ }}\vec v{\rm{ }} = {\rm{ }}\left( {3,{\rm{ }}2} \right),{\rm{ }}A\left( {1,{\rm{ }}3} \right),{\rm{ }}B\left( { - 2;{\rm{ }}1} \right)\) .
a) Lập phương trình tổng quát của đường thẳng \({\Delta _1}\) đi qua A và có vectơ pháp tuyến \(\overrightarrow n \).
b) Lập phương trình tham số của đường thẳng \({\Delta _2}\), đi qua B và có vectơ chỉ phương \(\overrightarrow v \).
c) Lập phương trình tham số của đường thẳng AB.
Bài 7 :
Cho phương trình hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = - 1 - 2t\\y = 2 - 5t\end{array} \right.\) và \({\Delta _2}:2x + 3y - 5 = 0\).
a) Lập phương trình tổng quát của \({\Delta _1}\).
b) Lập phương trình tham số của \({\Delta _2}\).
Bài 8 :
Trong mặt phẳng toạ độ, cho tam giác ABC có A(1; 2), B(3; 0) và C(-2; -1).
a) Lập phương trình đường cao kẻ từ A.
b) Lập phương trình đường trung tuyến kẻ từ B.
Bài 9 :
Viết phương trình tham số và phương trình tổng quát của đường thẳng \(\Delta \) trong các trường hợp sau:
a) Đường thẳng \(\Delta \) đi qua điểm \(A(1;1)\)và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\)
Bài 10 :
Viết phương trình đường thẳng \({d_1}\):
a) Đi qua điểm \(A(2;3)\) và song song với đường thẳng \({d_2}:x + 3y + 2 = 0\)
b) Đi qua điểm \(B(4; - 1)\) và vuông góc với đường thẳng \({d_3}:3x - y + 1 = 0\)
Bài 11 :
Lập phương trình tham số và phương trình tổng quát của đường thẳng d trong mỗi trường hợp sau:
a) d đi qua điểm \(A( - 1;5)\) và có vectơ chỉ phương \(\overrightarrow u = (2;1)\)
b) d đi qua điểm \(B(4; - 2)\) và có vectơ pháp tuyến là \(\overrightarrow n = (3; - 2)\)
c) d đi qua \(P(1;1)\) và có hệ số góc \(k = - 2\)
d) d đi qua hai điểm \(Q(3;0)\)và \(R(0;2)\)
Bài 12 :
Cho tam giác ABC biết \(A(2;5),B(1;2)\) và \(C(5;4)\).
a) Lập phương trình tổng quát của đường thẳng BC.
b) Lập phương trình tham số của đường trung tuyến AM.
c) Lập phương trình của đường cao AH.
Bài 13 :
Lập phương trình tham số và phương trình tổng quát của đường thẳng \(\Delta \) trong mỗi trường hợp sau:
a) \(\Delta \) đi qua \(A(2;1)\) và song song với đường thẳng \(3x + y + 9 = 0\).
b) \(\Delta \)đi qua \(B( - 1;4)\) và vuông góc với đường thẳng \(2x - y - 2 = 0\).
Bài 14 :
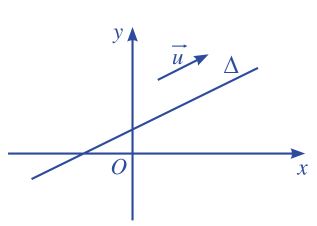
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \) . Vẽ vectơ \(\overrightarrow u \) (\(\overrightarrow u \ne \overrightarrow 0 \)) có giá song song (hoặc trùng) với đường thẳng \(\Delta \).
Bài 15 :
Một máy bay cất cánh từ sân bay theo một đường thẳng nghiêng với phương nằm ngang một góc 20°, vận tốc cất cánh là 200 km/h. Hình 24 minh hoạ hình ảnh đường bay của máy bay trên màn hình ra đa của bộ phận không lưu. Để xác định vị trí của máy bay tại những thời điểm quan trọng (chẳng hạn: 30 s, 60 s, 90 s, 120 s), người ta phải lập phương trình đường thẳng mô tả đường bay.
Làm thế nào để lập phương trình đường thẳng trong mặt phẳng tọa độ?
Bài 16 :
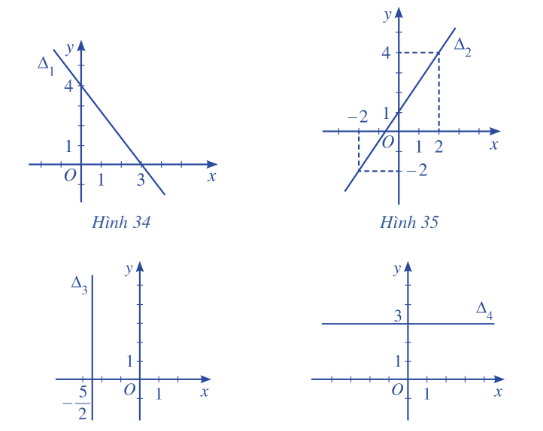
Lập phương trình đường thẳng trong các Hình 34, 35, 36, 37:
Bài 17 :
Cho ba điểm A(2;4), B(-1; 2) và C(3;-1). Viết phương trình đường thẳng đi qua B đồng thời cách đều A và C.
Bài 18 :
Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường hợp sau:
a) d đi qua điểm \(A\left( { - 3;2} \right)\) và có một vectơ pháp tuyến là \(\overrightarrow n = \left( {2; - 3} \right)\).
b) d đi qua điểm \(B\left( { - 2; - 5} \right)\) và có một vectơ chỉ phương là \(\overrightarrow u = \left( { - 7;6} \right)\).
c) d đi qua hai điểm \(C\left( {4;3} \right),D\left( {5;2} \right)\).
Bài 19 :
Trong mặt phẳng \(Oxy\), cho điểm \(D\left( {0;2} \right)\) và hai vector \(\overrightarrow n = \left( {1; - 3} \right),\overrightarrow u = \left( {1;3} \right)\)
a) Viết phương trình tổng quát của đường thẳng d đi qua D và nhận \(\overrightarrow n \) là một vector pháp tuyến.
b) Viết phương trình tổng quát của đường thẳng \(\Delta \) đi qua D và nhận \(\overrightarrow u \) là một vector chỉ phương.
Bài 20 :
Trong mặt phẳng \(Oxy\), cho ba điểm \(A\left( {1;2} \right);B\left( {0; - 1} \right)\) và \(C\left( { - 2;3} \right)\). Lập phương trình tổng quát của đường thẳng đi qua A và vuông góc với đường thẳng BC.
Bài 21 :
Trong mặt phẳng \(Oxy\), cho hai điểm \(A\left( {1;2} \right)\) và \(B\left( {2;3} \right)\). Tìm một vector chỉ phương của đường thẳng AB và viết phương trình tham số của đường thẳng AB.
Bài 22 :
Trong mặt phẳng \(Oxy\), cho đường thẳng d có phương trình \(y = - 2x + 3\). Viết phương trình tham số và phương trình tổng quát của đường thẳng d.
Bài 23 :
Trong mặt phẳng \(Oxy\), cho tam giác ABC có tọa độ ba đỉnh \(A\left( {0; - 1} \right);B\left( {2;3} \right)\) và \(C\left( { - 4;1} \right)\). Lập phương trình tham số của đường trung bình ứng với cạnh BC của tam giác ABC.
Bài 24 :
Trong mặt phẳng \(Oxy\), cho đường thẳng \(\Delta :2x + y - 5 = 0\).
a) Viết phương trình đường thẳng d đi qua điểm \(A\left( {3;1} \right)\) và song song với đường thẳng \(\Delta \).
b) Viết phương trình đường thẳng k đi qua điểm \(B\left( { - 1;0} \right)\) và vuông góc với đường thẳng \(\Delta \).
c) Lập phương trình đường thẳng a song song với đường thẳng \(\Delta \) và cách điểm O một khoảng bằng \(\sqrt 5 \).
Bài 25 :
Cho hai điểm \(A\left( { - 1;0} \right)\) và \(B\left( { - 2;3} \right)\). Phương trình đường thẳng đi qua B và vuông góc với AB là:
A. \(x - 3y + 11 = 0\)
B. \(x - 3y + 1 = 0\)
C. \( - x - 3y + 7 = 0\)
D. \(3x + y + 3 = 0\)
Bài 26 :
Đường thẳng đi qua \(A\left( {1; - 1} \right)\) và \(B\left( { - 2; - 4} \right)\) có phương trình là:
A. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 1 - 3t\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = - 2 + t\\y = - 4 - t\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 1 - 2t\\y = - 1 - 4t\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = - 2 + t\\y = - 4 + t\end{array} \right.\)
Bài 27 :
Trong mặt phẳng \(Oxy\), cho điểm \(M\left( { - 3;2} \right)\) và vector \(\overrightarrow u = \left( {2; - 5} \right)\). Viết phương trình tham số của đường thẳng d đi qua M và nhận \(\overrightarrow u \) là một vector chỉ phương.
Bài 28 :
Trong mặt phẳng \(Oxy\), cho điểm \(N\left( {2; - 1} \right)\) và vector \(\overrightarrow n = \left( {3; - 1} \right)\). Viết phương trình tham số của đường thẳng d đi qua N và nhận \(\overrightarrow n \) là một vector pháp tuyến.
Bài 29 :
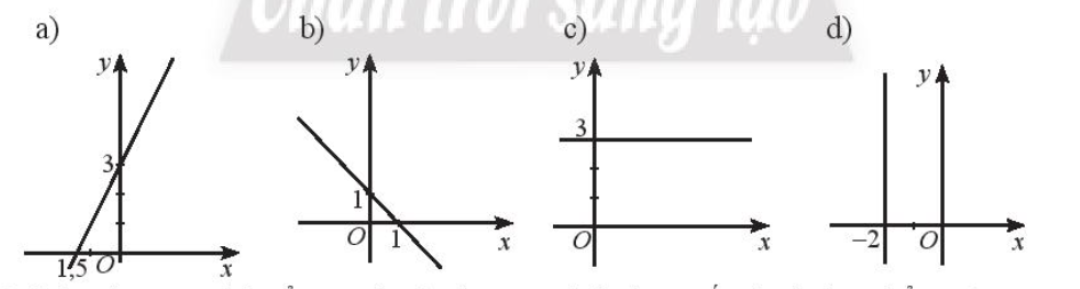
Tìm các giá trị của tham số a, b, c để phương trình \(ax + by + c = 0\) có thể biểu diễn được các đường thẳng trong hình dưới đây.
Bài 30 :
Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường hợp sau:
a) d đi qua điểm \(M\left( {2;2} \right)\) và vectơ chỉ phương \(\overrightarrow u = \left( {4;7} \right)\).
b) d đi qua điểm \(N\left( {0;1} \right)\) và có vectơ pháp tuyến là \(\overrightarrow n = \left( { - 5;3} \right)\).
c) d đi qua \(A\left( { - 2; - 3} \right)\) và có hệ số góc \(k = 3\).
d) d đi qua hai điểm \(P\left( {1;1} \right),Q\left( {3;4} \right)\).


















Danh sách bình luận