Một công nhân theo kế hoạch cần phải làm 120 sản phẩm trong một số giờ dự kiến, với số sản phẩm dự kiến làm trong một giờ là \(x\) sản phẩm. Sau khi làm được 2 giờ với năng suất dự kiến, công nhân đó đã tăng năng suất được 3 sản phẩm mỗi giờ, vì vậy công nhân đó đã hoàn thành kế hoạch sớm hơn thời gian dự kiến.
a) Hãy viết biểu thức biểu thị thời gian công nhân đó dự kiến hoàn thành kế hoạch.
b) Hãy viết biểu thức biểu thị thời gian công nhân đó hoàn thành kế hoạch sớm hơn thời gian dự kiến.
a) Áp dụng công thức tính thời gian hoàn thành = tổng số sản phẩm làm được : số sản phẩm làm được trong 1 giờ.
b) Áp dụng công thức tính thời gian hoàn thành = tổng số sản phẩm làm được : số sản phẩm làm được trong 1 giờ.
Thời gian hoàn thành sớm hơn dự kiến = thời gian dự kiến – thời gian hoàn thành thực tế.
a) Biểu thức biểu thị thời gian dự kiến người công nhân đó hoàn thành kế hoạch là: \(\frac{{120}}{x}\) (giờ)
b) Trong 2 giờ công nhân sản xuất với năng suất dự kiến, người công nhân làm được: \(2x\) (sản phẩm).
Khi đó số sản phẩm còn lại là \(120 - 2x\) (sản phẩm)
Sau khi tăng năng suất thì mỗi giờ công nhân sản xuất được: \(x + 3\) sản phẩm.
Người đó sản xuất \(120 - 2x\) trong thời gian là: \(\frac{{120 - 2x}}{{x + 3}}\) (giờ)
Biểu thức biểu thị thời gian thực tế công nhân đó hoàn thành số sản phẩm là: \(2 + \frac{{120 - 2x}}{{x + 3}}\) (giờ)
Vậy biểu thức biểu thị thời gian công nhân đó hoàn thành kế hoạch sớm hơn thời gian dự kiến là:
\(\begin{array}{l}\frac{{120}}{x} - \left( {2 + \frac{{120 - 2x}}{{x + 3}}} \right)\\ = \frac{{120}}{x} - 2 - \frac{{120 - 2x}}{{x + 3}}\\ = \frac{{120\left( {x + 3} \right) - 2x\left( {x + 3} \right) - x\left( {120 - 2x} \right)}}{{x\left( {x + 3} \right)}}\\ = \frac{{120x + 360 - 2{x^2} - 6x - 120x + 2{x^2}}}{{x\left( {x + 3} \right)}}\\ = \frac{{360 - 6x}}{{x\left( {x + 3} \right)}}\end{array}\)

Các bài tập cùng chuyên đề
Bài 1 :
Biểu thức nào dưới đây là phân thức đại số?
-
A.
\(\frac{{x + y}}{{\sqrt {7z} }}\)
-
B.
\(\frac{{{x^3} - 3{x^2} + 2}}{{xz - y}}\)
-
C.
\(\frac{{5{x^2}}}{{\frac{1}{z}}}\)
-
D.
\(\frac{{{x^2} + 2\sqrt x - 9}}{{0.yz}}\)
Bài 2 :

Bài 3 :
a) Viết biểu thức biểu thị các đại lượng sau đây:
- Chiều rộng của hình chữ nhật có chiều dài bằng \(a\) (m) và diện tích bằng \(3\)\({m^2}\) .
- Thời gian để một người thợ làm được \(x\) sản phẩm, biết rằng mỗi giờ người đó làm được \(y\) sản phẩm.
- Năng suất trung bình của một mảnh ruộng gồm hai thửa, một thửa có diện tích \(a\) (ha) cho thu hoạch được \(m\) tấn lúa, thửa kia có diện tích \(b\) (ha) cho thu hoạch \(n\) tấn lúa.
b) Các biểu thức trên có đặc điểm bào giống nhau? Chúng có phải là đa thức không?
Bài 4 :
Trong các biểu thức sau, biểu thức nào là các phân thức?
\(\dfrac{{3x + 1}}{{2x - 1}}\) ; \(2{x^2} - 5x + 3\) ; \(\dfrac{{x + \sqrt x }}{{3x + 2}}\)
Bài 5 :
Biểu thức nào sau đây không phải là phân thức?
A. \({x^2}y + y\)
B. \(\dfrac{{3xy}}{{\sqrt 2 z}}\)
C. \(\dfrac{{\sqrt x }}{2}\)
D. \(\dfrac{{a + b}}{{a - b}}\)
Bài 6 :
Trong các biểu thức sau, biểu thức nào là phân thức?
\(a)\dfrac{{{x^2}y + x{y^2}}}{{x - y}}\)
\(b)\dfrac{{{x^2} - 2}}{{\dfrac{1}{x}}}\)
Bài 7 :
Cho hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\). Nêu quy tắc để hai phân số đó bằng nhau.
Bài 8 :
Mỗi cặp phân thức sau có bằng nhau không? Vì sao?
a) \(\dfrac{{x + y}}{{{x^2} - {y^2}}}\) và \(\dfrac{1}{{x - y}}\)
b) \(\dfrac{x}{{{x^2} - 1}}\) và \(\dfrac{1}{{x - 1}}\)
Bài 9 :
Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
a) \(\dfrac{{3x}}{2} = \dfrac{{15xy}}{{10y}}\)
b) \(\dfrac{{3x - 3y}}{{2y - 2x}} = \dfrac{{ - 3}}{2}\)
c) \(\dfrac{{{x^2} - x + 1}}{x} = \dfrac{{{x^3} + 1}}{{x\left( {x + 1} \right)}}\)
Bài 10 :
Ta đã biết kết quả của phép chia số nguyên a cho số nguyên b khác 0 được gọi là phân số \(\dfrac{a}{b}\). . Kết quả của phép chia đa thức P cho đa thức Q khác đa thức 0 cũng có thể được viết dưới dạng \(\dfrac{P}{Q}\). Khi đó, biểu thức \(\dfrac{P}{Q}\) được gọi là gì?
Bài 11 :
a) Tính tỉ số chu vi của hình chữ nhật được tô vàng và hình chữ nhật được tô xanh trong Hình 2.1 theo \(x.\)
b) Tính tỉ số diện tích của hình chữ nhật được tô vàng và hình chữ nhật được tô xanh trong hình 2.1 theo \(x.\)
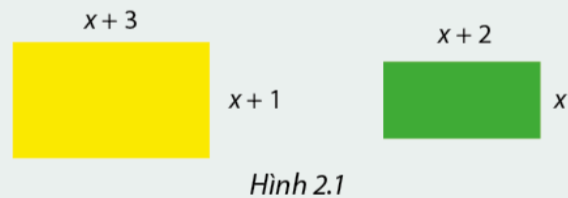
Bài 12 :
Viết một phân thức có tử thức và mẫu thức là các đa thức bậc ba của hai biến.
Bài 13 :
Viết một phân thức có tử thức và mẫu thức là các đa thức bậc ba có bốn hạng tử.
Bài 14 :
Viết một phân thức có tử thức và mẫu thức là các đa thức bậc bốn của cùng hai biến và có ba hạng tử.
Bài 15 :
Trong một cuộc đua xe đạp, các vận động viên phải hoàn thành ba chặng đua bao gồm 9 km leo dốc; 5 km xuống dốc và 36 km đường bằng phẳng. Vận tốc của một vận động viên trên chặng đường bằng phẳng hơn vận tốc leo dốc 5 km/h và kém vận tốc xuống dốc 10 km/h. Nếu biết vận tốc của vận động viên trên chặng đường bằng phẳng thì có tính được thời gian hoàn thành cuộc đua của vận động viên đó không?
Bài 16 :
Trong tình huống mở đầu, giả sử vận tốc trung bình của một vận động viên đi xe đạp trên 36 km đường bằng phẳng là x (km/h). Hãy viết biểu thức biểu thị thời gian vận động viên đó hoàn thành chặng leo dốc, chặng xuống dốc, chặng đường bằng phẳng
Bài 17 :
Viết biểu thức biểu thị tỉ số giữa chiều rộng và chiều dài của một hình chữ nhật có chiều rộng là x (cm) và chiều dài là y (cm)
Bài 18 :
Trong các cặp phân thức sau, cặp phân thức nào có cùng mẫu thức?
a) \(\frac{{ - 20{\rm{x}}}}{{3{y^2}}}\) và \(\frac{{4{{\rm{x}}^3}}}{{5{y^2}}}\)
b) \(\frac{{5{\rm{x}} - 10}}{{{x^2} + 1}}\)và \(\frac{{5{\rm{x}} - 10}}{{{x^2} - 1}}\)
c) \(\frac{{5{\rm{x}} + 10}}{{4{\rm{x}} - 8}}\)và \(\frac{{4 - 2{\rm{x}}}}{{4\left( {x - 2} \right)}}\)
Bài 19 :
Tròn: \(\frac{{3 - 2{\rm{x}}}}{{3 + \frac{1}{x}}}\) không phải là phân thức.
Vuông: \(\frac{{3 - 2{\rm{x}}}}{{3 + \frac{1}{x}}}\) là phân thức chứ.
Theo em, bạn nào đúng?
Bài 20 :
Viết tử thức và mẫu thức của phân thức \(\frac{{5{\rm{x}} - 2}}{3}\)
Bài 21 :
Trong các cặp phân thức sau, cặp phân thức nào có mẫu giống nhau?
\(a)\frac{{ - 20{\rm{x}}}}{{3{y^2}}}\) và \(\frac{{4y}}{{5{y^2}}}\)
\(b)\frac{{3{\rm{x}} - 1}}{{{x^2} + 1}}\) và \(\frac{{3{\rm{x}} - 1}}{{x + 1}}\)
\(c)\frac{{x - 1}}{{3{\rm{x}} + 6}}\) và \(\frac{{x + 1}}{{3\left( {x + 2} \right)}}\)
Bài 22 :
Một ô tô chạy với vận tốc là x (km/h)
a) Viết biểu thức biểu thị thời gian ô tô (tính bằng giờ) chạy hết quãng đường 120 km
b) Tính thời gian ô tô đi được 120 km trong trường hợp vận tốc của ô tô là 60km/h
Bài 23 :
Một ngân hàng huy động vốn với mức lãi suất một năm là x%. Để sau một năm, người gửi lãi a đồng thì người đó phải gửi vào ngân hàng số tiền là:
A. \(\frac{{100{\rm{a}}}}{x}\) (đồng)
B. \(\frac{a}{{x + 100}}\) (đồng)
C. \(\frac{a}{{x + 1}}\) (đồng)
D. \(\frac{{100{\rm{a}}}}{{x + 100}}\) (đồng)
Bài 24 :
Biểu thức nào sau đây là phân thức?
-
A.
\(\frac{x}{0}\)
-
B.
\(\frac{{x + y}}{{\frac{1}{y}}}\)
-
C.
\(\frac{{{x^2} + y}}{{\frac{1}{2}y}}\)
-
D.
\(\frac{1}{{\frac{{{x^2} - {y^2}}}{{xy}}}}\)
Bài 25 :
Biểu thức nào sau đây không phải là phân thức đại số?
-
A.
\( \frac{2}{x}\)
-
B.
\( \frac{x}{x+1}\)
-
C.
\(x^{2}-4\)
-
D.
\( \frac{x+1}{0}\)
Bài 26 :
Biểu thức nào sau đây không phải là phân thức đại số?
-
A.
\(\frac{1}{x}\).
-
B.
\(x\).
-
C.
\(\frac{0}{x}\).
-
D.
\(\frac{x}{0}\).
Bài 27 :
Viết các phân thức với tử và mẫu lần lượt là:
a) \(2x - 1\) và \(x + 1\)
b) \({x^2} - x\) và \( - 2\)
c) 3 và \(2x + 5\)
Bài 28 :
Biểu thức nào sau đây không phải là phân thức đại số?
A. \(2x + 1\)
B. \(\sqrt 5 \)
C. \(\pi \)
D. \(\sqrt x \)
Bài 29 :
Phân thức nào sau đây có tử thức là \(2x - 1\) và mẫu thức là \({x^2} - 1\)?
A. \(\frac{{{x^2} - 1}}{{2x - 1}}\).
B. \(\frac{{2x - 1}}{{{x^2} + 1}}\).
C. \(\frac{{2x - 1}}{{{x^2} - 1}}\).
D. \(\frac{{{x^2} - 1}}{{2x + 1}}\).
Bài 30 :
Viết tử thức và mẫu thức của phân thức \(\frac{{5x - 2}}{3}\).


















Danh sách bình luận