Cho một mảnh vườn hình chữ nhật có chu vi là \(80\) mét với chiều dài bằng x mét. Hãy viết biểu thức biểu thị diện tích mảnh vườn. Tính diện tích mảnh vườn khi \(x = 25\)m.
Bước 1: Biểu diễn các đại lượng khác theo ẩn đã cho.
Bước 2: Biểu diễn mối quan hệ giữa các đại lượng theo ẩn bằng các phép toán.
Nửa chu vi của mảnh vườn là \(80:2 = 40\) m.
Chiểu rộng của mảnh vườn là \(40 - x\) m.
Diện tích mảnh vườn là \(x.\left( {40 - x} \right)\) m2
Khi \(x = 25\) ta có \(25.\left( {40 - 25} \right) = 375\) m2.

Các bài tập cùng chuyên đề
Bài 1 :
Cho đa thức \(A = {x^4} - 4{x^3} + x - 3{x^2} + 1.\) Tính giá trị của \(A\) tại \(x = - 2.\)
-
A.
\(A = - 35\)
-
B.
\(A = 53\)
-
C.
\(A = 33\)
-
D.
\(A = 35\)
Bài 2 :
Mỗi số thực có phải một đa thức không? Tại sao?
Bài 3 :
Hãy liệt kê các hạng tử của đa thức \(B = 2{x^4} - 3{x^2} + x + 1\)
Bài 4 :
Các biểu thức 2y + 5; \(2{x^2} - 4x + 7\) được gọi là gì?
Bài 5 :
Trong các biểu thức đại số sau, biểu thức nào không chứa phép tính cộng, phép tính trừ?
\(3{x^2}\); 6 – 2y ; 3t; \(3{t^2} - 4t + 5\); -7
\(3{u^4} + 4{u^2}\); \( - 2{z^4}\); 1; \(2021{y^2}\)
Bài 6 :
Hãy cho biết biểu thức nào sau đây là đa thức một biến:
M = 3; N = 7x; P = \(10 - {y^2} + 5y\); Q = \(\dfrac{{4t - 7}}{3}\); R = \(\dfrac{{2x - 5}}{{1 + {x^2}}}\)
Bài 7 :
Diện tích của một hình chữ nhật được biểu thị bởi đa thức P(x) = \(2{x^2} + 4x\). Hãy tính diện tích của hình chữ nhật ấy khi biết x = 3cm.
Bài 8 :
Tính giá trị của đa thức \(M(t)= - 5{t^3} + 6{t^2} + 2t + 1\) khi \(t = -2\).
Bài 9 :
Quãng đường một chiếc ô tô đi từ A đến B được tính theo biểu thức s = 16t, trong đó s là quãng đường tính bằng mét và t là thời gian tính bằng giây. Tính quãng đường ô tô đi được sau 10 giây.
Bài 10 :
Hãy cho biết biểu thức nào sau đây là đa thức một biến
A = -32;
B = 4x + 7;
M = \(15 - 2{t^3} + 8t\);
N = \(\dfrac{{4 - 3y}}{5}\);
Q = \(\dfrac{{5x - 1}}{{3{x^2} + 2}}\)
Bài 11 :
Tính giá trị của các đa thức sau:
a) P(x) = \(2{x^3} + 5{x^2} - 4x + 3\) khi x = -2
b) Q(y) = \(2{y^3} - {y^4} + 5{y^2} - y\) khi y = 3
Bài 12 :
Một chiếc ca nô đang chạy với tốc độ v = 16 + 2t (v theo đơn vị mét/giây, t là thời gian tính theo đơn vị giây). Tính tốc độ ca nô với t = 5
Bài 13 :
Cho \(A = {x^2}y + 2xy - 3{y^2} + 4\). Tính giá trị của biểu thức A khi x = -2, y = 3.
Bài 14 :
Trong các biểu thức sau, biểu thức nào là đa thức một biến ?
\(3 + 6y\); \(7{x^2} + 2x - 4{x^4} + 1\); \(\dfrac{2}{{x + 1}}\); \(\dfrac{1}{3}x - 5\).
Bài 15 :
Hãy viết một đa thức một biến bậc ba có 3 số hạng.
Bài 16 :
a) Viết biểu thức biểu thị:
- Quãng đường ô tô đi được trong thời gian x (h), nếu vận tốc là 60 km/h;
- Tổng diện tích của các hình: hình vuông có độ dài cạnh là 2x cm; hình chữ nhật có các kích thước là 3 cm và x cm; hình thoi có độ dài hai đường chéo là 4 cm và 8 cm.
b) Các biểu thức trên có bao nhiêu biến? Mỗi số hạng xuất hiện trong biểu thức có dạng như thế nào?
Bài 17 :
Biểu thức nào sau đây là đa thức một biến?
a) \({x^2} + 9;\)
b) \(\dfrac{2}{{{x^2}}} + 2x + 1;\)
c) \(3x + \dfrac{2}{5}y.\)
Bài 18 :
a) Tính giá trị của biểu thức đại số \(3x - 2\) tại x = 2.
b) Tính giá trị của đa thức P(x) = \( - 4x + 6\) tại x = – 3.
Bài 19 :
Cho đa thức \(P(x) = {x^2} - 3x + 2\). Tính P(1), P(2).
Bài 20 :
Theo tiêu chuẩn của Tổ chức Y tế Thế giới (WHO), đối với bé giá, công thức tính cân nặng tiêu chuẩn là \(C = 9 + 2(N - 1)\) (kg), công thức tính chiều cao tiêu chuẩn là \(H = 75 + 5(N - 1)\) (cm), trong đó N là số tuổi của bé gái.
(Nguồn: http://sankom.vn)
a) Tính cân nặng chuẩn, chiều cao chuẩn của một bé gái 3 tuổi.
b) Một bé gái 3 tuổi nặng 13,5 kg và cao 86 cm. Bé gái đó có đạt tiêu chuẩn về cân nặng và chiều cao của Tổ chức Y tế Thế giới hay không?
Bài 21 :
Nhà bác học Galileo Galilei (1564 – 1642) là người đầu tiên phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian chuyển động. Quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) được biểu diễn gần đúng bởi công thức \(y = 5{x^2}\). Trong một thí nghiệm vật lí, người ta thả một vật nặng từ độ cao 180 m xuống đất (coi sức cản của không khí không đáng kể).
a) Sau 3 giây thì vật nặng còn cách mặt đất bao nhiêu mét?
b) Khi vật nặng còn cách mặt đất 100 m thì nó đã rơi được thời gian bao lâu?
c) Sau bao lâu thì vật chạm đất?
Bài 22 :
Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.
a) \( - 7x + 5\);
b) \(2021{x^2} - 2022x + 2023\);
c) \(2{y^3} - \dfrac{3}{{y + 2}} + 4\);
d) \( - 2{t^m} + 8{t^2} + t - 1\), với m là số tự nhiên lớn hơn 2.
Bài 23 :
Tính giá trị của biểu thức:
a) \(A = - 5a - b - 20\)tại \(a = - 4,b = 18\);
b) \(B = - 8xyz + 2xy + 16y\)tại \(x = - 1,y = 3,z = - 2\);
c) \(C = - {x^{2021}}{y^2} + 9{x^{2021}}\) tại \(x = - 2,y = - 3\).
Bài 24 :
Một doanh nghiệp kinh doanh cà phê nhận thấy: Sau khi rang xong, khối lượng cà phê giảm 12% so với trước khi rang.
a) Tìm số thích hợp cho ? ở bảng sau:
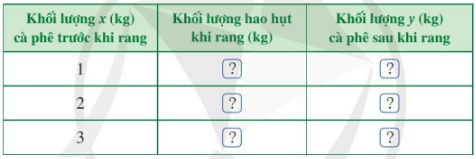
b) Tìm công thức chỉ mối liên hệ giữa x và y.
c) Để có được 2 tấn cà phê sau khi rang thì doanh nghiệp cần sử dụng bao nhiêu tấn cà phê trước khi rang?
Bài 25 :
Một công ty du lịch tổ chức đi tham quan cho một nhóm khách 50 người với mức giá 400 nghìn đồng/người. Công ty đặt ra chính sách khuyến mãi như sau: Sẽ giảm giá cho mỗi người 10 nghìn đồng khi cứ có thêm 1 khách tham gia ngoài 50 khách trên.
a) Giả sử số khách tham gia thêm là x (x < 40). Tính số tiền mà công ty thu được theo x.
b) Nếu số khách tăng thêm là 10 người thì số tiền công ty thu được là tăng hay giảm so với số tiền thu được chỉ với 50 khách ban đầu?
Bài 26 :
Trong các biểu thức sau đây, biểu thức nào là đa thức một biến?
a) \(\frac{{{x^2}}}{{\sqrt 3 }} - \sqrt 3 \);
b) \(\sqrt {2x} \);
c) \(\left( {1 - \sqrt 2 } \right){x^3} + 2\);
d) \(x + \frac{1}{x}\)
Bài 27 :
Biểu thức nào sau đây không là đa thức một biến?
A. \(\sqrt 3 \)
B. -x
C. \(x + \dfrac{{ - 1}}{x}\)
D. \(\dfrac{x}{{\sqrt 2 }} - 1\)
Bài 28 :
Hãy cho biết biểu thức nào sau đây là đa thức một biến:
\(A = - 4\); \(B = 2t + 9\); \(C = \frac{{3x - 4}}{{2x + 1}}\); \(N = \frac{{1 - 2y}}{3}\); \(M = 4 + 7y - 2{y^3}\)
Bài 29 :
Hãy tính giá trị của các đa thức:
a) \(P\left( x \right) = - 3{x^3} + 8{x^2} - 2x + 1\) khi \(x = - 3\).
b) \(Q\left( y \right) = 7{y^3} - 6{y^4} + 3{y^2} - 2y\) khi \(y = 2\).
Bài 30 :
Trong môn bóng chuyền, một cú phát bóng có thể được mô tả bởi biểu thức \(h = - 4,9{t^2} + 3,8t + 1,6\), trong đó h là chiều cao của quả bóng sso với mặt sân được tính bằng mét và t là thời gian kể từ khi phát bóng được tính bằng giây. Tính chiều cao h khi \(t = 0,4\)giây.


















Danh sách bình luận