Cho nửa đường tròn \(\left( {O;R} \right)\) có đường kính AB. Trên nửa đường tròn lấy điểm \(C\) sao cho \(AC > BC\). Gọi \(H\) là hình chiếu của \(C\) trên AB
a. Chứng minh rằng \(\angle ACO = \angle BCH\)
b. Chứng minh rằng: \(AB.AC = AC.AH + BC.CH\)
Vận dụng các tính chất hình học chứng minh.
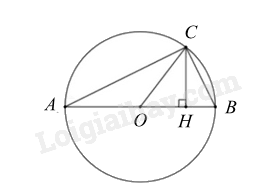
Ta có: $\Delta ACO$ cân tại $O$ (do $OA = OC$)
$\Rightarrow \angle OAC = \angle OCA\,\,\left( 1 \right)$
Vì $C$ thuộc đường tròn đường kính AB nên $\angle ACB = 90^\circ$
Suy ra $\angle ACH + \angle BCH = 90^\circ \,\,\left( 2 \right)$
Lại có: $\angle ACH + \angle CAH = 90^\circ \,\,\left( 3 \right)$ (do $\Delta ACH$ vuông tại $H$)
Từ (1), (2) và (3) suy ra \(\angle ACO = \angle BCH\)
Vậy \(\angle ACO = \angle BCH\)
b) Xét $\Delta ACH$ và $\Delta CBH$ có:
$\begin{array}{l}\angle ACO = \angle BCH\\\angle AHC = \angle BHC = 90^\circ \end{array}$
Suy ra $\Delta ACH\backsim \Delta CBH\left( g.g \right)$
Khi đó \(\frac{{AC}}{{BC}} = \frac{{CH}}{{BH}}\) hay \(AC.BH = BC.CH\)
\(\begin{array}{*{20}{l}}{AC\left( {AB - AH} \right) = BC.CH}\\{AC.AB - AC.AH = BC.CH}\\{AB.AC = AC.AH + BC.CH}\end{array}\)
Vậy \(AB.AC = AC.AH + BC.CH\)

Các bài tập cùng chuyên đề
Bài 1 :
Hình nào dưới đây biểu diễn góc nội tiếp?

-
A.
Hình \(1\)
-
B.
Hình \(2\)
-
C.
Hình $3$
-
D.
Hình \(4\)
Bài 2 :
Vẽ đường tròn tâm O có bán kính bằng 2cm và dây cung AB có độ dài bằng 2cm. Lấy một điểm C tùy ý nằm trên cung lớn AmB (H.9.2).
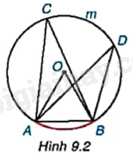
a) Cho biết số đo góc ở tâm AOB và số đo của cung bị chắn AB.
b) Đo góc ACB và so sánh với kết quả của bạn bên cạnh.
c) Lấy điểm D tùy ý nằm trên cung ACB. Đo góc ADB và so sánh với các góc ACB và AOB.
Bài 3 :
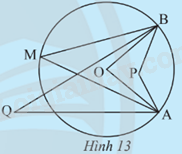
Quan sát Hình 13. Hãy cho biết trong các góc \(\widehat {APB};\widehat {AOB};\widehat {AMB};\widehat {AQB}\), góc nào có đỉnh nằm trên đường tròn (O).
Bài 4 :
Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội tiếp của đường tròn (I) và tính số đo của các góc nội tiếp đó.
Bài 5 :
Cho hai điểm E và F nằm trên đường tròn (O). Có bao nhiêu góc nội tiếp chắn cung EF?
Bài 6 :
Hình nào dưới đây biểu diễn góc nội tiếp?
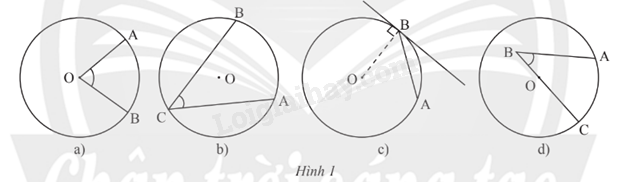
A. Hình 1a
B. Hình 1b
C. Hình 1c
D. Hình 1d
Bài 7 :
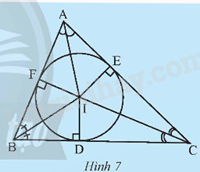
Gọi I là giao điểm ba đường phân giác của tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với các cạnh BC, AC và AB (Hình 7).
a) Chứng minh rằng IE = IF = ID.
b) Vẽ đường tròn tâm I bán kính IE. Có nhận xét gì về vị trí của đường tròn này với ba cạnh của tam giác ABC?
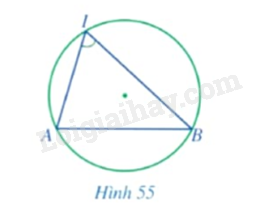
Bài 8 :
Trong Hình 55, đỉnh của góc \(AIB\) có thuộc đường tròn hay không? Hai cạnh của góc chứa hai dây cung nào của đường tròn?
Bài 9 :
Hãy vẽ một đường tròn và hai góc nội tiếp trong đường tròn đó.
Bài 10 :
Quan sát hình ngôi sao năm cánh trong Hình 5.60, đỉnh và cạnh của góc CAD có liên hệ như thế nào với đường tròn khung của lồng đèn ông sao?
Bài 11 :
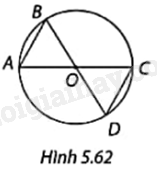
Viết tên các góc nội tiếp của đường tròn (O) được vẽ trong Hình 5.62.
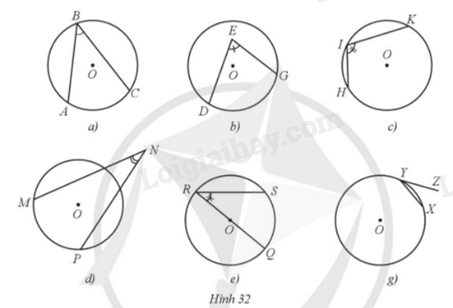
Bài 12 :
Trong các góc \(ABC,DEG,HIK,MNP,QRS,XYZ\) lần lượt ở các hình 32a, 32b, 32c, 32d, 32e, 32g, góc nào là góc nội tiếp, vì sao?
Bài 13 :
Nhận định nào sau đây là sai?
A. Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
B. Góc nội tiếp là góc có đỉnh thuộc đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
C. Góc nội tiếp chắn nửa đường tròn có số đo bằng 90⁰.
D. Số đo của cung AB được kí hiệu là sđAB
Bài 14 :
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm O đường kính AC. Trên tia BH, lấy điểm D sao cho H là trung điểm của đoạn thẳng BD. Nối A với D cắt đường tròn (O) tại E. Chứng minh:
a) CH là tia phân giác của góc ACE;
b) OH // EC.
Bài 15 :
Cho các điểm A, B, C, D thuộc đường tròn tâm O đường kính \(AC = 2\)cm với \(\widehat {CBD} = 55^\circ \) (Hình 51)
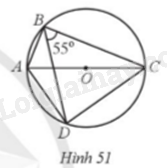
a) Số đo góc CAD là
A. 35°
B. 145°
C. 55°
D. 125°
b) Độ dài đoạn thẳng CD là
A. 2cos55° cm
B. 2sin55° cm
C. 2tan55° cm
D. 2cot55° cm
Bài 16 :
Cho đường tròn (O; R). Lấy A, B, C thuộc đường tròn (O; R). Góc nội tiếp ABC chắn cung nào?
-
A.
AB.
-
B.
AC.
-
C.
OC.
-
D.
BC.
Bài 17 :
Hình nào dưới đây vẽ một góc nội tiếp của đường tròn?
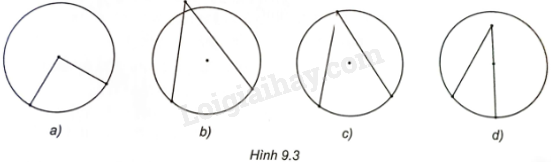
Bài 18 :
Cho tam giác nhọn ABC cân tại đỉnh A. Đường tròn đường kính BC cắt các cạnh AB, AC của tam giác ABC lần lượt tại F và E.
a) Cho BE cắt CF tại H. Chứng minh rằng AH vuông góc với BC.
b) Chứng minh rằng EF song song với BC.


















Danh sách bình luận