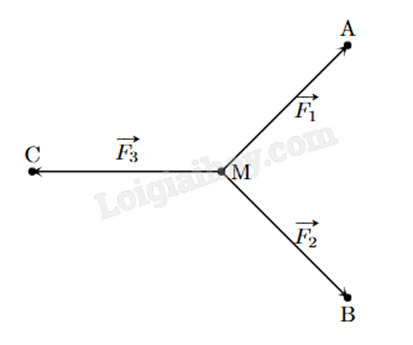
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều bằng 100 N và góc \(\widehat {AMB} = {90^o}\). Tính cường độ của lực \(\overrightarrow {{F_3}} \) (làm tròn đến hàng đơn vị).
Đáp án:
Đáp án:
Sử dụng quy tắc tổng hợp lực, quy tắc hình bình hành.
Dựng hình bình hành AMBD. Vì \(\widehat {AMB} = {90^o}\) nên AMBD là hình vuông.
Áp dụng quy tắc hình bình hành, ta có \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MD} \).
Vì vật đứng yên nên \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).
Từ đó ta suy ra \(\overrightarrow {MD} + \overrightarrow {MC} = \overrightarrow 0 \) hay \(\overrightarrow {MD} = - \overrightarrow {MC} \). Khi đó \(\left| {\overrightarrow {MD} } \right| = \left| { - \overrightarrow {MC} } \right|\) tức MD = MC.
Vì MD là đường chéo của hình vuông cạnh 100 nên \(MD = 100\sqrt 2 \).
Vậy \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MC} } \right| = 100\sqrt 2 \approx 141\) N.

Các bài tập cùng chuyên đề
Bài 1 :
Cho hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác động lên một vật, góc giữa hai vecto bằng \({60^ o }\) và \(\left| {\overrightarrow {{F_1}} } \right| = 6N,\left| {\overrightarrow {{F_2}} } \right| = 8N\). Độ lớn của hợp lực \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) là:
-
A.
5,2
-
B.
12,2
-
C.
14
-
D.
10
Bài 2 :
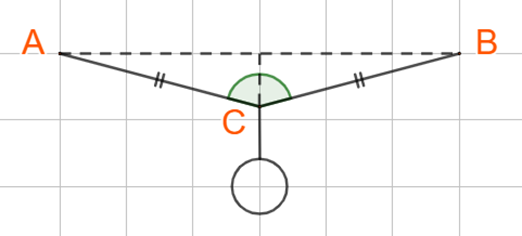
Một chiếc đèn có khối lượng m = 3kg, được treo vào điểm chính giữa của dây AB có khối lượng không đáng kể như hình dưới. Biết \(\widehat {ACB} = {150^o },\) lực kéo của mỗi dây CA, CB là:
-
A.
15
-
B.
27,6
-
C.
38,5
-
D.
56,8
Bài 3 :
Cho tam giác ABC có \(AB = 3,AC = 4,\widehat {BAC} = {120^o}.\) Tính (làm tròn kết quả đến hàng đơn vị):
a) Độ dài cạnh BC và độ lớn góc B.
b) Bán kính đường tròn ngoại tiếp
c) Diện tích của tam giác
d) Độ dài đường cao xuất phát từ A
e) \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AM} .\overrightarrow {BC} \) với M là trung điểm của BC.
Bài 4 :
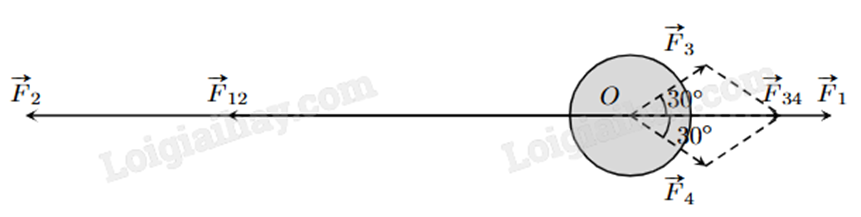
Một vật đang ở vị trí O chịu hai lực tác dụng ngược chiều nhau là \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \), trong đó độ lớn lực \(\overrightarrow {{F_2}} \)lớn gấp ba lần độ lớn lực \(\overrightarrow {{F_1}} \). Để giữ đứng yên, người ta cần tác dụng thêm hai lực \(\overrightarrow {{F_3}} \) và \(\overrightarrow {{F_4}} \), mỗi lực có độ lớn bằng 30 N và hợp với \(\overrightarrow {{F_1}} \) một góc \({30^o}\). Tính tổng độ lớn của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) (làm tròn kết quả đến hàng phần mười).
Bài 5 :
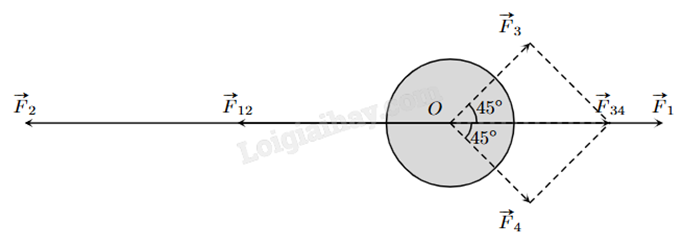
Một vật đang ở vị trí O chịu hai lực tác dụng ngược chiều nhau là \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \), trong đó độ lớn lực \(\overrightarrow {{F_2}} \) lớn gấp đôi độ lớn lực \(\overrightarrow {{F_1}} \). Người ta muốn vật dừng nên cần tác dụng vào vật hai lực \(\overrightarrow {{F_3}} \) và \(\overrightarrow {{F_4}} \) có phương hợp với lực \(\overrightarrow {{F_1}} \) các góc \({45^o}\) như hình vẽ, chúng có độ lớn bằng nhau và bằng 20 N. Tính tổng độ lớn của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) (làm tròn kết quả đến hàng phần mười).
Bài 6 :
Trong mặt phẳng Oxy cho các điểm A(-1;2), B(5;8). Điểm \(M \in Ox\) sao cho tam giác MAB vuông tại A. Diện tích tam giác MAB bằng bao nhiêu?


















Danh sách bình luận