Giá trị sổ sách là giá trị của tài sản mà một công ty sử dụng để tạo ra bảng cân đối kế toán của mình. Một số công ty khấu hao tài sản của họ bằng cách sử dụng phương pháp khấu hao đường thẳng để giá trị của tài sản giảm đi một lượng cố định mỗi năm. Mức suy giảm phụ thuộc vào thời gian sử dụng hữu ích mà công ty đặt vào tài sản. Giả sử rằng một công ty vận tải vừa mua một số ô tô mới với giá 640 triệu đồng một chiếc. Công ty lựa chọn khấu hao từng chiếc xe theo phương pháp khấu hao đường thẳng trong vòng 8 năm. Điều này có nghĩa là sau mỗi năm, mỗi chiếc xe giảm giá \(640:8 = 80\) triệu đồng.

a) Tìm hàm số bậc nhất biểu thị giá trị số sách V (tính theo triệu đồng) của mỗi chiếc ô tô theo tuổi x (năm) của nó.
b) Vẽ đồ thị hàm số bậc nhất tìm được ở câu a.
c) Giá trị sổ sách của mỗi chiếc xe sau 3 năm là bao nhiêu?
d) Khi nào giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng?
a) Sử dụng khái niệm hàm số bậc nhất để tìm hàm số: Hàm số bậc nhất là hàm số cho bởi công thức \(y = ax + b,\) trong đó a, b là các số cho trước và \(a \ne 0\)
b) Sử dụng kiến thức về cách vẽ đồ thị hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) để vẽ các đồ thị
+ Khi \(b = 0\) thì \(y = ax\). Đồ thị của hàm số \(y = ax\) là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a)
+ Khi \(b \ne 0\), ta thường xác định hai điểm đặc biệt trên đồ thị là giao điểm của đồ thị với hai trục tọa độ như sau:
- Cho \(x = 0\) thì \(y = b\), ta được điểm P(0; b) thuộc trục tung Oy.
- Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( { - \frac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số \(y = ax + b\)
c, d) Sử dụng giá trị của hàm số để tính: Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có\(y = f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).
a) Hàm số bậc nhất biểu thị giá trị số sách V (tính theo triệu đồng) của mỗi chiếc ô tô theo tuổi x (năm) của nó là: \(V = 640 - 80x = - 80x + 640\) (triệu đồng)
b) Đồ thị hàm số \(y = V = - 80x + 640\) đi qua 2 điểm \(\left( {0;640} \right)\) và \(\left( {8;0} \right)\)
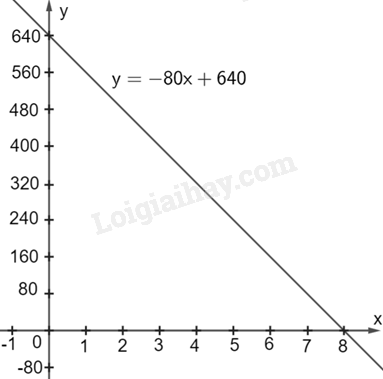
c) Với \(x = 3\) ta có: \(V = - 80.3 + 640 = 400\) (triệu đồng)
d) Với \(V = 160\) ta có: \(160 = - 80x + 640\)
\(80x = 480\)
\(x = 6\)
Vậy sau 6 năm thì giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng.

Các bài tập cùng chuyên đề
Bài 1 :
Cho hàm số bậc nhất \(y = \frac{{ - 1}}{5}x + 7.\) Điểm nào dưới đây thuộc hàm số đã cho?
-
A.
A(7; 0)
-
B.
B(-7; 0)
-
C.
C(0; 7)
-
D.
\(D\left( {\frac{1}{7};0} \right)\)
Bài 2 :
Cho hàm số bậc nhất \(y = 2x + b.\) Biết rằng điểm M(2; 4) thuộc hàm số trên.
Chọn khẳng định đúng?
-
A.
\(b = 0\)
-
B.
\(b = 1\)
-
C.
\(b = 2\)
-
D.
\(b = - 1\)
Bài 3 :
Cho hàm số bậc nhất \(y = ax + 1\left( {a \ne 0} \right).\) Biết rằng điểm A(1; 7) thuộc hàm số trên.
Trong các điểm M(2; 13), N(13; 2), P(6;0), có bao nhiêu điểm thuộc hàm số trên.
-
A.
0 điểm
-
B.
1 điểm
-
C.
2 điểm
-
D.
3 điểm
Bài 4 :
Cho hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right).\) Biết rằng điểm A(0;1) và điểm B(2; 6) thuộc hàm số trên. Khi đó, hàm số bậc nhất là:
-
A.
\(y = x + \frac{2}{5}\)
-
B.
\(y = \frac{2}{5}x + 1\)
-
C.
\(y = x + \frac{5}{2}\)
-
D.
\(y = \frac{5}{2}x + 1\)
Bài 5 :
Cho hàm số bậc nhất \(y = mx + m + 1\left( {m \ne 0} \right)\), biết rằng điểm A(0; 3) thuộc hàm số đã cho. Nếu điểm M có hoành độ là 6 thuộc hàm số trên thì tọa độ của điểm M là:
-
A.
M(6; 15)
-
B.
M(15; -6)
-
C.
M(-6; 15)
-
D.
M(15; 6)
Bài 6 :
Cho hàm số \(2y + 4x + 6 = 0\left( 1 \right)\). Trong các khẳng định:
Khẳng định 1: Hàm số (1) là hàm số bậc nhất
Khẳng định 2: Điểm thuộc trục tung có tung độ bằng 4 thuộc hàm số (1)
Khẳng định 3: Điểm thuộc trục hoành có hoành độ bằng 4 thuộc hàm số (1)
Số khẳng định sai là:
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Bài 7 :
Cho hàm số \(y = \sqrt 2 \left( {x - 1} \right) + 2x + 1\left( 1 \right).\) Cho các khẳng định:
(1) Hàm số (1) là hàm số bậc nhất
(2) Điểm A(0; 1) thuộc hàm số (1)
(3) Giá trị của hàm số tại \(x = 1\) là 3
Hỏi có bao nhiêu khẳng định đúng?
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Bài 8 :
Cho hàm số bậc nhất\(y = \left( {2m - 1} \right)x + {m^2} + 2\left( 1 \right).\) Biết điểm A thuộc trục hoành có hoành độ bằng 1 thuộc hàm số trên. Khi đó,
-
A.
\(m = 2\)
-
B.
\(m = 0\)
-
C.
\(m = 1\)
-
D.
\(m = - 1\)
Bài 9 :
: Cho hàm số \(y = \left( {{a^2} - 4} \right){x^2} + \left( {b - 3a} \right)\left( {b + 2a} \right)x - 2\) là hàm số bậc nhất khi:
-
A.
\(a = 2;b \ne \left\{ {6; - 4} \right\}\)
-
B.
\(a = - 2;b \ne \left\{ { - 6;4} \right\}\)
-
C.
\(a = 2;b = - 2\)
-
D.
Cả A, B, C đều đúng
Bài 10 :
Cho hai điểm \(A\left( {{x_1};{y_1}} \right),B\left( {{x_2};{y_2}} \right)\) với \({x_1} \ne {x_2};{y_1} \ne {y_2}.\) Nếu hai điểm A, B thuộc hàm số \(y = ax + b\) thì:
-
A.
\(\frac{{y - {y_1}}}{{{y_2} - {y_1}}} = 2\frac{{x - {x_1}}}{{{x_2} - {x_1}}}\)
-
B.
\(\frac{{y - {y_1}}}{{{y_2} - {y_1}}} = \frac{{x - {x_1}}}{{{x_2} - {x_1}}}\)
-
C.
\(2\frac{{y - {y_1}}}{{{y_2} - {y_1}}} = \frac{{x - {x_1}}}{{{x_2} - {x_1}}}\)
-
D.
\(\frac{{y - {y_1}}}{{{y_2} - {y_1}}} = \frac{{ - x - {x_1}}}{{{x_2} - {x_1}}}\)
Bài 12 :
Cho đường thẳng \(y = mx + m + 1\;\;\;\left( 1 \right)\) (m là tham số). Đường thẳng (1) luôn đi qua một điểm cố định mới mọi giá trị của m. Điểm cố định đó là:
-
A.
(1; -1)
-
B.
(1; 1)
-
C.
(-1; -1)
-
D.
(-1; 1)
Bài 13 :
Đồ thị hàm số bậc nhất \(y = {\rm{ax + b}}\left( {a \ne 0} \right)\)có tính chất gì?
Bài 14 :
Vẽ đồ thị của mỗi hàm số sau:
a) y = 3x
b) y = 2x + 2
Bài 15 :
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về hai đường thẳng d là đồ thị của hàm số y = ax + b \(\left( {a \ne 0} \right)\)?
a) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng \( - \dfrac{b}{a}\).
b) Đường thẳng d cắt trục tung tại điểm có tung độ bằng \( - \dfrac{b}{a}\)
c) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng b.
d) Đường thẳng d cắt trục tung tại điểm có tung độ bằng b.
Bài 16 :
Vẽ đồ thị các hàm số \(y = 3{\rm{x}};y = 3{\rm{x}} + 4;y = - \dfrac{1}{2}x;y = - \dfrac{1}{2}x + 3\) trên cùng một mặt phẳng tọa độ.
Bài 17 :
a) Vẽ đường thẳng y = 2x -1 trên mặt phẳng tọa độ
b) Xác định đường thẳng y = ax + b \(\left( {a \ne 0} \right)\) đi qua điểm M (1; 3) và song song với đường thẳng y = 2x -1. Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
Bài 18 :
Cho hai hàm số: \(y = - \dfrac{1}{2}x + 3;y = 2{\rm{x}} - 2\)
a) Vẽ đồ thị của hai hàm số đó trên cùng một mặt phẳng tọa độ.
b) Gọi A, B lần lượt là giao điểm của hai đường thẳng \(y = - \dfrac{1}{2}x + 3;y = 2{\rm{x}} - 2\) với trục hoành và C là giao điểm của hai đường thẳng đó. Tính diện tích của tam giác ABC (đơn vị đo trên các trục là centimét)
Bài 19 :
a) Biết rằng với x = 3 thì hàm số y = 2x + b có giá trị là 11. Tìm b và vẽ đồ thị của hàm số với giá trị b vừa tìm được.
b) Biết rằng đồ thị của hàm số y = ax + 6 đi qua điểm A (-2; 2). Tìm a và vẽ đồ thị hàm số với giá trị a vừa tìm được.
Bài 20 :
Trong các phát biểu sau, phát biểu nào đúng?
a) Để vẽ đồ thị của hàm số \(y = ax + b\left( {a \ne 0,b \ne 0} \right)\), ta có thể xác định hai điểm \(P\left( {0;b} \right)\) và \(Q\left( { - \frac{b}{a};0} \right)\) rồi vẽ đường thẳng đi qua hai điểm đó.
b) Để vẽ đồ thị của hàm số \(y = ax + b\left( {a \ne 0,b \ne 0} \right)\), ta có thể xác định hai điểm \(M\left( { - 1; - a + b} \right)\) và \(N\left( { - \frac{b}{a};b} \right)\) rồi vẽ đường thẳng đi qua hai điểm đó.
c) Để vẽ đồ thị của hàm số \(y = ax + b\left( {a \ne 0,b \ne 0} \right)\), ta có thể xác định hai điểm \(I\left( {1;a + b} \right)\) và \(K\left( { - 2; - 2a + b} \right)\) rồi vẽ đường thẳng đi qua hai điểm đó.
Bài 21 :
Vẽ đồ thị của các hàm số \(y = - x,y = - x - 1,y = - \frac{1}{3}x,y = \frac{1}{3}x + 2\) trên cùng một mặt phẳng tọa độ.
Bài 22 :
Tọa độ giao điểm của hai đường thẳng \({d_1}:y = \frac{{1 - 3x}}{4}\) và \({d_2}:y = - \left( {\frac{x}{3} + 1} \right)\) là:A. \(\left( {0; - 1} \right)\)
B. \(\left( { - \frac{7}{3};2} \right)\)
C. \(\left( {0;\frac{1}{4}} \right)\)
D. \(\left( {3; - 2} \right)\)
Bài 23 :
Trong mặt phẳng tọa độ \(Oxy\), cho các điểm \(A\left( {2;3} \right),B\left( {2; - 4} \right)\). Tìm tọa độ điểm \(C\) sao cho \(C\) nằm trên trục \(Ox\) và \(CA + CB\) đạt giá trị nhỏ nhất.
Bài 24 :
Cho hai hàm số \(y = x + 5;y = - x + 1\).
a) Vẽ đồ thị của hai hàm số đó trên cùng một mặt phẳng tọa độ.
b) Gọi \(A\) là giao điểm của hai đường thẳng \(y = x + 5;y = - x + 1\); \(B,C\) lần lượt là giao điểm của hai đường thẳng đó với trục \(Ox\). Tính diện tích của tam giác \(ABC\) (đơn vị đo trên các trục tọa độ là centimet).
Bài 25 :
Vẽ đồ thị của các hàm số y=−2x+3 và \(y = \frac{1}{2}x\)
Bài 26 :
Vẽ đồ thị của các hàm số sau
a) y = 2x − 6
b) y = −3x + 5
c) \(y = \frac{3}{2}x\)
Bài 27 :
Cho hai hàm số y=2x−1 và y=−x+2
a) Trong cùng mặt phẳng tọa độ Oxy, vẽ đồ thị của hai hàm số đã cho
b) Tìm tọa độ giao điểm của hai đồ thị trên
Bài 28 :
Cho hàm số bậc nhất y=(3−m)x+2m+1
Tìm các giá trị của m để đồ thị của hàm số đã cho là:
a) Đường thẳng đi qua điểm (1;2)
b) Đường thẳng cắt đường thẳng y=x+1 tại một điểm nằm trên trục tung
Bài 29 :
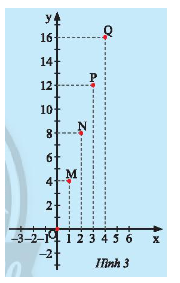
Hùng mua \(x\) mét dây điện và phải trả số tiền là \(y\) nghìn đồng. Giá trị tương ứng giữa \(x\)và \(y\) được cho bởi bảng sau:
Hùng vẽ các điểm \(M\left( {1;4} \right);N\left( {2;8} \right);P\left( {3;12} \right);Q\left( {4;16} \right)\) trên mặt phẳng tọa độ \(Oxy\) như Hình 3. Hãy dùng thước thẳng để kiểm tra các điểm \(O;M;N;P;Q\) có thẳng hàng không.
Bài 30 :
a) Vẽ đồ thị của hàm số: \(y = 0,5x;y = - 3x;y = x\).
b) Các đồ thị sau đây là đồ thị của hàm số nào?




















Danh sách bình luận