Tìm giá trị của tham số m để:
a) \(f\left( x \right) = \left( {2m - 8} \right){x^2} + 2mx + 1\) là một tam thức bậc hai.
b) \(f\left( x \right) = \left( {2m + 3} \right){x^2} + 3x - 4{m^2}\) là một tam thức bậc hai có \(x = 3\) là một nghiệm.
c) \(f\left( x \right) = 2{x^2} + mx - 3\) dương tại \(x = 2\).
a) Sử dụng định nghĩa tam thức bậc hai.
b) Sử dụng định nghĩa tam thức bậc hai.
Thay x = 3 vào phương trình và tìm m.
c) Thay x = 2 vào phương trình rồi tìm m để f(2) > 0.
a) f(x) là tam thức bậc hai khi và chỉ khi \(2m - 8 \ne 0 \Leftrightarrow m \ne 4\)
Vậy để \(f\left( x \right)\) là tam thức bậc hai thì \(m \ne 4\)
b) f(x) là tam thức bậc hai khi và chỉ khi \(2m + 3 \ne 0 \Leftrightarrow m \ne - \frac{3}{2}\)
Mặt khác, \(x = 3\) là nghiệm của f(x) khi và chỉ khi \(f\left( 3 \right) = 0\)
hay \(f\left( 3 \right) = \left( {2m + 3} \right){.3^2} + 3.3 - 4{m^2} = 0 \Leftrightarrow - 4{m^2} + 18m + 36 = 0\)
Suy ra \(m = - \frac{3}{2}\) hoặc \(m = 6\)
Vậy để \(f\left( x \right)\) là tam thức bậc hai và có nghiệm là \(x = 3\) thì \(m = 6\)
c) Hàm số f(x) có \(a = 2 \ne 0\) nên là tam thức bậc hai
\(f\left( x \right) = 2{x^2} + mx - 3\) dương tại \(x = 2\) khi và chỉ khi \(f\left( 2 \right) > 0\)
hay \(f\left( 2 \right) = {2.2^2} + 2m - 3 > 0 \Leftrightarrow m > - \frac{5}{2}\)
Vậy để \(f\left( x \right)\) dương tại \(x = 2\) thì \(m > - \frac{5}{2}\)

Các bài tập cùng chuyên đề
Bài 1 :
Để xây dựng phương án kinh doanh cho một loại sản phẩm, doanh nghiệm tính toán lợi nhuận y (đồng) theo công thức sau: \(y = - 200{x^2} + 92\;000x - 8\;400\;000\), trong đó x là số sản phẩm được bán ra. Như vậy, việc đánh giá hiệu quả kinh doanh loại sản phẩm trên dẫn tới việc xét dấu của \(y = - 200{x^2} + 92\;000x - 8\;400\;000\), tức là ta cần xét dấu của tam thức bậc hai \(f(x) = - 200{x^2} + 92000x - 8400000\).
Làm thế nào để xét dấu của tam thức bậc hai?
Bài 2 :
-
A.
\(f(x) = 2{x^3} + 3{x^2} + 1\)
-
B.
\(f(x) = - {x^2} + 2x - 10\)
-
C.
\(f(x) = x - 4\)
-
D.
\(f(x) = - 7\)
Bài 3 :
Biệt thức ∆ của tam thức bậc hai \(f(x) = - {x^2} - 4x + 5\) bằng
-
A.
34;
-
B.
35;
-
C.
36;
-
D.
37.
Bài 4 :
Hãy cho biết biểu thức nào sau đây là tam thức bậc hai.
\(A = 3x + 2\sqrt x + 1\)
\(B = - 5{x^4} - 3{x^2} + 4\)
\(C = - \frac{2}{3}{x^2} + 7x - 4\)
\(D = {\left( {\frac{1}{x}} \right)^2} + 2.\frac{1}{x} + 3\)
Bài 5 :
Hãy chỉ ra một đặc điểm chung của các biểu thức dưới đây:
\(A = 0,5{x^2}\)
\(B = 1 - {x^2}\)
\(C = {x^2} + x + 1\)
\(D = (1 - x)(2x + 1)\)
Bài 6 :
Tìm biệt thức và nghiệm của các tam thức bậc hai sau:
a) \(f\left( x \right) = 2{x^2} - 5x + 2\)
b) \(g\left( x \right) = - {x^2} + 6x - 9\)
c) \(h\left( x \right) = 4{x^2} - 4x + 9\)
Bài 7 :
Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại \(x = 1\).
a) \(f\left( x \right) = 2{x^2} + x - 1\);
b) \(g\left( x \right) = - {x^4} + 2{x^2} + 1\)
c) \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\)
Bài 8 :
Đa thức nào sau đây là tam thức bậc hai?
a) \(4{x^2} + 3x + 1\)
b) \({x^3} + 3{x^2} - 1\)
c) \(2{x^2} + 4x - 1\)
Bài 9 :
Xác định giá trị của m để các đa thức sau là tam thức bậc hai
a) \(\left( {m + 1} \right){x^2} + 2x + m\)
b) \(m{x^3} + 2{x^2} - x + m\)
c) \( - 5{x^2} + 2x - m + 1\)
Bài 10 :
Tính biệt thức và nghiệm (nếu có) của tam thức bậc hai sau. Xác định dấu của chúng tại \(x = - 2\).
a) \(f\left( x \right) = - 2{x^2} + 3x - 4\).
b) \(g\left( x \right) = 2{x^2} + 8x + 8\).
c) \(h\left( x \right) = 3{x^2} + 7x - 10\).
Bài 11 :
Tìm các giá trị của tham số m để:
a) \(f\left( x \right) = \left( {{m^2} + 9} \right){x^2} + \left( {m + 6} \right)x + 1\) là một tam thức bậc hai có một nghiệm duy nhất.
b) \(f\left( x \right) = \left( {m - 1} \right){x^2} + 3x + 1\) là một tam thức bậc hai có hai nghiệm phân biệt.
c) \(f\left( x \right) = m{x^2} + \left( {m + 2} \right)x + 1\) là một tam thức bậc hai vô nghiệm.
Bài 12 :
Tam thức bậc hai nào có biệt thức \(\Delta = 1\) và hai nghiệm là:\({x_1} = \frac{3}{2}\) và \({x_2} = \frac{7}{4}\)?
A. \(8{x^2} - 26x + 21\)
B. \(4{x^2} - 13x + \frac{{21}}{2}\)
C. \(4{x^2} + 4x - 15\)
D. \(2{x^2} - 7x + 6\)
Bài 13 :
Trong trường hợp nào tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\) có \(\Delta > 0\) và \(a < 0\)?
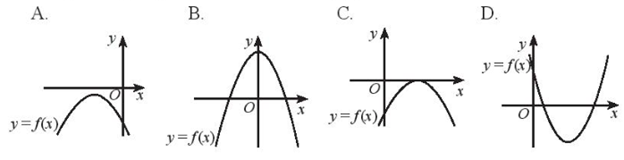
Bài 14 :
Tìm khẳng định đúng trong các khẳng định sau?
-
A.
\(f(x) = 3{x^2} + 2x - 5\) là tam thức bậc hai
-
B.
\(f(x) = 2x - 4\) là tam thức bậc hai
-
C.
\(f(x) = 3{x^3} + 2x - 1\) là tam thức bậc hai
-
D.
\(f(x) = {x^4} - {x^2} + 1\) là tam thức bậc hai
Bài 15 :
Tìm tất cả các giá trị của tham số m để biểu thức \(f(x) = (m - 2){x^2} + 2x - 3\) là một tam thức bậc hai.
-
A.
\(m \in \mathbb{R}\)
-
B.
\(m \ne 2\)
-
C.
\(m > 2\)
-
D.
\(m < 2\)


















Danh sách bình luận