Trong mặt phẳng Oxy cho các điểm A(-1;2), B(5;8). Điểm \(M \in Ox\) sao cho tam giác MAB vuông tại A. Diện tích tam giác MAB bằng bao nhiêu?
Đáp án:
Đáp án:
Sử dụng tích vô hướng để tìm tọa độ điểm M.
Tính MA, AB, từ đó suy ra diện tích tam giác MAB vuông tại A.
Vì \(M \in Ox\) nên \(M({x_M};0)\).
Từ đó ta có \(\overrightarrow {AM} = ({x_M} + 1; - 2)\), \(\overrightarrow {AB} = (6;6)\).
Tam giác MAB vuông tại A nên góc giữa hai vecto \(\overrightarrow {AB} \), \(\overrightarrow {AM} \) bằng \({90^o}\).
Khi đó \(\overrightarrow {AB} .\overrightarrow {AM} = 0 \Rightarrow 6({x_M} + 1) - 12 = 0 \Rightarrow {x_M} = 1\). Vậy M(1;0).
Ta có \(AM = \sqrt {{{(1 + 1)}^2} + {{(0 - 2)}^2}} = 2\sqrt 2 \); \(AB = \sqrt {{{(5 + 1)}^2} + {{(8 - 2)}^2}} = 6\sqrt 2 \).
Vậy \({S_{MAB}} = \frac{1}{2}AM.AB = \frac{1}{2}.2\sqrt 2 .6\sqrt 2 = 12\).

Các bài tập cùng chuyên đề
Bài 1 :
Cho hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác động lên một vật, góc giữa hai vecto bằng \({60^ o }\) và \(\left| {\overrightarrow {{F_1}} } \right| = 6N,\left| {\overrightarrow {{F_2}} } \right| = 8N\). Độ lớn của hợp lực \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) là:
-
A.
5,2
-
B.
12,2
-
C.
14
-
D.
10
Bài 2 :
Một chiếc đèn có khối lượng m = 3kg, được treo vào điểm chính giữa của dây AB có khối lượng không đáng kể như hình dưới. Biết \(\widehat {ACB} = {150^o },\) lực kéo của mỗi dây CA, CB là:
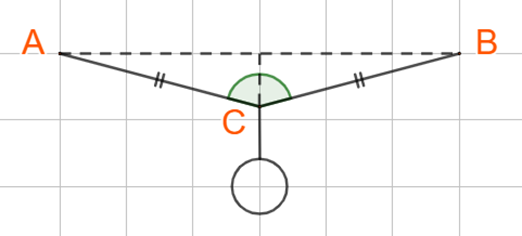
-
A.
15
-
B.
27,6
-
C.
38,5
-
D.
56,8
Bài 3 :
Cho tam giác ABC có \(AB = 3,AC = 4,\widehat {BAC} = {120^o}.\) Tính (làm tròn kết quả đến hàng đơn vị):
a) Độ dài cạnh BC và độ lớn góc B.
b) Bán kính đường tròn ngoại tiếp
c) Diện tích của tam giác
d) Độ dài đường cao xuất phát từ A
e) \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AM} .\overrightarrow {BC} \) với M là trung điểm của BC.
Bài 4 :
Một vật đang ở vị trí O chịu hai lực tác dụng ngược chiều nhau là \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \), trong đó độ lớn lực \(\overrightarrow {{F_2}} \)lớn gấp ba lần độ lớn lực \(\overrightarrow {{F_1}} \). Để giữ đứng yên, người ta cần tác dụng thêm hai lực \(\overrightarrow {{F_3}} \) và \(\overrightarrow {{F_4}} \), mỗi lực có độ lớn bằng 30 N và hợp với \(\overrightarrow {{F_1}} \) một góc \({30^o}\). Tính tổng độ lớn của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) (làm tròn kết quả đến hàng phần mười).
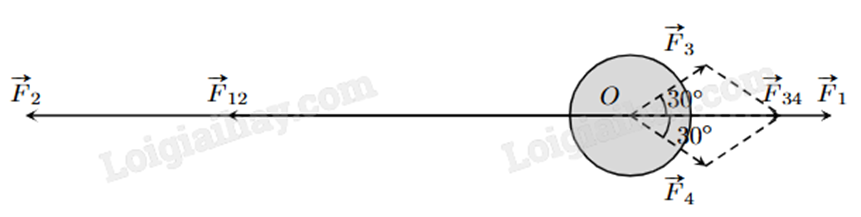
Bài 5 :
Một vật đang ở vị trí O chịu hai lực tác dụng ngược chiều nhau là \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \), trong đó độ lớn lực \(\overrightarrow {{F_2}} \) lớn gấp đôi độ lớn lực \(\overrightarrow {{F_1}} \). Người ta muốn vật dừng nên cần tác dụng vào vật hai lực \(\overrightarrow {{F_3}} \) và \(\overrightarrow {{F_4}} \) có phương hợp với lực \(\overrightarrow {{F_1}} \) các góc \({45^o}\) như hình vẽ, chúng có độ lớn bằng nhau và bằng 20 N. Tính tổng độ lớn của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) (làm tròn kết quả đến hàng phần mười).
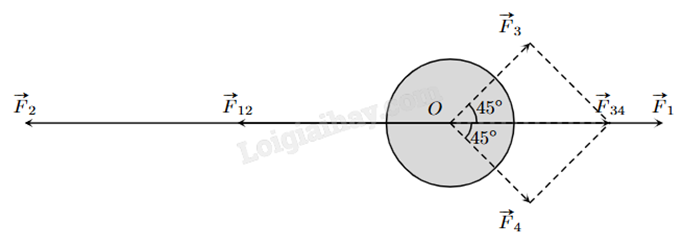
Bài 6 :
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều bằng 100 N và góc \(\widehat {AMB} = {90^o}\). Tính cường độ của lực \(\overrightarrow {{F_3}} \) (làm tròn đến hàng đơn vị).
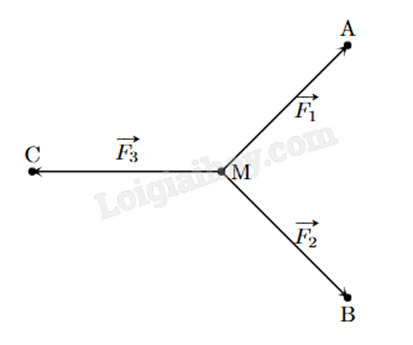


















Danh sách bình luận