Đề bài

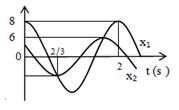
Trên trục x có hai vật tham gia hai dao động điều hoà cùng tần số với các li độ \({x_1}\) và \({x_2}\) có đồ thị biến thiên theo thời gian như hình sau.Vận tốc tương đối giữa hai vật có giá trị cực đại gần nhất với các giá trị nào sau đây?

• A. \(39{\rm{ }}cm/s\)
• B. \(22{\rm{ }}cm/s\)
• C. \(38{\rm{ }}cm/s\)
• D. \(23{\rm{ }}cm/s\)

Phương pháp giải

+ Viết phương trình vận tốc từ phương trình li độ: \(x = A\cos \left( {\omega t + \varphi } \right) \to v =  - A\omega \sin \left( {\omega t + \varphi } \right)\)

+ Sử dụng véc-tơ quay

Lời giải của GV Loigiaihay.com

Từ đồ thị ta có: \(\left\{ \begin{array}{l}{x_1} = 8\cos (\pi t)(cm)\\{x_2} = 6.cos\left( {\pi t + \dfrac{\pi }{3}} \right)cm\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{v_1} =  - 8\pi \sin \pi t\,\,\,(cm/s)\\{v_2} =  - 6\pi .sin\left( {\pi t + \dfrac{\pi }{3}} \right)\,\,(cm/s)\end{array} \right.\)

Vận tốc tương đối của vật 1 đối với vật 2 : \({v_{12}} = {\rm{ }}{v_1}-{\rm{ }}{v_2}\)

Dùng vectơ quay ta có :

\(v_{12max}^2 = v_1^2 + v_2^2 - 2{v_1}.{v_2}.\cos \dfrac{\pi }{3} = {\left( {8\pi } \right)^2} + {\left( {6\pi } \right)^2} - 2.{8\pi}.{6\pi}\cos \dfrac{\pi }{3} \Rightarrow {v_{12max}} = 2\pi \sqrt {13} \,(cm/s) \approx 22,65\left( {cm/s} \right)\)

Đáp án : D