Đề bài

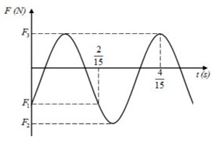
Một con lắc lò xo gồm một vật nhỏ có khối lượng \(m{\rm{ }} = {\rm{ }}200{\rm{ }}g\) và lò xo có độ cứng \(k\) , đang dao động điều hòa theo phương thẳng đứng. Chọn gốc tọa độ ở vị trí cân bằng, chiều dương hướng xuống dưới. Đồ thị biểu diễn sự phụ thuộc của lực đàn hồi theo thời gian được cho như hình vẽ. Biết \({F_1} + {\rm{ }}3{F_2} + {\rm{ }}6{F_3} = {\rm{ }}0\). Lấy \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Tỉ số thời gian lò xo giãn với thời gian lò xo nén trong một chu kì gần giá trị nào nhất sau đây?

• A. \(2,46\)
• B. \(1,38\)
• C. \(1,27\)
• D. \(2,15\)

Phương pháp giải

+ Dùng đường tròn lượng giác

+ Sử dụng công thức tính lực đàn hồi của lò xo: \(F =  - k\left( {\Delta {l_0} + x} \right)\)

Lời giải của GV Loigiaihay.com

Từ đồ thị ta thấy:

Lực đàn hồi tại thời điểm ban đầu: $F = F_1 = - k(Δl_0 + x)$

Lực đàn hồi tại vị trí biên dương: $F = F_2 = - k(Δl_0 + A)$

Lực đàn hồi tại vị trí biên âm: $F = F_3 = - k(Δl_0 – A)$

Gọi \(\Delta t\) là thời gian từ \(t{\rm{ }} = {\rm{ }}0\) đến \(t = \dfrac{2}{{15}}s\)

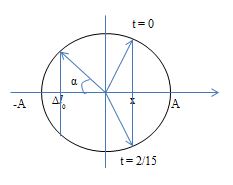
Ta có: \(T + \dfrac{{\Delta t}}{2} = 2\Delta t \Rightarrow \Delta t = \dfrac{{2T}}{3} \Rightarrow x = \dfrac{A}{2}\)

Theo đề bài: \({F_1} + 3{F_2} + 6{F_3} = 0 \Leftrightarrow k\left( {\Delta {l_0} + x} \right) + 3k\left( {\Delta {l_0} + A} \right) + 6k\left( {\Delta {l_0}-A} \right) = 0 \Rightarrow \Delta {l_0} = 0,25A\)

=> Thời gian lo xo nén là : \({t_n} = \dfrac{{2\alpha }}{{360}}T = \dfrac{{151}}{{360}}T = 0,42T \Rightarrow {t_g} = T-{t_n} = 0,58T\)

Tỉ số thời gian giãn và nén trong một chu kì: \(\dfrac{{{t_g}}}{{{t_n}}} = \dfrac{{0,58}}{{0,42}} = 1,381\)

Đáp án : B