Đề bài

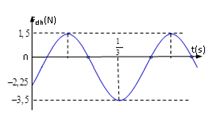
Một con lắc lò xo treo thẳng đứng có độ cứng \(k = 25N/m\) dao động điều hòa theo phương thẳng đứng. Biết trục Ox thẳng đứng hướng xuống, gốc $O$ trùng với $VTCB$. Biết giá trị đại số của lực đàn hồi tác dụng lên vật biến thiên theo đồ thị. Phương trình dao động của vật là

• A. \(x = 8\cos \left( {4\pi t + \dfrac{\pi }{3}} \right)cm.\)
• B. \(x = 10\cos \left( {5\pi t - \dfrac{{2\pi }}{3}} \right)cm.\)
• C. \(x = 10\cos \left( {5\pi t + \dfrac{\pi }{3}} \right)cm.\)
• D. \(x = 8\cos \left( {4\pi t - \dfrac{\pi }{3}} \right)cm.\)

Phương pháp giải

+ Đọc đồ thị $F – t$

+ Sử dụng biểu thức tính lực đàn hồi cực đại, cực tiểu:

- Lực đàn hồi cực đại: \({F_{d{h_{{\rm{max}}}}}} = k\left( {A + \Delta {l_0}} \right)\)

- Lực đàn hồi cực tiểu: \({F_{d{h_{\min }}}} = k\left( {A - \Delta {l_0}} \right)\)

+ Biểu thức của lực đàn hồi: \({F_{dh}} =  - k\left( {\Delta {l_0} + x} \right)\)

+ Xác định thời điểm ban đầu \(t = 0\) thì \(F = ?\)

Lời giải của GV Loigiaihay.com

Từ đồ thị ta có hệ:

\(\begin{array}{l}\left\{ \begin{array}{l}k(A - \Delta {l_0}) = 1,5\\k(A + \Delta {l_0}) = 3,5\end{array} \right.\\ \Rightarrow A = \dfrac{5}{2}\Delta {l_0}\\ \Rightarrow \left\{ \begin{array}{l}\Delta {l_0} = 0,04m = 4cm\\A = 0,1m = 10cm\end{array} \right.\\ \Rightarrow \omega  = \sqrt {\dfrac{g}{{\Delta {l_0}}}}  = 5\sqrt {10}  \approx 5\pi (rad/s)\end{array}\)

Biểu thức của lực đàn hồi có dạng: \(F =  - k(\Delta {l_0} + x) =  - 1 - 2,5\cos (5\pi t + \varphi )N\)

Lúc \(t = 0,{\rm{ }}F =  - 2,25cos\varphi  =  - 1,25 \Rightarrow cos\varphi  = \dfrac{1}{2} \Rightarrow \varphi  = \dfrac{\pi }{3}\)

Vậy phương trình dao động của vật là: \(x = 10\cos \left( {5\pi t + \dfrac{\pi }{3}} \right)cm\)

Đáp án : C