Với mỗi hàm số bậc hai cho dưới đây: \(y = f(x) = - {x^2} - x + 1\); \(y = g(x) = {x^2} - 8x + 8\).
Hãy thực hiện các yêu cầu sau:
a) Viết lại hàm số bậc hai dưới dạng \(y = a{(x - h)^2} + k\).
b) Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số.
c) Vẽ đồ thị của hàm số.
a) Ta có:
\(y = f(x) = - {x^2} - x + 1 \Leftrightarrow f(x) = - \left( {{x^2} + x + \frac{1}{4}} \right) + \frac{5}{4} \Leftrightarrow f(x) = - {\left( {x + \frac{1}{2}} \right)^2} + \frac{5}{4}\)
\(y = g(x) = {x^2} - 8x + 8 \Leftrightarrow g(x) = {x^2} - 8x + 16 - 8 \Leftrightarrow g(x) = {(x - 4)^2} - 8\)
b) Ta có:
\(f(x) = - {\left( {x + \frac{1}{2}} \right)^2} + \frac{5}{4} \le \frac{5}{4}\) \( \Rightarrow \) GTLN của f(x) là \(\frac{5}{4}\) đạt được khi \(x = - \frac{1}{2}\)
\(g(x) = {(x - 4)^2} - 8 \ge - 8 \Rightarrow \) GTNN của g(x) là -8 đạt được khi x = 4
c)
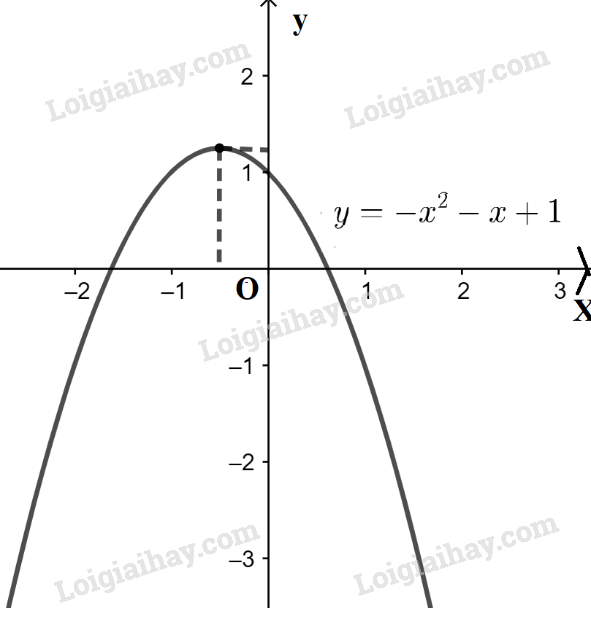
- Đồ thị hàm số \(y = - {x^2} - x + 1\) là đường parabol có a = -1 < 0 nên có bề lõm quay xuống dưới.
Đỉnh \(I\left( { - \frac{1}{2};\frac{5}{4}} \right)\), trục đối xứng x = \( - \frac{1}{2}\). Giao điểm của parabol với trục Oy là điểm (0 ; 1) và cắt trục Ox tại 2 điểm có hoành độ \(x = \frac{{ - 1 - \sqrt 5 }}{2}\) và \(x = \frac{{ - 1 + \sqrt 5 }}{2}\)
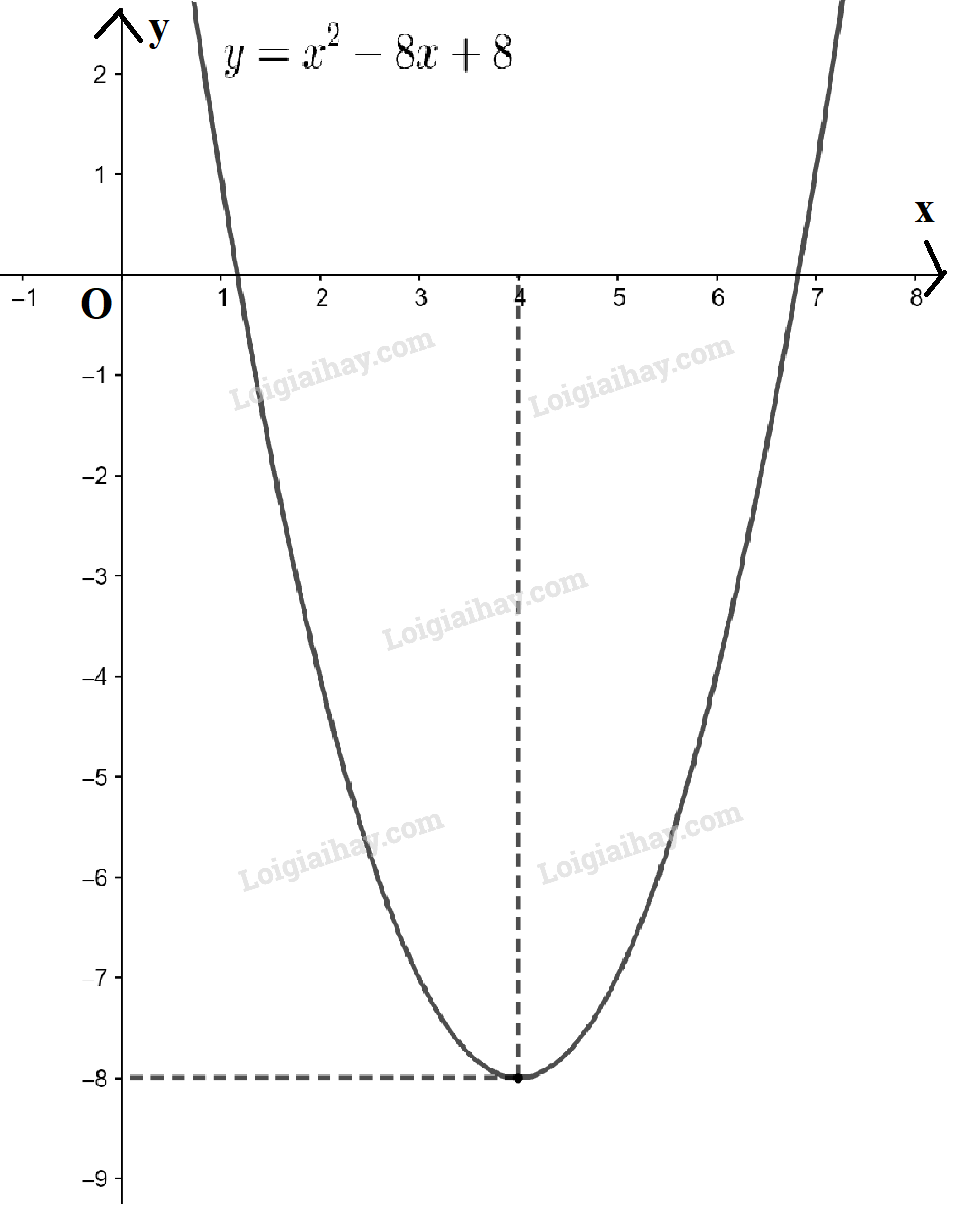
- Đồ thị hàm số \(y = {x^2} - 8x + 8\) là đường parabol có a = 1 > 0 nên có bề lõm quay lên trên
Đỉnh \(I(4; - 8)\), trục đối xứng x = 4. Giao điểm của parabol với trục Oy là điểm (0 ; 8) và cắt trục Ox tại 2 điểm có hoành độ \(x = 4 - 2\sqrt 2 \) và \(x = 4 + 2\sqrt 2 \)

Các bài tập cùng chuyên đề
Bài 1 :
Cho đồ thị hàm số bậc hai ở Hình 15.
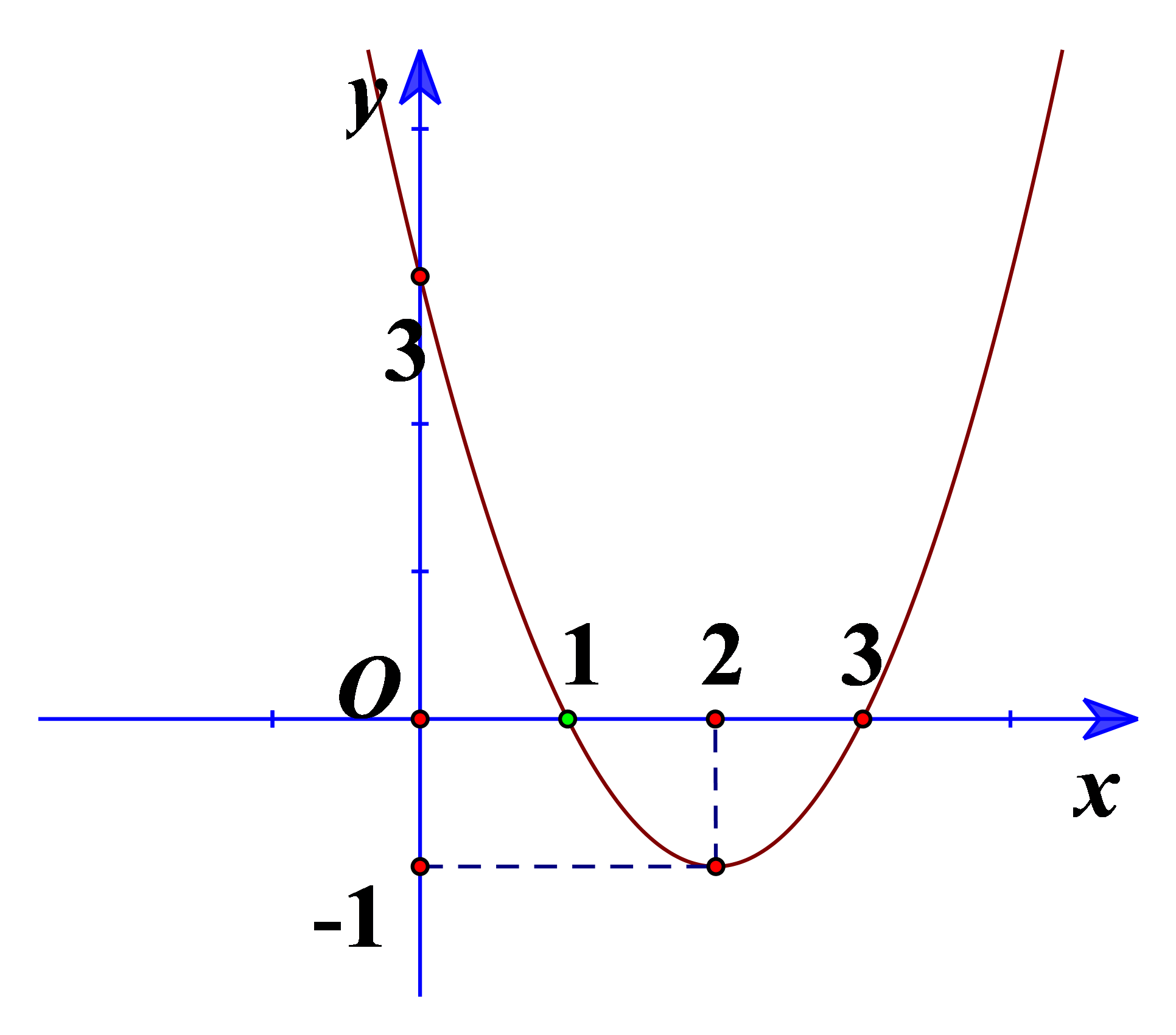
a) Xác định trục đối xứng, tọa độ đỉnh của đồ thị hàm số.
b) Xác định khoảng đồng biến, khoảng nghịch biến của hàm số.
c) Tìm công thức xác định hàm số.
Bài 2 :
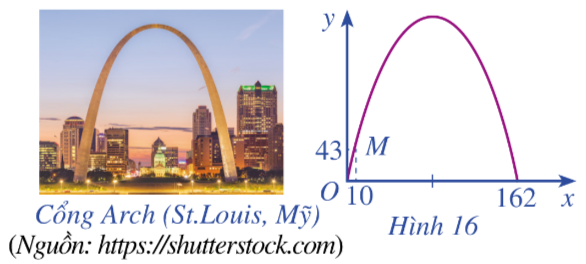
Khi du lịch đến thành phố St. Louis (Mỹ), ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới, đó là cổng Arch. Giả sử ta lập một hệ toạ độ Oxy sao cho một chân cổng đi qua gốc O như Hình 16 (x và y tính bằng mét), chân kia của cổng ở vị trí có toạ độ (162;0). Biết một điểm M trên cổng có toạ độ là (10;43). Tính chiều cao của cổng (tính từ điểm cao nhất trên cổng xuống mặt đất), làm tròn kết quả đến hàng đơn vị.
Bài 3 :
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Bài 4 :
Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.
Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:
- Dây dài nhất là 5 m, dây ngắn nhất là 0,8 m. Khoảng cách giữa các dây bằng nhau.
- Nhịp cầu dài 30 m.
- Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

Bài 5 :
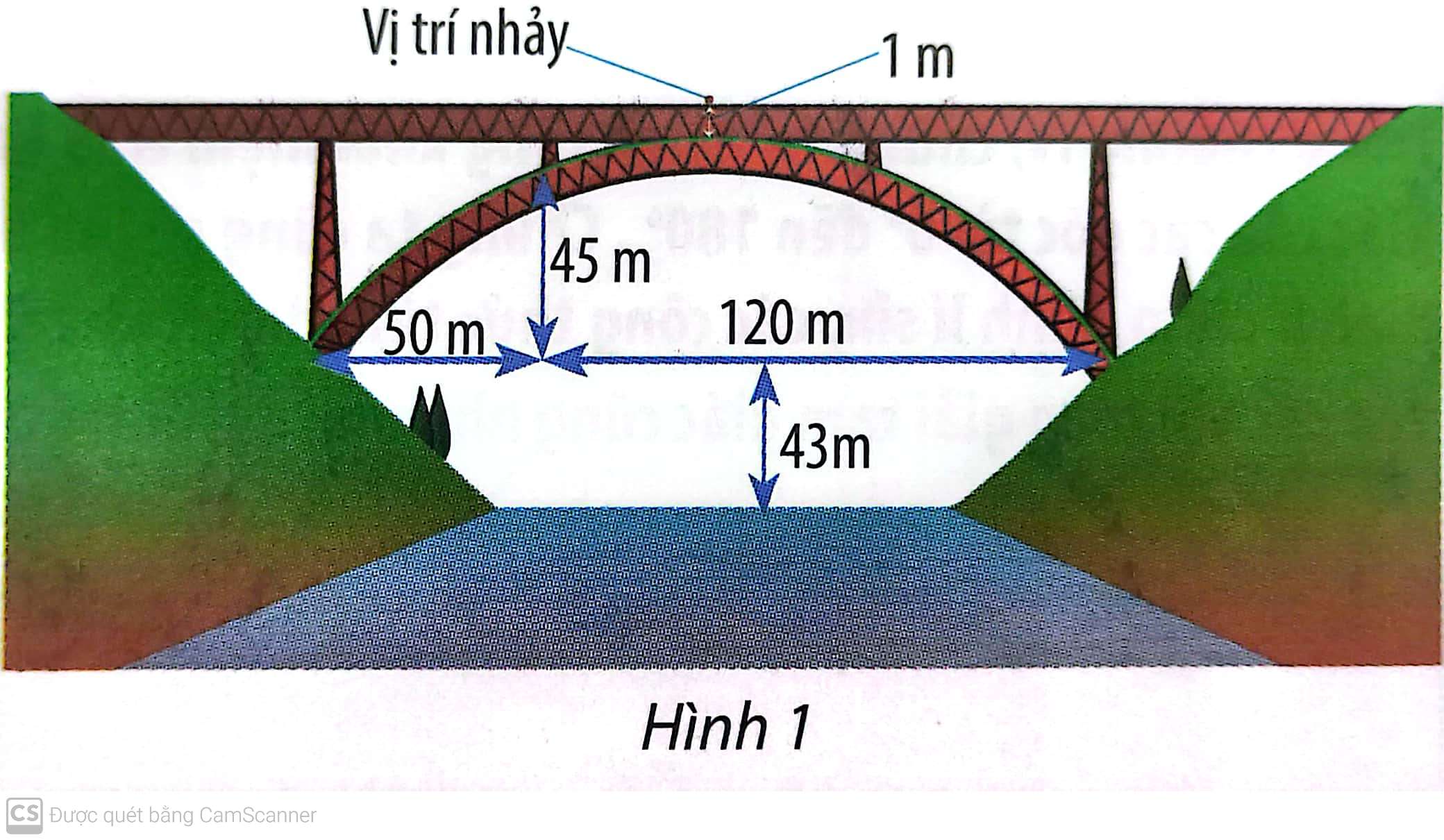
Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn và nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước). Chiếc cầu trong Hình 1 có bộ phận chống đỡ dạng parabol. Một người muốn thực hiện một cú nhày bungee từ giữa cầu xuống với dây an toàn. Người này cần trang bị sợi dây an toàn dài bao nhiêu mét? Biết rằng chiều dài của sợi dây đó bằng một phần ba khoảng cách từ vị trí bắt đầu nhảy đến mặt nước.
Bài 6 :
Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80 m, lúc đó máy bay đang bay với vận tốc 50 m/s. Để thùng hàng cứu trợ rơi đúngvị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí nào? Biết rằng nếu chọn gốc toạ độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì toạ độ của hàng cứu trợ được cho bởi hệ sau:
\(\left\{ \begin{array}{l}x = {v_0}t\\y = h - \frac{1}{2}g{t^2}\end{array} \right.\)
Trong đó, \({v_0}\) là vận tốc ban đầu và h là độ cao tính từ khi hàng rời máy bay.
Lưu ý: Chuyển động này được xem là chuyển động ném ngang.
Bài 7 :
Cho hàm số bậc hai có đồ thị là parabol có đỉnh S , đi qua các điểm A, B, \(C\left( {0; - 1} \right)\) được cho trong hình 10
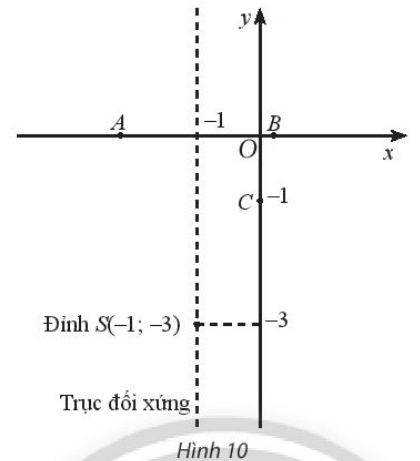
a) Vẽ đồ thị hàm số đã cho
b) Tìm tập giá trị của hàm số và chỉ ra các khoảng biến thiên của hàm số
Bài 8 :
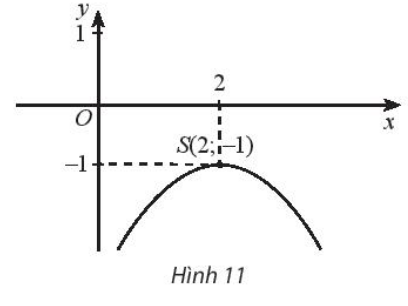
Tìm tập xác định, giá trị lớn nhất của hàm số, tập giá trị và các khoảng biến thiên của hàm số biết đồ thị hàm số là một parabol có đỉnh S như hình 11
Bài 9 :
Hàm số \(y = f\left( x \right) = \left( {x + 2} \right)\left( {x - 2} \right)\) có:
A. Giá trị nhỏ nhất là 4
B. Giá trị lớn nhất là 4
C. Giá trị lớn nhất là \( - 4\)
D. Giá trị nhỏ nhất là \( - 4\)
Bài 10 :
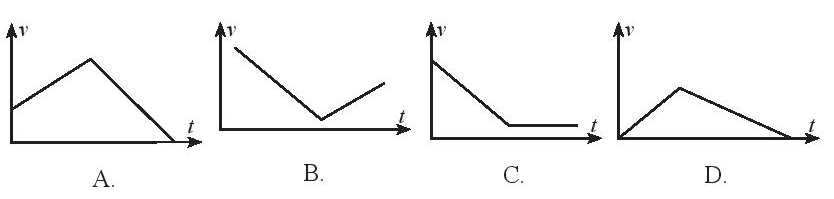
Một viên bi được thả không vận tốc đầu và lăn trên máng nghiêng như hình 1.
Đồ thị nào sau đây phù hợp với sự thay đổi vận tốc của viên bi theo thời gian?
Bài 11 :
Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tập giá trị, khoảng đồng biến, khoảng nghịch biến của nó:
a) \(y = - {x^2} + 6x - 9\)
b) \(y = - {x^2} - 4x + 1\)
c) \(y = {x^2} + 4x\)
d) \(y = 2{x^2} + 2x + 1.\)
Bài 12 :
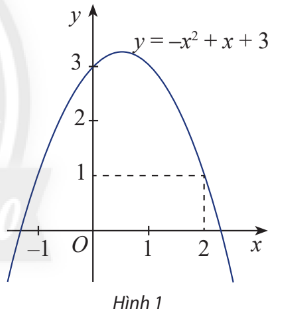
Đồ thị của hàm số \(y = f\left( x \right) = - {x^2} + x + 3\) được biểu diễn trong hình 1.
a) Biểu thức \(f\left( x \right)\) là đa thức bậc mấy?
b) Xác định dấu của \(f\left( 2 \right)\).
Bài 13 :
Cho hàm số \(y = f(x) = a{x^2} + bx + c\) với đồ thị là parabol (P) có đỉnh \(I\left( {\frac{5}{2}; - \frac{1}{4}} \right)\) và đi qua điểm \(A(1;2)\).
a) Biết rằng phương trình của parabol có thể viết dưới dạng \(y = a{(x - h)^2} + k\), tron đó I(h;k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.
b) Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f(x)\).
c) Giải bất phương trình \(f(x) \ge 0\).
Bài 14 :
Cho đồ thị của hai hàm số bậc hai như dưới đây
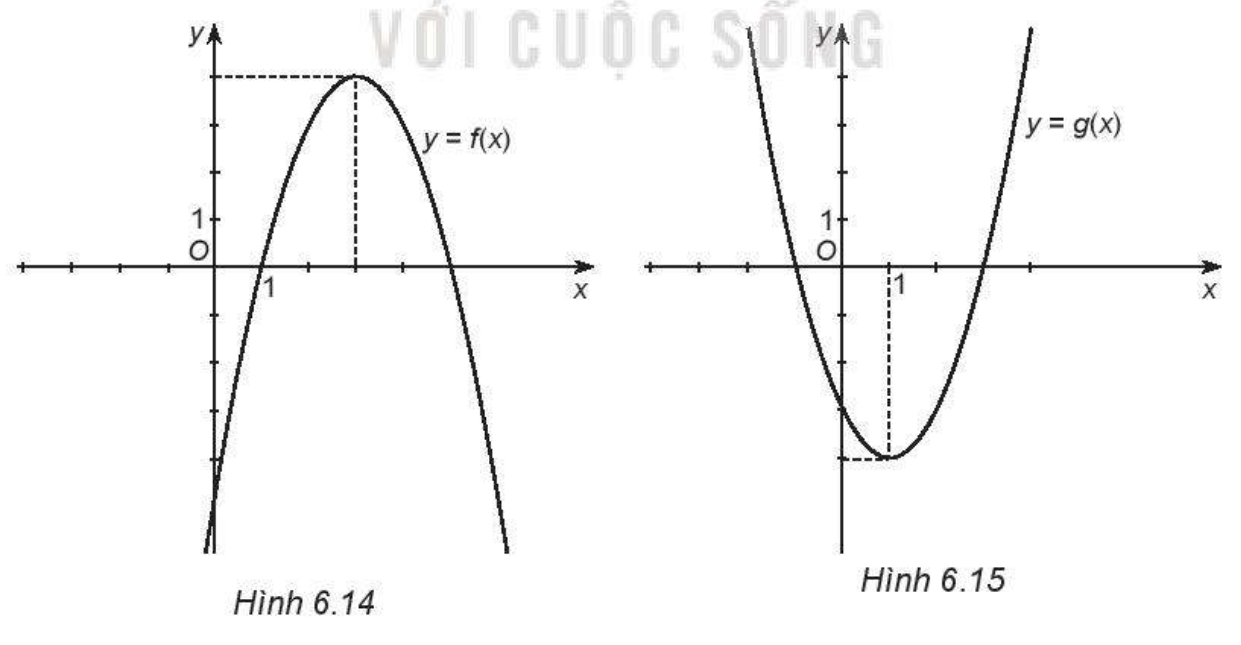
Với mỗi đồ thị, hãy:
a) Tìm tọa độ đỉnh của đồ thị.
b) Tìm khoảng đồng biến và khoảng nghịch biến của hàm số.
c) Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số.
d) Tìm tập xác định và tập giá trị của hàm số.
Bài 15 :
Trong mỗi trường hợp dưới đây, hãy vẽ đồ thị của các hàm số trên cùng một mặt phẳng tọa độ rồi xác định tọa độ giao điểm của chúng.
a) \(y = - x + 3\) và \(y = - {x^2} - 4x + 1\).
b) \(y = 2x - 5\) và \(y = {x^2} - 4x - 1\).
Bài 16 :
Cho hàm số \(y = {x^2} - 2x - 3\). Khẳng định nào sau đây là đúng?
-
A.
Đồ thị hàm số là một đường thẳng
-
B.
Đồ thị hàm số là một parabol
-
C.
Hàm số đồng biến trên \(\mathbb{R}\)
-
D.
Hàm số nghịch biến trên \(\mathbb{R}\)
Bài 17 :
Cho đồ thị hàm số bậc hai y = f(x) có dạng như hình sau:
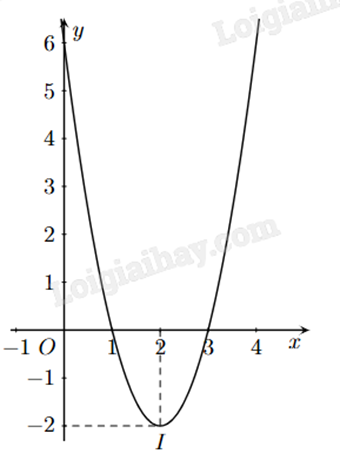
a) Trục đối xứng của đồ thị là đường thẳng x = -2.
b) Đỉnh I của đồ thị hàm số có tọa độ là (2;-2).
c) Đồ thị hàm số đi qua điểm A(0;6).
d) Hàm số đã cho là \(y = 2{x^2} - 2x + 6\).
Bài 18 :
Cho tam thức bậc hai với đồ thị là parabol có đỉnh I(1, 4) và đi qua điểm A(2; 3).
a) Xác định các hệ số a, b, c của tam thức bậc hai f(x).
b) Vẽ parabol này.
c) Từ đồ thị đã vẽ ở câu b), hãy cho biết khoảng đồng biến, khoảng nghịch biến và tập giá trị của hàm số y = f(x).
d) Lập bảng xét dấu để giải bất phương trình \(\frac{{f(x)}}{{x - 2}} \ge 0\).



















Danh sách bình luận