Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông, \(AC\) cắt \(BD\) tại \(O\), \(SO \bot \left( {ABCD} \right)\). Tất cả các cạnh của hình chóp bằng \(a\).
a) Tính góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {SAC} \right)\).
b) Gọi \(\alpha \) là số đo của góc nhị diện \(\left[ {S,CD,A} \right]\). Tính \(\cos \alpha \).
c) Gọi \(d\) là giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\), \(\beta \) là số đo của góc nhị diện \(\left[ {A,d,D} \right]\). Tính \(\cos \beta \).
d*) Gọi \(\gamma \) là số đo góc nhị diện \(\left[ {B,SC,D} \right]\). Tính \(\cos \gamma \).
a) Xác định hình chiếu của \(B\) trên mặt phẳng \(\left( {SAC} \right)\), từ đó tính được góc giữa \(SB\) và \(\left( {SAC} \right)\).
b) Gọi \(N\) là trung điểm của \(CD\). Chứng minh góc phẳng nhị diện của góc nhị diện \(\left[ {S,CD,A} \right]\) là góc \(\widehat {SNO}\). Tính \(\cos \widehat {SNO}\).
c) Chứng minh rằng \(d\) song song với \(AB\) và \(CD\). Gọi \(M\) là trung điểm của \(AB\). Chứng minh rằng góc phẳng nhị diện của góc nhị diện \(\left[ {A,d,D} \right]\) là góc \(\widehat {MSN}\), từ đó tính \(\cos \widehat {MSN}\).
d) Gọi \(E\) là hình chiếu của \(B\) trên \(SC\). Chứng minh góc phẳng nhị diện của góc nhị diện \(\left[ {B,SC,D} \right]\) là góc \(\widehat {BED}\). Tính \(\cos \widehat {BED}\).
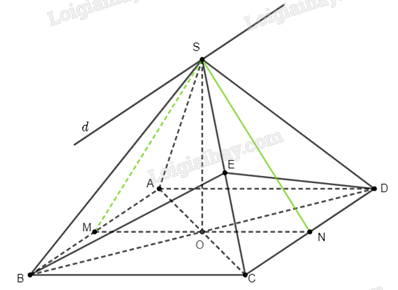
a) Do \(SO \bot \left( {ABCD} \right)\), ta có \(SO \bot OB\). Vì \(ABCD\) là hình vuông nên \(BO \bot AC\). Như vậy \(BO \bot \left( {SAC} \right)\), tức là hình chiếu của điểm \(B\) trên \(\left( {SAC} \right)\). Do đó góc giữa \(SB\) và \(\left( {SAC} \right)\) là góc \(\widehat {BSO}\).
Ta có \(ABCD\) là hình vuông cạnh \(a\), nên \(BD = a\sqrt 2 \).
Tam giác \(SBD\) có \(SB = SD = a\) và \(S{B^2} + S{D^2} = {a^2} + {a^2} = 2{a^2} = B{D^2}\), nên tam giác này là tam giác vuông cân tại \(S\).
Hơn nữa, do \(SO \bot BD\), ta suy ra \(\widehat {BSO} = \widehat {SBO} = {45^o}\).
Như vậy, góc giữa \(SB\) và \(\left( {SAC} \right)\) bằng \({45^o}\).
b) Gọi \(N\) là trung điểm của \(CD\). Do tam giác \(SCD\) đều (\(SC = SD = CD = a\)), ta suy ra \(SN \bot CD\) và \(SN = \sqrt {S{C^2} - C{N^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\).
Do \(O\) là tâm của hình vuông \(ABCD\), ta suy ra \(ON \bot CD\). Như vậy, góc phẳng nhị diện của góc nhị diện \(\left[ {S,CD,O} \right]\) là góc \(\widehat {SNO}\). Hơn nữa do \(O \in \left( {ABCD} \right)\), ta suy ra góc nhị diện \(\left[ {S,CD,O} \right]\) cũng chính là góc nhị diện \(\left[ {S,CD,A} \right]\), tức là \(\alpha = \widehat {SNO}\).
Như vậy \(\cos \alpha = \cos \widehat {SNO} = \frac{{ON}}{{SN}} = \frac{{\frac{a}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{3}\).
c) Ta thấy rằng \(AB\parallel CD\), \(AB \subset \left( {SAB} \right)\), \(CD \subset \left( {SCD} \right)\), \(S \in \left( {SAB} \right) \cap \left( {SCD} \right)\), nên giao tuyến \(d\) của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) đi qua \(S\) và song song với \(AB\) và \(CD\).
Gọi \(M\) là trung điểm của \(AB\). Tam giác \(SAB\) đều (\(SA = AB = SB = a\)) nên \(SM \bot AB\). Mặt khác, do \(d\parallel AB\) nên \(SM \bot d\). Chứng minh tương tự ta cũng có \(SN \bot d\). Suy ra góc phẳng nhị diện của góc nhị diện \(\left[ {M,d,N} \right]\) là góc \(\widehat {MSN}\).
Hơn nữa, do \(AM\parallel d\) và \(DN\parallel d\), ta suy ra góc nhị diện \(\left[ {M,d,N} \right]\) cũng chính là \(\left[ {A,d,D} \right]\), tức là \(\beta = \widehat {MSN}\).
Ta có \(SM = SN = \frac{{a\sqrt 3 }}{2}\), \(MN = a\). Theo định lí cos trong tam giác, ta có:
\(\cos \beta = \cos \widehat {MSN} = \frac{{S{M^2} + S{N^2} - M{N^2}}}{{2SM.SN}} = \frac{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} - {a^2}}}{{2.\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 3 }}{2}}} = \frac{1}{3}\).
d) Gọi \(E\) là hình chiếu của \(B\) trên \(SC\). Theo câu a, ta có \(BD \bot \left( {SAC} \right)\) nên suy ra \(BD \bot SC\). Mà \(BE \bot SC\) nên suy ra \(SC \bot \left( {BDE} \right)\), điều này dẫn tới \(SC \bot DE\).
Như vậy, vì \(BE \bot SC\), \(SC \bot DE\) nên góc phẳng nhị diện của góc nhị diện \(\left[ {B,SC,D} \right]\) là góc \(\widehat {BED}\), tức là \(\gamma = \widehat {BED}\).
Tam giác \(SBC\) đều (\(SB = SC = BC = a\)) và có \(BE \bot SC\), nên ta dễ dàng tính được \(BE = \frac{{a\sqrt 3 }}{2}\). Tương tự, ta cũng có \(DE = \frac{{a\sqrt 3 }}{2}\).
Theo định lí cos trong tam giác, ta có:
\(\cos \gamma = \cos \widehat {BED} = \frac{{B{E^2} + D{E^2} - B{D^2}}}{{2BE.DE}} = \frac{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {a\sqrt 2 } \right)}^2}}}{{2.\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 3 }}{2}}} = \frac{{ - 1}}{3}\).

Các bài tập cùng chuyên đề
Bài 1 :
Trong cửa sổ ở Hình 7.56, cánh và khung cửa là các nửa hình tròn có đường kính 80 cm, bản lề được đính ở điểm chính giữa O của các cung tròn khung và cánh cửa. Khi cửa mở, đường kính của khung và đường kính của cánh song song với nhau và cách nhau một khoảng d; khi cửa đóng, hai đường kính đó trùng nhau. Hãy tính số đo của góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa khi d = 40 cm.

Bài 2 :
Cho hình chóp S.ABC có SA \( \bot \) (ABC), AB = AC = a, \(\widehat {BAC} = {120^0},SA = \frac{a}{{2\sqrt 3 }}.\) Gọi M là trung điểm của BC.
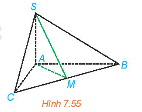
a) Chứng minh rằng \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A].
b) Tính số đo của góc nhị diện [S, BC, A].
Bài 3 :
Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng \(a\sqrt {\frac{5}{{12}}} .\) Tính số đo của góc nhị diện [S, BC, A].
Bài 4 :
Cho hình chóp S.ABC có SA \( \bot \) (ABC). Gọi H là hình chiếu của A trên BC.
a) Chứng minh rằng (SAB) \( \bot \) (ABC) và (SAH) \( \bot \) (SBC).
b) Giả sử tam giác ABC vuông tại A, \(\widehat {ABC} = {30^0},AC = a,SA = \frac{{a\sqrt 3 }}{2}.\) Tính số đo của góc nhị diện [S, BC, A].
Bài 5 :
Cho hình chóp tứ giác đều S.ABCD. Phát biểu nào sau đây là đúng?
A. Số đo của góc nhị diện [S, AB, C] bằng \(\widehat {SBC}\).
B. Số đo của góc nhị diện [D, SA, B] bằng \({90^0}\).
C. Số đo của góc nhị diện [S, AC, B] bằng \({90^0}\).
D. Số đo của góc nhị diện [D, SA, B] bằng \(\widehat {BSD}\).
Bài 6 :
Cho biết kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều với chiều cao 98 m và cạnh đáy 180 m. Tính số đo góc nhị diện tạo bởi mặt bên và mặt đáy.
(Nguồn: https://en.wikipedia.org/wiki/Memphis Pyramid)

Bài 7 :
Cho hình chóp tứ giác đều \(S.ABCD\) với \(O\) là tâm của đáy và có tất cả các cạnh đều bằng \(a\). Xác định và tính góc phẳng nhị diện:
a) \(\left[ {S,BC,O} \right]\);
b) \(\left[ {C,SO,B} \right]\).
Bài 8 :
Cho tứ diện đều \(ABCD\). Vẽ hình bình hành \(BCED\).
a) Tìm góc giữa đường thẳng \(AB\) và \(\left( {BCD} \right)\).
b) Tim góc phẳng nhị diện \(\left[ {A,CD,B} \right];\left[ {A,CD,E} \right]\).
Bài 9 :
Cho hình chóp tứ giác đều \(S.ABCD\) có \(O\) là tâm của đáy và có tất cả các cạnh bằng nhau.
a) Tìm góc giữa đường thẳng \(SA\) và \(\left( {ABCD} \right)\).
b) Tim góc phẳng nhị diện \(\left[ {A,SO,B} \right];\left[ {S,AB,O} \right]\).
Bài 10 :
Cho hình chóp cụt lục giác đều \(ABCDEF.A'B'C'D'E'F'\) với \(O\) và \(O'\) là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là \(a\) và \(\frac{a}{2},OO' = a\)
a) Tìm góc giữa cạnh bên và mặt đáy.
b) Tìm góc phẳng nhị diện \(\left[ {O,AB,A'} \right];\left[ {O',A'B',A} \right]\).
Bài 11 :
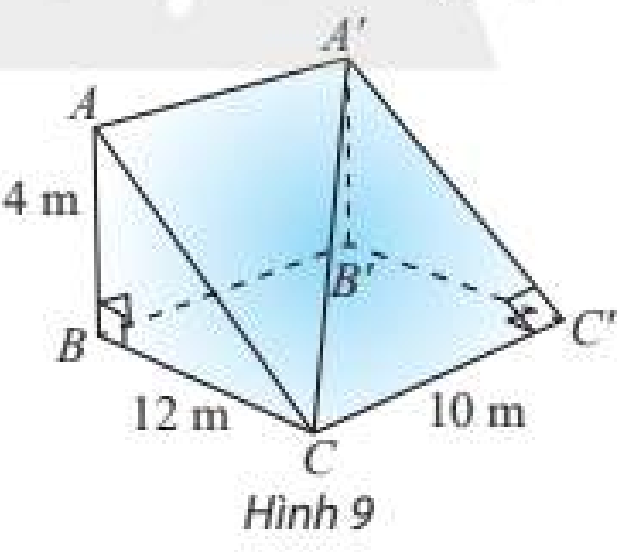
Một con dốc có dạng hình lăng trụ đứng tam giác với kích thước như trong Hình 9.
a) Tính số đo góc giữa đường thẳng \(CA'\) và (CC'B'B).
b) Tính số đo góc nhị diện cạnh \(CC'\).
Bài 12 :
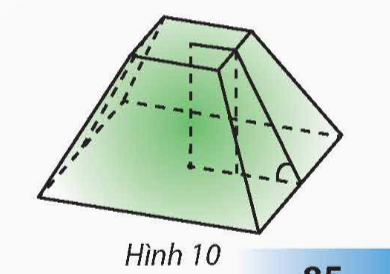
Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 135°. Tính số mét khối đất cần phải di chuyển ra khỏi hầm.
Bài 13 :
Cho chóp tứ giác \(S.ABCD\) có đáy là hình chữ nhật với \(AB = 4a,\) \(AD = 3a\). Các cạnh bên đều có độ dài \(5a\). Góc nhị diện \(\left[ {S,BC,A} \right]\) có số đo là
A. \({75^ \circ }46'\).
B. \({71^ \circ }21'\).
C. \({68^ \circ }31'\).
D. \({65^ \circ }12'\).
Bài 14 :
Trong không gian cho hai mặt phẳng \((\alpha), (\beta)\) cắt nhau theo giao tuyến d. Hai mặt phẳng \((\alpha), (\beta)\) tạo nên bao nhiêu góc nhị diện có cạnh của góc nhị diện là đường thẳng d?
Bài 15 :
Quan sát hình ảnh một quyển sổ được mở ra (Hình 35), mỗi trang sổ gợi nên hình ảnh của một nửa mặt phẳng. Nêu đặc điểm của hai nửa mặt phẳng đó.

Bài 16 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông và \(SA \bot \left( {ABCD} \right)\). Tính số đo theo đơn vị độ của góc nhị diện:
a) \(\left[ {B,SA,D} \right]\);
b) \(\left[ {B,SA,C} \right]\).
Bài 17 :
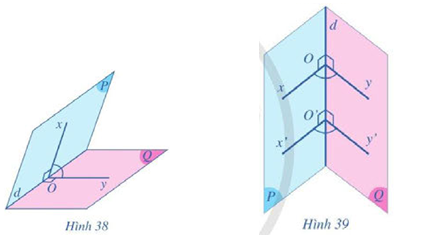
Cho góc nhị diện có hai mặt là hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cạnh của góc nhị diện là đường thẳng \(d\).
Qua một điểm \(O\) trên đường thẳng \(d\), ta kẻ hai tia \(Ox,Oy\) lần lượt thuộc hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cùng vuông góc với đường thẳng \(d\). Góc \(xOy\) gọi là góc phẳng nhị diện của góc nhị diện đã cho (Hình 38).
Giả sử góc \(x'Oy'\) cũng là góc phẳng nhị diện của góc nhị diện đã cho với \(O'\) khác \(O\) (Hình 39).
Hãy so sánh số đo của hai góc \(xOy\) và \(x'Oy'\).
Bài 18 :
\(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình thoi cạnh \(a\) và \(AC = a\).
a) Tính số đo của góc nhị diện \(\left[ {B,SA,C} \right]\).
b) Tính số đo của góc nhị diện \(\left[ {B,SA,D} \right]\).
c) Biết \(SA = a\), tính số đo của góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\).
Bài 19 :
Trong Hình 42, máy tính xách tay đang mở gợi nên hình ảnh của một góc nhị diện. Ta gọi số đo góc nhị diện đó là độ mở của màn hình máy tính. Tính độ mở của màn hình máy tính theo đơn vị độ, biết tam giác \(ABC\) có độ dài các cạnh là \(AB = AC = 30{\rm{ }}cm\) và \(BC = 30\sqrt 3 {\rm{ }}cm\).

Bài 20 :
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.
a) Tính côsin của góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\).
b) Tính côsin của số đo góc nhị diện \(\left[ {A',BD,C'} \right]\).
Bài 21 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a, biết \(\left( {SAB} \right) \bot \left( {ABCD} \right)\), \(\left( {SAD} \right) \bot \left( {ABCD} \right)\) và \(SA = a\). Tính côsin của số đo góc nhị diện \(\left[ {S,BD,C} \right]\) và góc nhị diện \(\left[ {B,SC,D} \right]\).
Bài 22 :
Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng \(\frac{{a\sqrt {15} }}{6}\). Tính số đo góc phẳng nhị diện \(\left[ {S,BC,A} \right]\).
Bài 23 :
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\). Tam giác ABC vuông tại A, \(\widehat {ABC} \) \( = {30^0}\), \(AC \) \( = a,SA \) \( = \frac{{a\sqrt 3 }}{2}\). Tính số đo góc phẳng nhị diện \(\left[ {S,BC,A} \right]\).
Bài 24 :
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\). Gọi \(I\) là hình chiếu của \(A\) trên đường thẳng \(BC\), \(\alpha \) là góc giữa đường thẳng \(SI\) và mặt phẳng \(\left( {ABC} \right)\), \(\beta \) là số đo của góc nhị diện \(\left[ {S,BC,A} \right]\). Phát biểu nào sau đây là đúng?
A. \(\alpha = {90^o} - \beta \)
B. \(\alpha = {180^o} - \beta \)
C. \(\alpha = {90^o} + \beta \)
D. \(\alpha = \beta \)
Bài 25 :
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), \(AB \bot BC\), \(SA = AB = 3a\), \(BC = 4a\). Gọi \(\alpha \), \(\beta \), \(\gamma \) lần lượt là số đo của các góc nhị diện \(\left[ {B,SA,C} \right]\), \(\left[ {A,BC,S} \right]\), \(\left[ {A,SC,B} \right]\). Tính
a) \(\cos \alpha \), \(\cos \beta \).
b*) \(\cos \gamma \).
Bài 26 :
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), \(ABCD\) là hình thoi cạnh \(a\), \(AC = a\), \(SA = \frac{a}{2}\). Tính số đo của góc nhị diện \(\left[ {S,CD,A} \right]\).
Bài 27 :
Cho hình chóp \(S.ABCD\) có \(AC\) cắt \(BD\) tại \(O\). Gọi \(\alpha \), \(\beta \) lần lượt là số đo của các góc nhị diện \(\left[ {A,SO,B} \right]\) và \(\left[ {B,SO,C} \right]\). Tính \(\alpha + \beta \).
Bài 28 :
Mệnh đề nào sau đây đúng?
-
A.
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({180^o}\)
-
B.
Số đo của góc nhị diện nhận giá trị từ \({90^o}\) đến \({180^o}\)
-
C.
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({90^o}\)
-
D.
Hai mặt phẳng cắt nhau tạo thành hai góc nhị diện
Bài 29 :
Kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều với chiều cao 98 m và cạnh đáy 180 m. Tính số đo góc nhị diện tạo bởi mặt bên và mặt đáy của kim tự tháp đó (đơn vị đo góc là độ, làm tròn đến hàng phần chục).
Bài 30 :
Một mái che giếng trời có dạng hình chóp tứ giác đều với độ dài cạnh đáy dài 2,4 m và độ dài các cạnh bên của hình chóp bằng 3 m . Gọi góc nhị diện giữa hai mặt bên đối diện của mái che giếng trời đó là \(\alpha \), tính \(\cos \alpha \) (làm tròn kết quả đến hàng phần trăm)?


















Danh sách bình luận