Tính giá trị của biểu thức: \(A = \frac{{{2^2}}}{{1.3}}.\frac{{{3^2}}}{{2.4}}.\frac{{{4^2}}}{{3.5}}.\frac{{{5^2}}}{{4.6}}\)
Triệt tiêu các thừa số giống nhau ở tử số và mẫu số
Ta có:
\(\begin{array}{l}A = \frac{{{2^2}}}{{1.3}}.\frac{{{3^2}}}{{2.4}}.\frac{{{4^2}}}{{3.5}}.\frac{{{5^2}}}{{4.6}}\\ = \frac{{2.2.3.3.4.4.5.5}}{{1.3.2.4.3.5.4.6}}\\ = \frac{{2.5}}{{1.6}}\\ = \frac{5}{3}\end{array}\)

Các bài tập cùng chuyên đề
Bài 1 :
Khi rút gọn phân số \(\frac{32}{40}\) ta được phân số tối giản là:
-
A.
\(\frac{-4}{5}\)
-
B.
\(\frac{4}{5}\)
-
C.
\(\frac{16}{20}\)
-
D.
\(\frac{16}{-20}\)
Bài 2 :
Rút gọn các phân số sau về phân số tối giản:
a) \(\frac{{ - 64}}{{96}}\)
b) \(\frac{{1414}}{{2626}}\)
c) \(\frac{{315 - 15}}{{530 - 30}}\)
Bài 3 :
Chia cả tử và mẫu của phân số \(\dfrac{{ - 28}}{{21}}\) cho 7 ta được phân số nào? Phân số vừa tìm được có bằng phân số \(\dfrac{{ - 28}}{{21}}\) không?
Bài 4 :
Trong các phân số \(\dfrac{{11}}{{23}};\dfrac{{ - 24}}{{15}}\), phân số nào là phân số tối giản? Nếu chưa là phân só tối giản, hãy rút gọn chúng.
Bài 5 :
Rút gọn các phân số sau :
\(\dfrac{{ - 12}}{{ - 4}}\);\(\dfrac{7}{{ - 35}}\); \(\dfrac{{ - 9}}{{27}}\)
Bài 6 :
Viết các số đo thời gian sau đây theo đơn vị giờ, dưới dạng phân số tối giản:
15 phút ; 90 phút
Bài 7 :
Trong các phân số \(\dfrac{{11}}{{23}};\dfrac{{ - 24}}{{15}}\), phân số nào là phân số tối giản? Nếu chưa là phân số tối giản, hãy rút gọn chúng.
Bài 8 :
Rút gọn các phân số sau:
\(\frac{{12}}{{ - 24}}\); \(\frac{{ - 39}}{{75}}\); \(\frac{{132}}{{ - 264}}\).
Bài 9 :
Dùng phân số có mẫu số dương nhỏ nhất để biểu thị xem số phút sau đây chiếm bao nhiêu phần của một giờ?
a) 15 phút;
b) 20 phút;
c) 45 phút;
d) 50 phút.
Bài 10 :
Dùng phân số để viết mỗi khối lượng sau theo tạ, theo tấn.
a) 20 kg;
b) 55 kg;
c) 87 kg
d) 91 kg.
Bài 11 :
Rút gọn các phân số \(\frac{{ - 18}}{{76}}\); \(\frac{{125}}{{ - 375}}\).
Bài 12 :
Viết phân số \(\frac{3}{{ - 5}}\) thành phân số có mẫu dương.
Bài 13 :
Rút gọn mỗi phân số sau về phân số tối giản:
\(\frac{14}{21}\); \(\frac{-36}{48}\); \(\frac{28}{-52}\); \(\frac{-54}{-90}\)
Bài 14 :
a) Rút gọn phân số \( \frac{-21}{39}\) về phân số tối giản
b) Viết các phân số bằng \( \frac{-21}{39}\) mà mẫu là số tự nhiên có hai chữ số
Bài 15 :
Biểu thị các số sau dưới dạng phân số tối giản với đơn vị là:
a) Mét: 15 cm; 40 mm
b) Mét vuông: 15 cm2; 35 dm2
Bài 16 :
Rút gọn các phân số sau:
\(\begin{array}{l}a)\frac{{{2^3}{{.3}^2}}}{{{2^2}{{.3}^3}}}\\b) - \frac{{{{2.3.5}^2}}}{{{3^2}{{.5}^3}}}\end{array}\)
Bài 17 :
Trong các phân số sau, phân số nào là phân số tối giản? Nếu chưa là phân số tối giản, hãy rút gọn.
\(\frac{{ - 30}}{{64}};\frac{{17}}{{29}};\frac{{10}}{{ - 25}}\)
Bài 18 :
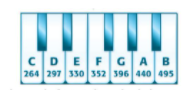
Tần số của các nốt nhạc tính theo đơn vị Hertz (Hz) được cho như sau:
Em hãy viết phân số thể hiện tỉ số giữa tần số nốt Đô (C) và nốt Mi (E), rồi rút gọn về phân số tối giản.
Bài 19 :
Viết số đo thời gian sau đây theo đơn vị giờ, dưới dạng phân số tối giản:
36 phút; 18 phút; 150 phút
Bài 20 :
Viết các số đo thời gian sau đây theo đơn vị giờ, dưới dạng phân số tối giản.
15 phút; 90 phút.
Bài 21 :
Viết các số đo độ dài sau đây theo đơn vị mét, dưới dạng phân số tối giản: 15 cm; 40 mm.
Bài 22 :
Một vòi nước chảy vào một bể không có nước, sau 40 phút thì đầy bể. Hỏi sau 10 phút, lượng nước đã chảy chiếm bao nhiêu phần bể?
Bài 23 :
Hà Linh tham gia một cuộc thi sáng tác và nhận được phần thưởng là số tiền 200 000 đồng. Hà Linh mua một món quà để tặng sinh nhật mẹ hết 80 000 đồng. Hỏi Hà Linh đã tiêu hết bao nhiêu phần số tiền mình được thưởng?
Bài 24 :
Rút gọn về phân số tối giản:
a) \(\frac{{ - 147}}{{252}}\)
b) \(\frac{{765}}{{900}}\)
c) \(\frac{{11.3 - 11.8}}{{17 - 6}}\)
d) \(\frac{{{3^5}{{.2}^4}}}{{{{8.3}^6}}}\)
e) \(\frac{{84.45}}{{49.54}}\)
Bài 25 :
Kết quả khi rút gọn phân số \(\frac{{20}}{{ - 140}}\) đến tối giản là:A. \( - \frac{{10}}{{70}}\).
B. \( - \frac{4}{{28}}\).
C. \( - \frac{2}{{14}}\).
D. \( - \frac{1}{7}\).


















Danh sách bình luận