Vé xem trận chung kết bóng đá Sea Game 30 được bán trực tiếp và bán qua mạng. Toàn bộ số vé bán qua mạng đã được bán hết trong 3 giờ, trong đó \(\frac{1}{3}\) số vé được bán hết trong giờ đầu tiên; giờ thứ hai bán được \(\frac{8}{{19}}\) tổng số vé bán được trong giờ thứ nhất và giờ thứ ba. Tính xem trong ba giờ bán vé qua mạng, giờ nào bán được ít vé nhất, giờ nào bán được nhiều vé nhất.
Bước 1: Giờ thứ hai bán được \(\frac{8}{{19}}\) tổng số vé bán được trong giờ thứ nhất và giờ thứ ba. Ta coi giờ thứ 2 bán được 8 phần thì tổng số vé bán được trong giờ thứ nhất và giờ thứ ba là 19 phần nên tổng số phần 3 giờ bán được là 8+ 19 = 27 phần. Do đó, giờ thứ 2 bán được \(\frac{8}{{27}}\) tổng số vé
Bước 2: Số vé còn lại sau 2 giờ bán là số vé bán trong giờ thứ 3
Bước 3: So sánh phân số chỉ số vé bán được mỗi giờ so trên tổng số vé. Phân số lớn nhất thì số vé bán được trong giờ đó là nhiều nhất
Vì giờ thứ hai bán được \(\frac{8}{{19}}\) tổng số vé bán được trong giờ thứ nhất và giờ thứ ba nên giờ thứ 2 bán được \(\frac{8}{{19 + 8}} = \frac{8}{{27}}\) tổng số vé
Giờ thứ ba bán được:
\(1 - \frac{1}{3} - \frac{8}{{27}} = \frac{{10}}{{27}}\) (tổng số vé)
Vì \(\frac{8}{{27}} < \frac{1}{3} < \frac{{10}}{{27}}\) nên giờ thứ 2 bán được ít vé nhất, giờ thứ 3 bán được nhiều vé nhất.

Các bài tập cùng chuyên đề
Bài 1 :
Sắp xếp các phân số \(\dfrac{{29}}{{40}};\dfrac{{28}}{{41}};\dfrac{{29}}{{41}}\) theo thứ tự tăng dần ta được
-
A.
\(\dfrac{{29}}{{41}};\dfrac{{28}}{{41}};\dfrac{{29}}{{40}}\)
-
B.
\(\dfrac{{29}}{{40}};\dfrac{{29}}{{41}};\dfrac{{28}}{{41}}\)
-
C.
\(\dfrac{{28}}{{41}};\dfrac{{29}}{{41}};\dfrac{{29}}{{40}}\)
-
D.
\(\dfrac{{28}}{{41}};\dfrac{{29}}{{40}};\dfrac{{29}}{{41}}\)
Bài 2 :
Sắp xếp các phân số \(\dfrac{7}{{11}};\dfrac{3}{{11}};\dfrac{{ - 7}}{5};0;\dfrac{{ - 4}}{5};\dfrac{9}{{11}}\) theo thứ tự tăng dần ta được:
-
A.
\(\dfrac{{ - 7}}{5} < \dfrac{{ - 4}}{5} < 0 < \dfrac{3}{{11}} < \dfrac{7}{{11}} < \dfrac{9}{{11}}\)
-
B.
\(\dfrac{{ - 7}}{5} < \dfrac{{ - 4}}{5} < 0 < \dfrac{7}{{11}} < \dfrac{9}{{11}} < \dfrac{3}{{11}}\)
-
C.
\(0<\dfrac{{ - 7}}{5} < \dfrac{{ - 4}}{5} < \dfrac{7}{{11}} < \dfrac{9}{{11}} < \dfrac{3}{{11}}\)
-
D.
\(0<\dfrac{9}{{11}} < \dfrac{3}{{11}}<\dfrac{{ - 7}}{5} < \dfrac{{ - 4}}{5} < \dfrac{7}{{11}}\)
Bài 3 :
So sánh hai phân số sau \({\rm{A}} = \frac{{{{10}^{2022}} + 1}}{{{{10}^{2023}} + 1}};{\rm{B}} = \frac{{{{10}^{2021}} + 1}}{{{{10}^{2022}} + 1}}\).
Bài 4 :
-
A.
\(\frac{2}{3} < \frac{3}{4}\)
-
B.
\(\frac{2}{3} > \frac{3}{4}\)
-
C.
\(\frac{2}{3} = \frac{3}{4}\)
-
D.
\(\frac{2}{3} \ge \frac{3}{4}\)
Bài 5 :
Tổ 1 gồm 8 bạn có tổng chiều cao là 115dm. Tổ 2 gồm 10 bạn có tổng chiều cao là 138dm. Hỏi chiều cao trung bình của các bạn ở tổ nào lớn hơn.
Bài 6 :
Cho \(a,\,b \in {\mathbb{N}^*}\). Hãy so sánh \(\frac{{a + n}}{{b + n}}\) và \(\frac{a}{b}\).
Bài 7 :
Cho \(a = \frac{{ - 3}}{7}\) và \(b = \frac{{ - 1}}{2}\). So sánh \(a\) và \(b\).
-
A.
\(a < b\);
-
B.
\(a = b\);
-
C.
\(a \ge b\)
-
D.
\(a > b\).
Bài 8 :
Tập hợp các số nguyên \(x\) thỏa mãn \(\frac{{ - 14}}{7} \le x < \frac{{16}}{8}\) là:
-
A.
\(\left\{ { - 2;\, - 1;\,0;\,1;\,2} \right\}\)
-
B.
\(\left\{ { - 1;\,0;\,1;\,2} \right\}\)
-
C.
\(\left\{ { - 2;\,-1;\,0;\,1} \right\}\)
-
D.
\(\left\{ { - 2;\, - 1;\,1} \right\}\)
Bài 9 :
Phân số bằng phân số \( \frac{-1}{5}\) là:
-
A.
\( \frac{-4}{20}\)
-
B.
\( \frac{-4}{-20}\)
-
C.
\( \frac{-5}{15}\)
-
D.
\( \frac{2}{10}\)
Bài 10 :
Cho \(A = \frac{1}{{1.2}} + \frac{1}{{2.3}} + ... + \frac{1}{{29.30}} + \frac{1}{{30.31}}\) và \(B = \frac{1}{{1.4}} + \frac{2}{{4.10}} + \frac{3}{{10.19}} + \frac{4}{{19.31}}\)
Chứng tỏ rằng \(A > B\).
Bài 11 :

Để giải quyết bài toán mở đầu, ta cần so sánh \(\dfrac{3}{4}\) và \(\dfrac{5}{6}\). Em hãy thực hiện các yêu
cầu sau:
• Viết hai phân số trên về hai phân số có cùng một mẫu dương bằng cách quy đồng mẫu số.
• So sánh hai phân số cùng mẫu vừa nhận được. Từ đó kết luận về phần bánh còn
lại của hai bạn Vuông và Tròn
Bài 12 :
So sánh các phân số sau:
a) \(\dfrac{7}{{10}}\) và \(\dfrac{{11}}{{15}}\)
b) \(\dfrac{{ - 1}}{8}\) và \(\dfrac{{ - 5}}{{24}}\)
Bài 13 :
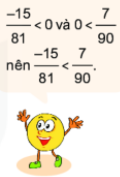
Không quy đồng mẫu số, em hãy so sánh \(\dfrac{{31}}{{32}}\) và \(\dfrac{{ - 5}}{{57}}\)
Bài 14 :
So sánh các phân số sau:
\(\dfrac{{ - 11}}{8}\) và \(\dfrac{1}{{24}}\)
Bài 15 :
So sánh các phân số sau:
\(\dfrac{3}{{20}}\) và \(\dfrac{6}{{15}}\)
Bài 16 :
Lớp 6A có \(\dfrac{4}{5}\) học sinh thích bóng bàn, \(\dfrac{7}{{10}}\) số học sinh thích bóng đá và \(\dfrac{1}{2}\) số học sinh thích bóng chuyền. Hỏi môn thể thao nào được các bạn học sinh lớp 6A yêu thích nhất?
Bài 17 :
a) Khối lượng nào lớn hơn: \(\dfrac{5}{3}kg\) hay \(\dfrac{{15}}{{11}}kg\)?
b) Vận tốc nào nhỏ hơn: \(\dfrac{5}{6}km/h\) hay \(\dfrac{4}{5}km/h\)?
Bài 18 :
Bảng sau cho biết chiều dài (theo đơn vị feet, 1 feet xấp xỉ bằng 30,48 cm) của một số loài động vật có vú nhỏ nhất trên thế giới.
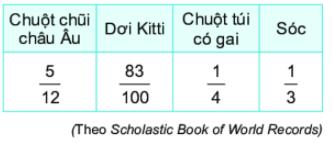
Hãy sắp xếp các động vật trên theo thứ tự chiều dài từ lớn đến bé.
Bài 19 :
Một bộ 5 chiếc cờ lê như hình bên có thể vặn được 5 loại ốc vít có các đường kính là:
\(\frac{9}{10}\) cm; \(\frac{4}{5}\) cm; \(\frac{3}{2}\) cm; \(\frac{6}{5}\) cm; \(\frac{1}{2}\) cm
Em hãy sắp xếp các số đo này theo thứ tự từ lớn đến bé
Bài 20 :
So sánh các phân số sau:
a) \(\dfrac{7}{{10}}\) và \(\dfrac{{11}}{{15}}\)
b) \(\dfrac{{ - 1}}{8}\) và \(\dfrac{{ - 5}}{{24}}\)
Bài 21 :

Không quy đồng mẫu số, em hãy so sánh \(\dfrac{{31}}{{32}}\) và \(\dfrac{{ - 5}}{{57}}\)
Bài 22 :
-
A.
\(–2,3; - \frac{6}{5}; - \frac{8}{9}; 0; \frac{9}{{14}}; 0,8\);
-
B.
\(0,8; - \frac{8}{9}; - \frac{6}{5}; 0; \frac{9}{{14}}; –2,3\);
-
C.
\(0,8; \frac{9}{{14}}; 0; - \frac{8}{9}; - \frac{6}{5}; –2,3\);
-
D.
\(0,8; \frac{9}{{14}}; 0; - \frac{6}{5}; –2,3; - \frac{8}{9}\).
Bài 23 :
So sánh hai phân số.
a) \(\frac{{ - 3}}{8}\) và \(\frac{{ - 5}}{{24}}\)
b) \(\frac{{ - 2}}{{ - 5}}\) và \(\frac{3}{{ - 5}}\)
c) \(\frac{{ - 3}}{{ - 10}}\) và \(\frac{{ - 7}}{{20}}\)
c) \(\frac{{ - 5}}{4}\) và \(\frac{{23}}{{ - 20}}\).
Bài 24 :
Tổ 1 gồm 8 bạn có tổng chiều cao là 115 dm. Tổ 2 gồm 10 bạn có tổng chiều cao là 138 dm. Hỏi chiều cao trung bình của các bạn ở tổ nào lớn hơn?
Bài 25 :
a) So sánh \(\frac{{ - 11}}{5}\) với \(\frac{{ - 7}}{4}\) bằng cách viết –2 ở dạng phân số có mẫu số thích hợp.
Từ đó suy ra kết quả so sánh \(\frac{{ - 11}}{5}\) với \(\frac{{ - 7}}{4}\).
b) So sánh \(\frac{{2020}}{{ - 2021}}\) với \(\frac{{ - 2022}}{{2021}}\).
Bài 26 :
Sắp xếp các số \(2;\,\frac{5}{{ - 6}}; \frac{3}{5};\, - 1;\,\frac{{ - 2}}{5};\,0\) theo thứ tự tăng dần.
Bài 27 :
Đưa hai phân số \(\frac{{ - 4}}{{ - 15}}\) và \(\frac{{ - 2}}{{ - 9}}\) về dạng hai phân số có mẫu dương rồi quy đồng mẫu của chúng.
Bài 28 :
So sánh \(\frac{{ - 7}}{{18}}\) và \(\frac{5}{{ - 12}}\)
Bài 29 :
Viết số nguyên dưới dạng phân số rồi so sánh.
a) \(\frac{{31}}{{15}}\) và 2;
b) \( - 3\) và \(\frac{7}{{ - 2}}\)
Bài 30 :
Thực hiện quy đồng mẫu số ba phân số \(\frac{{ - 2}}{5};\frac{{ - 3}}{8};\frac{3}{{ - 4}}\) rồi sắp xếp các phân số đó theo thứ tự tăng dần.


















Danh sách bình luận