Cho tam giác \(DEF\) có \(DE = 2\, cm\), \(EF=11\, cm\). Để tam giác \(DEF\) vuông tại \(D\) thì độ dài của cạnh \(DF\) là:
-
A.
\(7\, cm\);
-
B.
\(\sqrt{7}\, cm\);
-
C.
\(15\, cm\);
-
D.
\(\sqrt{15}\, cm\);
Nếu một tam giác có bình phương độ dài của một cạnh bằng tổng các bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.
Áp dụng định lí Pythagore đảo, để tam giác \(DEF\) vuông tại \(D\) thì:
\(D{E^2} + D{F^2} = E{F^2}\)
Suy ra \(D{F^2} = E{F^2} - D{E^2} = {\left( {\sqrt {11} } \right)^2} - {2^2} = 7\)
Suy ra \(DF = \sqrt 7 \,cm\)
Vậy để tam giác \(DEF\) vuông tại \(D\) thì độ dài của cạnh \(DF\) là \(\sqrt 7 \,cm\).
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
Lựa chọn phương án đúng nhất:
-
A.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác nhọn.
-
B.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
-
C.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác tù.
-
D.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác cân.
Bài 2 :
Tam giác ABC có AB = 3 cm, AC = 4cm, BC = 5cm. Tam giác ABC là tam giác gì?
-
A.
Tam giác nhọn
-
B.
Tam giác tù.
-
C.
Tam giác vuông.
-
D.
Không đủ dữ kiện để xác định
Bài 3 :
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
-
A.
15cm; 8cm; 18cm.
-
B.
21dm; 20dm; 29dm.
-
C.
5m; 6m; 8m.
-
D.
2m; 3m; 4m.
Bài 4 :
Cho tam giác ABC có \(\widehat B,\widehat C\) là các góc nhọn. Gọi H là chân đường vuông góc hạ từ A xuống BC. Biết AH = 6cm ; BH = 4,5cm và HC = 8cm. Khi đó tam giác ABC là tam giác gì?
-
A.
Tam giác cân
-
B.
Tam giác vuông
-
C.
Tam giác vuông cân
-
D.
Tam giác đều
Bài 5 :
Một tam giác có độ dài ba đường cao là 4,8cm ; 6cm ; 8cm. Tam giác đó là tam giác gì?
-
A.
Tam giác cân
-
B.
Tam giác vuông
-
C.
Tam giác vuông cân
-
D.
Tam giác đều
Bài 6 :
Đâu là độ dài 3 cạnh của một tam giác vuông:
-
A.
4cm, 7cm, 6cm.
-
B.
6cm, 10cm, 8cm.
-
C.
20cm, 12cm, 25cm.
-
D.
6cm, 11cm, 9cm.
Bài 7 :
Vẽ vào vở tam giác \(ABC\) có \(AB = 12\)cm, \(AC = 5\)cm, \(BC = 13\)cm, rồi xác định số đo \(\widehat {BAC}\) bằng thước đo góc.
Bài 8 :
Tìm tam giác vuông trong các tam giác sau:
a) Tam giác \(EFK\) có \(EF = 9\)m, \(FK = 12\)m, \(EK = 15\)m.
b) Tam giác \(PQR\) có \(PQ = 17\)cm, \(QR = 12\)cm, \(PR = 10\)cm.
c) Tam giác \(DEF\) có \(DE = 8\)m, \(DF = 6\)m, \(EF = 10\)m.
Bài 9 :
Chứng minh rằng tam giác \(ABC\) vuông trong các trường hợp sau:
a) \(AB = 8\)cm, \(AC = 15\)cm, \(BC = 17\)cm
b) \(AB = 29\)cm, \(AC = 21\)cm, \(BC = 20\)cm
c) \(AB = 12\)cm, \(AC = 37\), \(BC = 35\)cm
Bài 10 :
Thực hiện các hoạt động sau:
a) Vẽ một tam giác ABC có AB = 3 cm, AC = 4 cm và BC = 5 cm
b) Tính và so sánh diện tích của hình vuông có cạnh BC với tổng diện tích của hai hình vuông tương ứng có cạnh AB và AC.
c) Kiểm tra xem các góc A của tam giác ABC có phải là góc vuông hay không?
Bài 11 :
Tam giác có ba cạnh là 20 cm, 21 cm, 29 cm có phải là tam giác vuông hay không?
Bài 12 :
Tam giác có độ dài ba cạnh trong mỗi trường hợp sau có phải là tam giác vuông hay không?
a) 12 cm, 35 cm, 37 cm
b) 10 cm, 7 cm, 8 cm
c) 11 cm, 6 cm, 7 cm
Bài 13 :
Vẽ tam giác ABC có \(AB = 3cm,AC = 4cm,BC = 5cm.\)
a) So sánh \(B{C^2}\) và \(A{B^2} + A{C^2}.\)
b) Dùng thước đo góc để xác định số đo góc \(BAC.\)
Bài 14 :
Bạn Phát giải bài toán: “Tam giác ABC với \(AB = 5,AC = 13,BC = 12\) có phải là tam giác vuông hay không?” như sau:
Ta có:
\(A{B^2} + A{C^2} = {5^2} + {13^2} = 25 + 169 = 191;\)
\(B{C^2} = {12^2} = 144\)
Vì \(191 \ne 144\) nên \(A{B^2} + A{C^2} \ne B{C^2}\)
Vậy tam giác ABC không phải tam giác vuông.
Lời giải của Phát đúng hay sai? Vì sao?
Bài 15 :
Chứng minh tam giác EFG vuông trong các trường hợp sau:
a) \(FG = 12,EF = 35,EG = 37;\)
b) \(FG = 85,EF = 77,EG = 36;\)
c) \(FG = 12,EF = 13,EG = 5.\)
Bài 16 :
Tìm tam giác vuông trong các tam giác sau:
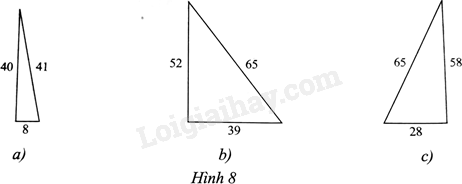
Bài 17 :
Ba số nào sau đây không thể là độ dài ba cạnh của một tam giác vuông?
A. 3; 4; 5.
B. 5; 12; 13.
C. 7; 24; 25.
D. 9; 40; 42.
Bài 18 :
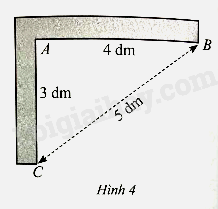
Hình 4 mô tả một chiếc thước của người thợ sử dụng khi xây móng nhà để kiểm tra xem hai phần móng nhà có vuông góc với nhau hay không . Trên hình, ta đo được \(AB = 4dm\), \(AC = 3dm\) và \(BC = 5dm\). Em hãy giải thích vì sao hai cạnh của chiếc thước đó vuông góc với nhau.
Bài 19 :
Những bộ ba số đo nào dưới đây là độ dài ba cạnh của một tam giác vuông
a) 1cm, 1cm, 2cm
b) 2cm, 4cm, 20cm
c) 5cm, 4cm, 3cm
d) 2cm, 2cm, \(2\sqrt 2 \)cm
Bài 20 :
Trong các bộ ba số đo dưới đây, đâu là số đo ba cạnh của một tam giác vuông?
A. 3 m; 5 m; 6 m
B. 6 m; 8 m; 10 m
C. 1 cm; 0,5 cm; 1,25 cm
D. 9 m; 16 m; 25 m.
Bài 21 :
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
-
A.
\(11\,cm;\,7\,cm;\,8\,cm\);
-
B.
\(12\,dm;\,15\,dm;\,18\,dm\);
-
C.
\(9\,m;\,12\,m;\,15\,m\);
-
D.
\(6\,cm;\,7\,cm;\,9\,cm\).
Bài 22 :
Cho tam giác \(ABC\) có độ dài ba cạnh \(AB = 6\,cm\), \(BC = 8\,cm\), \(AC = 10\,cm\). Khẳng định nào sau đây là đúng?
-
A.
Tam giác \(ABC\) vuông tại \(A\);
-
B.
Tam giác \(ABC\) vuông tại \(B\);
-
C.
Tam giác \(ABC\) vuông tại \(C\);
-
D.
Không thể kết luận được.
Bài 23 :
Xét các khẳng định sau:
I) Tam giác có độ dài ba cạnh là \(6\,cm,\,10\,cm,\,8\,cm\) là tam giác vuông.
II) Tam giác có độ dài ba cạnh là \(8\,cm,\,10\,cm,\,8\,cm\) không phải là tam giác vuông.
Chọn câu trả lời đúng.
-
A.
Chỉ có (I) đúng;
-
B.
Chỉ có (II) đúng;
-
C.
Cả (I) và (II) đều đúng;
-
D.
Cả (I) và (II) đều sai.
Bài 24 :
Cho các bộ ba số sau:
(a) \(1,\, cm,\, 2\, cm,\, 2\, cm\);
(b) \(2,\, cm,\, 4\, cm,\, 20\, cm\);
(c) \(5,\, cm,\, 4\, cm,\, 3\, cm\);
(d) \(2,\, cm,\, 2\, cm,\, 2\sqrt 2\, cm\).
Có bao nhiêu bộ ba số đo là độ dài ba cạnh của một tam giác vuông?
-
A.
0;
-
B.
1;
-
C.
2;
-
D.
3.
Bài 25 :
Một khung gỗ \(ABCD\) được tạo thành từ 5 thanh nẹp có độ dài như sau:
\(AB = CD = 48\, cm\)
\(BC = AD = 36\, cm\)
\(AC = 60\, cm\)
Kết luận nào sau đây là đúng?
-
A.
Tứ giác \(ABCD\) là hình bình hành;
-
B.
Tứ giác \(ABCD\) là hình thoi;
-
C.
Tứ giác \(ABCD\) là hình chữ nhật;
-
D.
Tứ giác \(ABCD\) là hình thang cân.
Bài 26 :
Một khung gỗ \(ABCD\) được tạo thành từ 5 thanh nẹp có độ dài như sau:
\(AB = CD = 48\, cm\)
\(BC = AD = 36\, cm\)
\(AC = 60\, cm\)
Kết luận nào sau đây là đúng?
-
A.
\(\widehat {ABC} + \widehat {ADC} = {90^o}\);
-
B.
\(\widehat {ABC} + \widehat {ADC} = {120^o}\)
-
C.
\(\widehat {ABC} + \widehat {ADC} = {150^o}\)
-
D.
\(\widehat {ABC} + \widehat {ADC} = {180^o}\)
Bài 27 :
Cho tam giác \(ABC\) có độ dài các cạnh \(AB\), \(BC\), \(CA\) lần lượt là \(4\,cm\), \(3\,cm\), \(5\,cm\). Trên tia đối của tia \(BA\) lấy điểm \(M\) sao cho \(BM = 2\,cm\), tại \(M\) kẻ đường thẳng vuông góc với \(AB\) cắt \(AC\) tại \(H\). Khẳng định nào sau đây là đúng?
-
A.
\(\widehat {CAB} + \widehat {CHM} = {180^o}\);
-
B.
\(\widehat {ABM} + \widehat {CHM} = {180^o}\);
-
C.
\(\widehat {BCH} + \widehat {CHM} = {180^o}\);
-
D.
\(\widehat {CAB} + \widehat {BAH} = {90^o}\);
Bài 28 :
Bộ ba số đo nào sau đây là độ dài ba cạnh của một tam giác vuông?
-
A.
3 cm, 4 cm, 6 cm.
-
B.
5 cm, 12 cm, 13 cm.
-
C.
4 cm, 5 cm, 6 cm.
-
D.
7 cm, 10 cm, 12 cm.
Bài 29 :
Tam giác có độ dài ba cạnh trong trường hợp nào sau đây là tam giác vuông?
-
A.
10cm, 6cm, 9cm.
-
B.
3cm, 4cm, 6cm.
-
C.
11cm, 6cm, 8cm.
-
D.
12cm, 35cm, 37cm.
Bài 30 :
Những bộ ba số đo nào dưới đây là độ dài ba cạnh của một tam giác vuông?
(1) 1cm, 1cm, 2cm
(2) \(1cm,{\rm{ }}1cm,{\rm{ }}\sqrt 2 cm\)
(3) 2cm, 4cm, 20cm
(4) \(2cm,{\rm{ }}4cm,{\rm{ }}\sqrt {20} cm\)
(5) 3cm, 4cm, 5cm
(6) 9cm, 16cm, 25cm


















Danh sách bình luận