Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của SC.
a) Tính khoảng cách từ S đến mặt phẳng (ABC).
b) Tính khoảng cách từ M đến mặt phẳng (SAG).
Sử dụng kiến thức về khoảng cách từ điểm đến mặt phẳng để tính: Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn thẳng MH được gọi là khoảng cách từ điểm M đến (P), kí hiệu d(M; (P)).
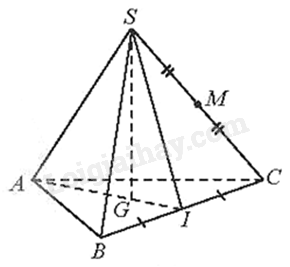
a) Vì S.ABC là hình chóp tam giác đều, G là trọng tâm của tam giác ABC nên \(SG \bot \left( {ABC} \right)\). Do đó, \(d\left( {S;\left( {ABC} \right)} \right) = SG\)
Vì tam giác ABC đều nên \(\widehat {ABC} = {60^0}\).
Gọi I là giao điểm của AG và BC. Khi đó, \(AG = \frac{2}{3}AI\)
Tam giác ABC đều nên AI là đường trung tuyến đồng thời là đường cao. Do đó, tam giác ABI vuông tại I. Suy ra: \(AI = AB.\sin \widehat {ABC} = \frac{{3a\sqrt 3 }}{2} \Rightarrow AG = a\sqrt 3 \)
Vì \(SG \bot \left( {ABC} \right),AG \subset \left( {ABC} \right) \Rightarrow SG \bot AG\)
Áp dụng định lí Pythagore vào tam giác ASG vuông tại G có:
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {a\sqrt 3 } \right)}^2}} = a\)
b) Vì \(SC \cap \left( {SAG} \right) = S \) \(\Rightarrow \frac{{d\left( {M,\left( {SAG} \right)} \right)}}{{d\left( {C,\left( {SAG} \right)} \right)}} = \frac{{MS}}{{CS}} = \frac{1}{2} \) \(\Rightarrow d\left( {M,\left( {SAG} \right)} \right) = \frac{1}{2}d\left( {C,\left( {SAG} \right)} \right)\)
Vì \(CB \bot AI,CB \bot SG \Rightarrow CB \bot \left( {SAG} \right)\). Mà \(CB \cap \left( {SAG} \right) = I\)
Do đó, \(d\left( {C,\left( {SAG} \right)} \right) = CI = \frac{1}{2}BC = \frac{{3a}}{2}\). Vậy \(d\left( {M,\left( {SAG} \right)} \right) = \frac{{3a}}{4}\)

Các bài tập cùng chuyên đề
Bài 1 :
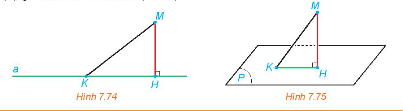
a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, vì sao MK ≥ MH (H.7.74)
b) Cho điểm M và mặt phẳng (P). Gọi H là hình chiếu của M trên (P). Với mỗi điểm K thuộc (P), giải thích vì sao MK ≥ MH (H.7.75).
Bài 2 :
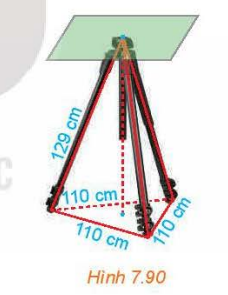
Giá đỡ ba chân ở Hình 7.90 đang được mở sao cho ba gốc chân cách đều nhau một khoảng cách bằng 110 cm. Tính chiều cao của giá đỡ, biết các chân của giá đỡ dài 129 cm.
Bài 3 :
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và \(OA = a,OB = a\sqrt 2 \) và \(OC = 2a\). Tính khoảng cách từ điểm \(O\) đến mặt phẳng \((ABC)\).
Bài 4 :
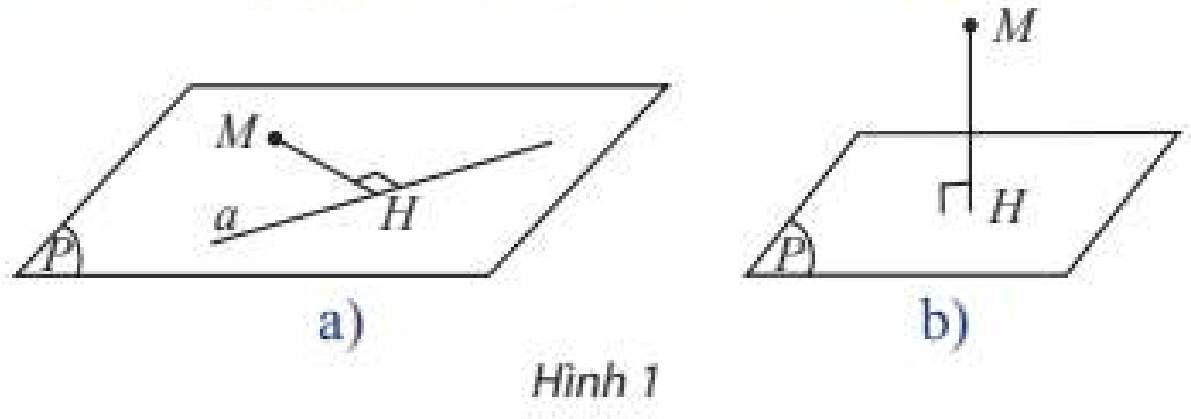
a) Cho điểm \(M\) và đường thẳng \(a\) không đi qua \(M\). Trong mặt phẳng \(\left( {M,a} \right)\), dùng êke để tìm điểm \(H\) trên \(a\) sao cho \(MH \bot a\) (Hình 1a). Đo độ dài đoạn \(MH\).
b) Cho điểm \(M\) không nằm trên mặt phẳng sàn nhà \(\left( P \right)\). Dùng dây dọi để tìm hình chiếu vuông góc \(H\) của \(M\) trên \(\left( P \right)\) (Hình 1b). Đo độ dài đoạn \(MH\).
Bài 5 :
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình thoi cạnh \(a\) có \(O\) là giao điểm của hai đường chéo, \(\widehat {ABC} = {60^ \circ },SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \). Tính khoảng cách từ \(O\) đến mặt phẳng \(\left( {SCD} \right)\).
Bài 6 :
Cho hình chóp tam giác đều \(S.ABC\) cạnh đáy bằng \(2a\) và chiều cao bằng \(a\sqrt 2 \). Khoảng cách từ tâm \(O\) của đáy \(ABC\) đến một mặt bên là
A. \(\frac{{a\sqrt {14} }}{7}\).
B. \(\frac{{a\sqrt 2 }}{7}\).
C. \(\frac{{a\sqrt {14} }}{2}\).
D. \(\frac{{2a\sqrt {14} }}{7}\).
Bài 7 :
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và \(SA \bot (ABC),SA = a\sqrt 2 \). Khoảng cách từ \(A\) đến mặt phẳng \((SBC)\) bằng
A. \(\frac{{6a}}{{11}}\).
B. \(\frac{{a\sqrt {66} }}{{11}}\).
C. \(\frac{{a\sqrt 6 }}{{11}}\).
D. \(\frac{{a\sqrt {11} }}{{11}}\).
Bài 8 :
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),AI \bot BC\left( {I \in BC} \right)\), \(AH \bot SI\left( {H \in SI} \right)\). Chứng minh rằng khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng \(AH\).
Bài 9 :
Khi lắp thiết bị cho nhà bạn Nam, bác thợ khoan tường tại vị trí \(M\) trên tường có độ cao so với nền nhà là \(MH = 80cm\). Quan sát Hình 61, nền nhà gợi nên mặt phẳng \(\left( P \right)\), cho biết độ dài đoạn thẳng \(MH\) gợi nên khái niệm gì trong hình học liên quan đến điểm \(M\) và mặt phẳng \(\left( P \right)\).
Bài 10 :
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a, gọi O là giao điểm của AC và BD. Khoản cách từ điểm O đến mặt phẳng (SBC) bằng
A. \(\frac{{a\sqrt 6 }}{6}\).
B. \(\frac{{a\sqrt 3 }}{3}\).
C. \(\frac{{a\sqrt 3 }}{2}\).
D. \(\frac{{a\sqrt 6 }}{3}\).
Bài 11 :
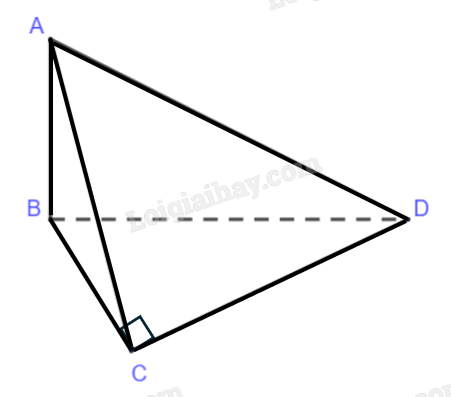
Cho tứ diện \(ABCD\) có cạnh \(AB\) vuông góc với mặt phẳng \(\left( {BCD} \right)\) và tam giác \(BCD\) vuông tại \(C\). Biết rằng \(AB = BC = 2a.\) Khoảng cách từ điểm \(B\) tới mặt phẳng \(\left( {ACD} \right)\) bằng bao nhiêu?
-
A.
\(\sqrt 2 a.\)
-
B.
\(\sqrt 3 a.\)
-
C.
\(a.\)
-
D.
\(\frac{{3a}}{2}.\)
Bài 12 :
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, biết \(SA = \frac{{a\sqrt 6 }}{2}\).
Bài 13 :
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A’BC) bằng
A. \(\frac{a}{{\sqrt 2 }}\)
B. \(\frac{{a\sqrt 6 }}{4}\)
C. \(\frac{{a\sqrt 3 }}{{\sqrt 7 }}\)
D. \(\frac{{a\sqrt 3 }}{4}\)
Bài 14 :
Cho hình chóp \(S.ABCD\) có mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt đáy \(\left( {ABCD} \right)\), tam giác \(SAB\) đều, đáy \(ABCD\) là hình vuông cạnh bằng \(a\). Gọi \(H\) là trung điểm của cạnh \(AB\). Khoảng cách từ điểm \(H\) đến mặt phẳng \(\left( {SAC} \right)\) bằng
A. \(\frac{{a\sqrt {30} }}{5}\).
B. \(\frac{{a\sqrt {21} }}{{14}}\).
C. \(\frac{{a\sqrt 6 }}{{10}}\).
D. \(\frac{{a\sqrt 6 }}{5}\).
Bài 15 :
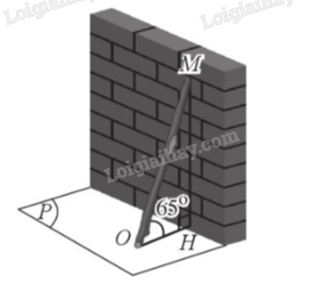
Hình dưới minh hoạ hình ảnh một chiếc gậy dài 3 m đặt dựa vào tường, góc nghiêng giữa chiếc gậy và mặt đất là \({65^o}\). Đầu trên của chiếc gậy đặt vào vị trí \(M\) của tường. Khoảng cách từ vị trí \(M\) đến mặt đất (làm tròn kết quả đến hàng phần mười của mét) bằng:
A. 2,7 m
B. 2,8 m
C. 2,9 m
D. 3,0 m
Bài 16 :
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thoi tâm O, SO vuông góc với mặt đáy. Biết cạnh hình thoi bằng 2024, góc BAD bằng \({120^o}\), khoảng cách từ điểm C đến mặt phẳng (SBD) bằng bao nhiêu?
Bài 17 :
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ A’ đến mặt phẳng (ABCD) bằng
-
A.
\(\frac{a}{2}\)
-
B.
\(a\)
-
C.
\(2a\)
-
D.
\(3a\)
Bài 18 :
Cho hình chóp S.ABCD có đáy hình vuông cạnh bằng I, SA vuông góc với mặt phẳng (ABCD) và \(SA = \frac{{\sqrt 3 }}{3}\). Khoảng cách từ điểm A đến mặt phẳng (SCD) bằng bao nhiêu (làm tròn kết quả đến hàng phần mười).
Bài 19 :
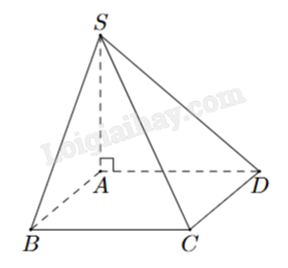
Kim tự tháp có hình dạng là một khối chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 230 m, độ dài cạnh bên bằng 214 m. Tính khoảng cách từ tâm của đáy đến mặt bên của kim tự tháp (kết quả làm tròn đến hàng đơn vị).
Bài 20 :
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a. SA = 2a vuông góc với mặt đáy (ABCD). Khoảng cách từ điểm B đến mặt phẳng (SAD) là
-
A.
\(a\)
-
B.
\(2a\)
-
C.
\(a\sqrt 3 \)
-
D.
\(\frac{a}{3}\)
Bài 21 :
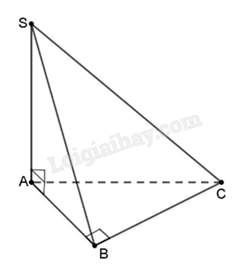
Cho hình chóp S.ABC, đáy là tam giác ABC vuông tại B, cạnh \(SA \bot (ABC)\). Chọn khẳng định đúng.
-
A.
\(d\left( {C,(SAB)} \right) = CS\)
-
B.
\(d\left( {A,(SBC)} \right) = AB\)
-
C.
\(d\left( {C,(SAB)} \right) = CB\)
-
D.
\(d\left( {S,(SBC)} \right) = SA\)
Bài 22 :
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(\sqrt 3 \). Gọi M, N và P lần lượt là trung điểm của các cạnh AB, AD và DC. Gọi H là giao điểm của CN và DM, biết SH vuông góc với (ABCD), SH = 3. Tính khoảng cách từ điểm C đến mặt phẳng (SBP).
Bài 23 :
Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(SA \bot (ABCD)\). Khẳng định nào sau đây sai?
-
A.
\(d\left( {S,(ABCD)} \right) = SA\)
-
B.
\(d\left( {D,(SAB)} \right) = DA\)
-
C.
\(d\left( {A,(SBC)} \right) = AB\)
-
D.
\(d\left( {D,(SAB)} \right) = d\left( {C,(SAB)} \right)\)
Bài 24 :
Cho hình chóp S.ABCD có đáy là tam giác vuông tại B có AB = a, \(BC = a\sqrt 3 \). Biết SA = 2a và \(SA \bot (ABC)\).
a) Tính khoảng cách từ A đến mặt phẳng (SBC).
b) Gọi M là trung điểm của AC. Tính khoảng cách từ A đến mặt phẳng (SBM).
Bài 25 :
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng \({45^o}\). Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC).
-
A.
\(d = \frac{{a\sqrt {1315} }}{{89}}\)
-
B.
\(d = \frac{{a\sqrt {1513} }}{{89}}\)
-
C.
\(d = \frac{{2a\sqrt {1315} }}{{89}}\)
-
D.
\(d = \frac{{2a\sqrt {1513} }}{{89}}\)
Bài 26 :
Kim tự tháp Kheops ở Ai Cập có dạng là hình chóp tứ giác đều có cạnh đáy dài 262 mét, cạnh bên dài 230 mét. Biết kho báu được đặt ở tâm của đáy kim tự tháp. Người ta xác định vị trí để đào con đường đến kho báu sao cho đoạn đường ngắn nhất. Tính độ dài đoạn đường ngắn nhất đó (kết quả làm tròn đến chữ số thập phân thứ nhất).
Bài 27 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, $\widehat{ABC} = 60^{o}$. Gọi O là giao điểm của AC và BD. Biết rằng $SO\bot(ABCD)$, $SO = \dfrac{3a}{4}$. Tính khoảng cách từ O đến mặt phẳng (SCD)?
Bài 28 :
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và $OA = a$, $OB = 2a$, $OC = 3a$. Tính khoảng cách từ điểm B đến mặt phẳng $(OAC)$.
-
A.
$a$.
-
B.
$a\sqrt{6}$.
-
C.
$3a$.
-
D.
$2a$.
Bài 29 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a, \(\widehat {ABC} = {60^o}\). Biết rằng \(SO \bot \left( {ABCD} \right)\), \(SO = \frac{{3a}}{2}\). Khoảng cách từ A đến mặt phẳng (SCD) bằng \(\frac{{m\sqrt {13} .a}}{n}\) với \(\frac{m}{n}\) là phân số tối giản, m > 0, n > 0. Giá trị m + n bằng bao nhiêu?



















Danh sách bình luận