Hình nón có đường sinh \(l\), chiều cao \(h\), bán kính đáy \(r.\) Phát biểu đúng là:
-
A.
\(l = r + h\).
-
B.
\({h^2} = {l^2} - {r^2}\).
-
C.
\(l = h\).
-
D.
\({h^2} = {l^2} + {r^2}\).
Sử dụng công thức liên hệ giữa độ dài đường sinh với bán kính đáy và chiều cao.
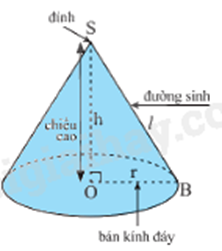
Ta có: \({l^2} = {r^2} + {h^2}\) suy ra \({h^2} = {l^2} - {r^2}\).
Đáp án B
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
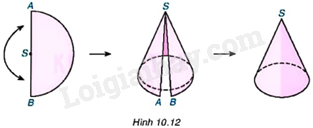
Cắt một nửa hình tròn bằng giấy cứng, đường kính \(AB = 20cm\)và tâm là S. Cuộn nửa hình tròn đó lại sao cho SA và SB sát vào nhau như Hình 10.12 (dùng băng keo dán), ta được một hình nón đỉnh S. Hãy cho biết độ dài đường sinh và chu vi đáy của hình nón đó.
Bài 2 :
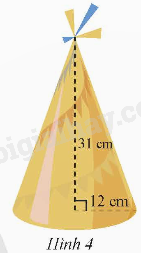
Chiếc mũ ở Hình 4 có dạng hình nón. Cho biết bán kính đáy, chiều cao và độ dài đường sinh của hình nón đó.
Bài 3 :
Hình nón có chiều cao 3 cm, bán kính đáy 4 cm, thì độ dài đường sinh là
A. 3 cm.
B. 4 cm.
C. 7 cm.
D. 5 cm.
Bài 4 :
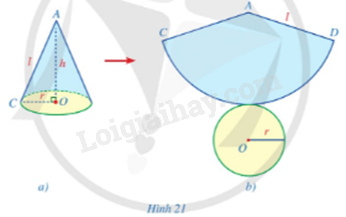
a) Chuẩn bị một hình nón bằng giấy có bán kính đáy là r, chiều cao là h và độ dài đường sinh là l (Hình 21a);
b) Từ hình nón đó, cắt rời đáy và cắt dọc theo đường sinh AC rồi trải phẳng ra, ta được hình khai triển mặt xung quanh của hình nón là một hình quạt tròn CAD tâm A với bán kính bằng độ dài đường sinh và độ dài cung CD bằng độ dài đường tròn đáy của hình nón (Hình 21b).
c) Tính diện tích hình quạt tròn CAD theo r và l.
Bài 5 :
Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Đẳng thức nào sau đây luôn đúng?
A. \({l^2} = {h^2} + {R^2}\).
B. \(\frac{1}{{{l^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{R^2}}}\).
C. \({R^2} = {h^2} + {l^2}\).
D. \({l^2} = hR\).
Bài 6 :
Cho hình nón có diện tích xung quanh \(25\pi \;c{m^2}\), bán kính đường tròn đáy bằng 5cm. Độ dài đường sinh của hình nón là
A. \(l = 1cm\).
B. \(l = \frac{5}{2}cm\).
C. \(l = 5cm\).
D. \(l = 3cm\).
Bài 7 :
Một hình quạt tròn có bán kính 29 cm, độ dài cung bằng \(42\pi \) cm. Người ta dùng hình quạt tròn này để tạo lập mặt xung quanh của một hình nón. Tính bán kính đáy và chiều cao của hình nón đó.
Bài 8 :
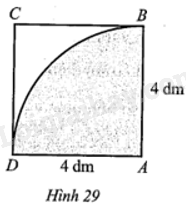
Từ một miếng tôn có dạng hình vuông ABCD cạnh 4 dm, người ta cắt ra một phần tư hình tròn tâm A bán kính AB = 4 dm (như phần được tô màu ở Hình 29) và cuộn lại thành một cái phễu hình nón. Tính chiều cao của cái phễu đó (theo đơn vị decimét và làm tròn kết quả đến hàng phần trăm).
Bài 9 :
Tam giác MNP vuông tại M có \(MN = 6cm,MP = 8cm\). Quay tam giác MNP quanh MN ta được hình nón có đường sinh bằng
A. 8cm.
B. 6cm.
C. 10cm.
D. 14cm.
Bài 10 :
Cho \(\Delta \)ABC vuông tại A có \(AB = 4cm,BC = 5cm\). Khi quay \(\Delta \)ABC quanh cạnh AC ta được một hình nón có chiều cao bằng:
A. 4cm.
B. 3cm.
C. 5cm.
D. 9cm.
Bài 11 :
Cho hình nón có diện tích xung quanh là $S_{xq}$ và bán kính đáy là $r$. Công thức nào dưới đây dùng để tính đường sinh $l$ của hình nón đã cho?
-
A.
$l = \frac{S_{xq}}{2\pi r}$.
-
B.
$l = \frac{2S_{xq}}{\pi r}$.
-
C.
$l = 2\pi S_{xq} r$.
-
D.
$l = \frac{S_{xq}}{\pi r}$.


















Danh sách bình luận