Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và các cạnh đều bằng a.
a) Chứng minh rằng \(SO \bot \left( {ABCD} \right)\).
b) Tính góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\).
c) Gọi \(M\) là trung điểm của cạnh \(SC\) và \(\alpha \) là góc giữa đường thẳng \(OM\) và mặt phẳng\(\left( {SBC} \right)\). Tính \({\rm{sin}}\alpha \).
a) Chứng minh \(SO\) vuông góc với hai đường thẳng cắt nhau nằm trên \(ABCD\) rồi suy ra \(SO \bot \left( {ABCD} \right)\).
b) Chứng minh \(AO \bot \left( {SBD} \right)\).
Tìm hình chiếu vuông góc của \(SA\) trên mặt phẳng \(\left( {SBD} \right)\), do đó góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\) bằng góc giữa hai đường thẳng \(SA\) và hình chiếu của nó.
c) Kẻ \(OK \bot BC\) tại \(K,OH \bot SK\) tại \(H\) thì ta chứng minh \(OH \bot \left( {SBC} \right)\),
Tìm hình chiếu vuông góc của \(OM\) trên mặt phẳng \(\left( {SBC} \right)\).
Góc giữa đường thẳng \(OM\) và mặt phẳng \(\left( {SBC} \right)\) bằng góc giữa hai đường thẳng \(OM\) và hình chiếu của nó.
Áp dụng tỉ số lượng giác cho tam giác vuông để tính góc.

a) Có SA = SB = SC = SD = AB = BC = CD = DA = a.
Vì O là trung điểm của AC và BD nên SO vừa là đường trung tuyến, vừa là đường cao của hai tam giác cân SAC và SBD.
Ta có: \(SO \bot AC\); \(SO \bot BD\) nên \(SO \bot \left( {ABCD} \right)\).
b) Vì \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AO\); mà \(AO \bot BD\) (hai đường chéo hình vuông) nên \(AO \bot \left( {SBD} \right)\).
Vì \(AO \bot \left( {SBD} \right)\) nên O là hình chiếu vuông góc của A trên mặt phẳng (SBD), do đó SO là hình chiếu vuông góc của SO trên mặt phẳng (SBD).
Góc giữa đường thẳng SA và mặt phẳng (SBD) bằng góc giữa hai đường thẳng SA và SO. Mà \(\left( {SA,SO} \right) = \widehat {ASO}\) nên góc giữa đường thẳng SA và mặt phẳng (SBD) bằng góc \(\widehat {ASO}\). Xét tam giác SAC có
Có \(\left\{ \begin{array}{l}S{A^2} + S{C^2} = {a^2} + {a^2} = 2{a^2}\\A{C^2} = A{B^2} + B{C^2} = {a^2} + {a^2} = 2{a^2}\end{array} \right. \Rightarrow S{A^2} + S{C^2} = A{C^2} \Rightarrow SA \bot SC\) (định lí Pythagore đảo), suy ra tam giác SAC vuông cân tại \(S\) và \(\widehat {ASO} = {45^o}\). Vậy góc giữa đường thẳng SA và mặt phẳng (SBD) bằng \({45^o}\).
c) Kẻ \(OK \bot BC\) tại K, \(OH \bot SK\) tại H.
Có \(\left\{ \begin{array}{l}SO \bot (ABCD) \Rightarrow SO \bot BC\\OK \bot BC\end{array} \right. \Rightarrow BC \bot (SOK) \Rightarrow BC \bot OH\).
Mà \(\left\{ \begin{array}{l}BC \bot OH\\SK \bot OH\end{array} \right. \Rightarrow OH \bot (SBC)\), hay H là hình chiếu của O trên mặt phẳng (SBC).
Suy ra HM là hình chiếu vuông góc của OM trên mặt phẳng (SBC), do đó góc giữa đường thẳng OM và mặt phẳng (SBC) bằng góc giữa hai đường thẳng OM và MH, mà \(\left( {OM,MH} \right) = \widehat {OMH}\) nên góc giữa đường thẳng OM và mặt phẳng (SBC) bằng góc \(\widehat {{\rm{OMH}}}\).
Vì tam giác SAC vuông cân tại S có đường cao SO nên OA = OC = SO.
Do đó, tam giác SOC vuông cân tại O, ta lại có OM = SM = MC = \(\frac{{SC}}{2} = \frac{a}{2}\).
\(OK = \frac{a}{2}\); \(SO = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\); \(SK = \sqrt {S{B^2} - B{K^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\).
Tam giác SOK vuông tại O, đường cao \({\rm{OH}}\) nên \({\rm{OH}}{\rm{.SK = SO}}{\rm{.OK}} \Leftrightarrow {\rm{OH}} = \frac{{{\rm{SO}} \cdot {\rm{OK}}}}{{SK}} = \frac{{a\sqrt 6 }}{6}\).
Vì tam giác OMH vuông tại H nên \({\rm{sin}}\alpha {\rm{\;}} = {\rm{sin}}\widehat {OMH} = \frac{{OH}}{{OM}} = \frac{{\sqrt 6 }}{3}\).

Các bài tập cùng chuyên đề
Bài 1 :
Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC) (H.7.36).
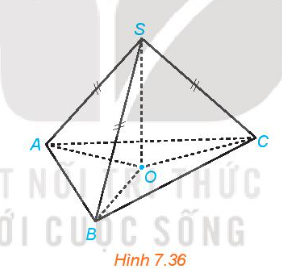
a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC.
b) Xác định hình chiếu của đường thẳng SA trên mặt phẳng (ABC).
c) Chứng minh rằng nếu \(AO \bot BC\) thì \(SA \bot BC.\)
d) Xác định hình chiếu của các tam giác SBC, SCA, SAB trên mặt phẳng (ABC)
Bài 2 :
Cho đường thẳng a và mặt phẳng (P) không vuông góc với nhau. Xét b là một đường thẳng nằm trong (P). Trên a, lấy hai điểm M, N tuỳ ý. Gọi M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) (H.7.34).

a) Hình chiếu của a trên mặt phẳng (P) là đường thẳng nào?
b) Nếu b vuông góc với M'N' thì b có vuông góc với a hay không?
c) Nếu b vuông góc với a thì b có vuông góc với M'N' hay không?
Bài 3 :
a) Nếu A là một điểm không thuộc mặt phẳng (P) và A’ là hình chiếu của A trên (P) thì đường thẳng AA’ có quan hệ gì với mặt phẳng (P)?
b) Nếu đường thẳng a vuông góc với mặt phẳng (P) thì hình chiếu của a trên (P) là gì?
Bài 4 :
Trên sân phẳng có một cây cột thẳng vuông góc với mặt sân.
a) Dưới ánh sáng mặt trời, bóng của cây cột trên sân có thể được nhìn như là hình chiếu của cây cột qua phép chiếu song song hay không?
b) Khi tia sáng mặt trời vuông góc với mặt sân, liệu ta có thể quan sát được bóng của cây cột trên sân hay không?
Bài 5 :
Cho hình chóp S.ABC có SA \( \bot \) (ABC), tam giác ABC vuông tại B.
a) Xác định hình chiếu của điểm S trên mặt phẳng (ABC).
b) Xác định hình chiếu của tam giác SBC trên mặt phẳng (ABC).
c) Xác định hình chiếu của tam giác SBC trên mặt phẳng (SAB).
Bài 6 :
Cho điểm S nằm ngoài mặt phẳng (P), có hình chiếu H trên (P). Với mỗi điểm M bất kì (không trùng H) trên mặt phẳng (P), ta gọi đoạn thẳng SM là đường xiên, đoạn thẳng HM là hình chiếu trên (P) của đường xiên đó. Chứng minh rằng:
a) Hai đường xiên SM và SM' bằng nhau khi và chỉ khi hai hình chiếu HM và HM' tương ứng của chúng bằng nhau.
b) Đường xiên SM lớn hơn đường xiên SM' nếu hình chiếu HM lớn hơn hình chiếu HM'.
Bài 7 :
Nếu cách tìm hình chiếu vuông góc của một đoạn thẳng \(AB\) trên trần nhà xuống nền nhà bằng hai dây dọi.
Bài 8 :
Cho đường thẳng \(a\) nằm trong mặt phẳng \(\left( P \right)\) và \(b\) là đường thẳng không thuộc \(\left( P \right)\) và không vuông góc với \(\left( P \right)\). Lấy hai điểm \(A,B\) trên \(b\) và gọi \(A',B'\) lần lượt là hình chiếu vuông góc của \(A\) và \(B\) trên \(\left( P \right)\).

a) Xác định hình chiếu \(b'\) của \(b\) trên \(\left( P \right)\).
b) Cho \(a\) vuông góc với \(b\), nêu nhận xét về vị trí tương đối giữa:
i) đường thẳng \(a\) và \(mp\left( {b,b'} \right)\);
ii) hai đường thẳng \(a\) và \(b'\).
c) Cho \(a\) vuông góc với \(b'\), nêu nhận xét về vị trí tương đối giữa:
i) đường thẳng \(a\) và \(mp\left( {b,b'} \right)\);
ii) giữa hai đường thẳng \(a\) và \(b\).
Bài 9 :
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\) và đáy \(ABCD\) là hình chữ nhật. Xác định hình chiếu vuông góc của điểm \(C\), đường thẳng \(CD\) và tam giác \(SC{\rm{D}}\) trên mặt phẳng \(\left( {SAB} \right)\).
Bài 10 :
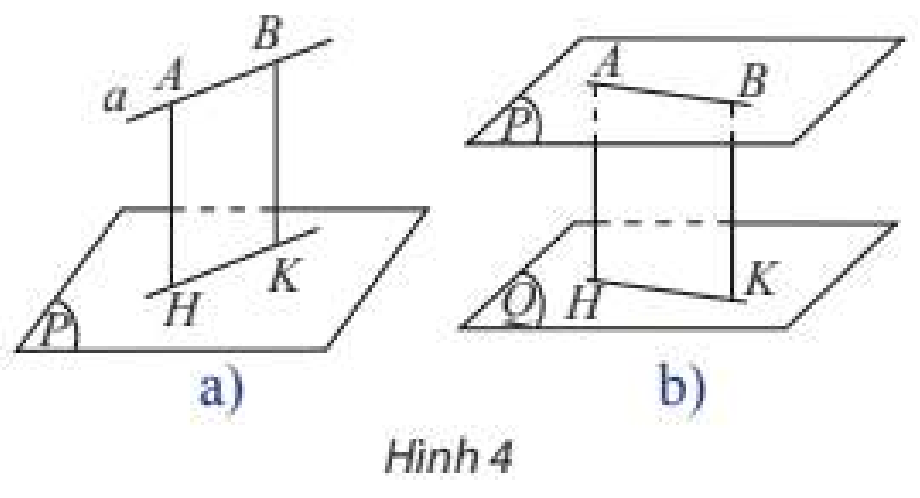
a) Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Lấy hai điểm \(A,B\) tuỳ ý trên \(a\) và gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(A\) và \(B\) trên \(\left( P \right)\) (Hình 4a). So sánh độ dài hai đoạn thẳng \(AH\) và \(BK\).
b) Cho hai mặt phẳng song song \(\left( P \right)\) và \(\left( Q \right)\). Lấy hai điểm \(A,B\) tuỳ ý trên \(\left( P \right)\) và gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(A\) và \(B\) trên \(\left( Q \right)\) (Hình 4b). So sánh độ dài hai đoạn thẳng \(AH\) và \(BK\).
Bài 11 :
Cho mặt phẳng (P) và đoạn thẳng AB. Xác định hình chiếu của đoạn thẳng AB trên mặt phẳng (P).
Bài 12 :
Trong Hình 27, mặt sàn gợi nên hình ảnh mặt phẳng (P), đường thẳng a không vuông góc với mặt phẳng (P), đường thẳng a’ là hình chiếu của đường thẳng a trên mặt phẳng (P), đường thẳng d nằm trong mặt phẳng (P). Quan sát Hình 27 và cho biết:
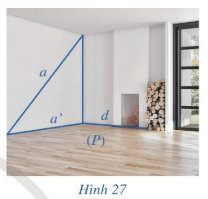
a) Nếu đường thẳng d vuông góc với hình chiếu a’ thì đường thẳng d có vuông góc với a hay không?
b) Ngược lại, nếu dường thẳng d vuông góc với a thì đường thẳng d có vuông góc với hình chiếu a’ hay không.
Bài 13 :
Một con diều được thả với dây căng, tạo với mặt đất một góc \({60^ \circ }\). Đoạn dây diều (từ đầu ở mặt đất đến đầu ở con diều) dài 10 m. Hỏi hình chiếu vuông góc trên mặt đất của con diều cách đầu dây diều trên mặt đất bao nhiêu centimét (lấy giá trị nguyên gần đúng)?
Bài 14 :
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right),{\rm{ }}AB \bot BC.\) Xét những phát biểu sau:
(1): AB là hình chiếu của SB trên (ABC);
(2): SB là hình chiếu của SC trên (SAB);
(3): AC là hình chiếu của SC trên (ABC). Số phát biểu đúng là:
A. 0.
B. 1.
C. 2.
D. 3.
Bài 15 :
Cho mặt phẳng (P) và hai điểm A, B sao cho B thuộc (P) và 4 không thuộc (P). Điểm C chuyển động trên mặt phẳng (P) thoả mãn \(\widehat {ACB} = {90^0}.\) Chứng minh rằng C chuyển động trên một đường tròn cố định trong (P).
Bài 16 :
Cho hình chóp.S ABCD có đáy là hình vuông cạnh a, cạnh SA vuông góc với mặt phẳng (ABCD). Hình chiếu vuông góc của DSCD lên mặt phẳng (ABCD) là
-
A.
\(\Delta ABC\)
-
B.
\(\Delta ACD\)
-
C.
\(\Delta SAD\)
-
D.
\(\Delta SBA\)


















Danh sách bình luận