Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^o}\) nội tiếp đường tròn \(\left( {O;\,\,3\,{\rm{cm}}} \right)\). Khi đó diện tích tam giác \(ABC\) là
-
A.
\(\frac{{9\sqrt 3 }}{4}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
-
B.
\(\frac{{3\sqrt 3 }}{2}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
-
C.
\({\rm{3}}\sqrt 3 \,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
-
D.
\(\frac{{3\sqrt 3 }}{4}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Kẻ \(AH \bot BC\), khi đó AH là đường trung trực của BC và là phân giác của góc BAC nên suy ra tam giác AOC đều, ta tính được HC và HA theo R.
Từ đó sử dụng công thức tính diện tích tam giác để tính diện tích tam giác ABC.
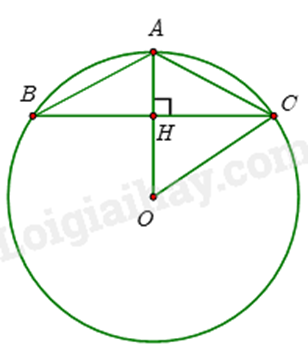
Kẻ \(AH \bot BC\).
Khi đó \(AH\) là đường trung trực của \(BC\) (vì tam giác ABC cân tại A) nên \(AH\) đi qua \(O\) (tính đối xứng của đường tròn).
AH đồng thời là đường phân giác của góc BAC, do đó \(\widehat {HAC} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.120^\circ = 60^\circ \).
Vì tam giác AOC có OA = OC và \(\widehat {OAC} = 60^\circ \) nên \(\Delta AOC\) đều, do đó \(HC = \frac{{R\sqrt 3 }}{2}\) và \(HA = \frac{R}{2}\).
Vì vậy
\(\begin{array}{l}{S_{ABC}} = \frac{1}{2}BC.AH = HC.HA = \frac{{R\sqrt 3 }}{2}.\frac{R}{2}\\ = \frac{{{R^2}\sqrt 3 }}{4} = \frac{{{3^2}\sqrt 3 }}{4} = \frac{{9\sqrt 3 }}{4}\,({\rm{c}}{{\rm{m}}^{\rm{2}}})\end{array}\)
Đáp án A
Đáp án : A

Các bài tập cùng chuyên đề
Bài 1 :
Cho tam giác \(ABC\) nội tiếp đường tròn tâm \(O.\) Gọi $P,\,Q,R$ lần lượt là giao điểm của các tia phân giác trong góc \(A,\,B,\,C\) với đường tròn. Giả sử rằng AP cắt RQ tại S. Khi đó:
-
A.
\(\widehat {ASQ} = {30^0}\)
-
B.
\(\widehat {ASQ} = {45^0}\)
-
C.
\(\widehat {ASQ} = {60^0}\)
-
D.
\(\widehat {ASQ} = {90^0}\)
Bài 2 :
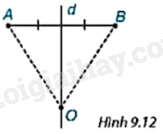
Cho d là đường trung trực của đoạn thẳng AB và O là một điểm trên d (H.9.12). Hỏi đường tròn tâm O đi qua điểm A thì có đi qua điểm B không?
Bài 3 :
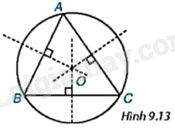
Cho tam giác ABC có ba đường trung trực đồng quy tại O (H.9.13). Hãy giải thích tại sao đường tròn (O; OA) đi qua ba đỉnh của tam giác ABC.
Bài 4 :
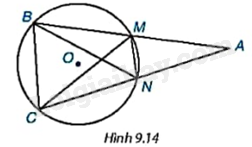
Hãy kể tên bốn tam giác nội tiếp đường tròn (O) trong Hình 9.14.
Bài 5 :
Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng \(\widehat {BAH} = \widehat {OAC}\).
Bài 6 :
Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm của đường trung trực của đoạn thẳng AB và BC (Hình 1).

a) So sánh độ dài của đoạn thẳng OA, OB và OC.
b) Vẽ đường tròn đi qua ba điểm A, B, C.
Bài 7 :
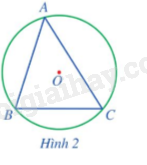
Cho biết các đỉnh của tam giác ABC (Hình 2) có thuộc đường tròn (O) hay không?
Bài 8 :
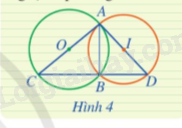
Quan sát Hình 4 và cho biết trong hai đường tròn (O) và (I), đường tròn nào ngoại tiếp tam giác ABC, đường tròn nào ngoại tiếp tam giác ABD?
Bài 9 :
Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O) đường kính AD = 2R. Gọi M là trung điểm của cạnh BC và H là trực tâm của tam giác ABC. Chứng minh:
a) \(BD \bot AB,CD \bot AC.\)
b) Tứ giác BHCD là hình bình hành.
c) \(A{C^2} + B{H^2} = 4{R^2}.\)
d) Ba điểm H, M, D thẳng hàng và AH = 2OM.
Bài 10 :
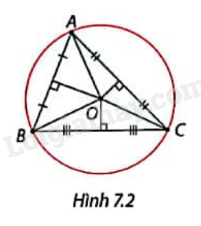
Vẽ tam giác ABC. Vẽ ba đường trung trực của tam giác ABC và xác định giao điểm O của chúng. Giải thích vì sao đường tròn tâm O bán kính OA đi qua cả ba đỉnh của \(\Delta \)ABC. (Hình 7.2)
Bài 11 :
Cho tam giác nhọn ABC nội tiếp đường tròn (O), AD là đường kính của (O) và H là trực tâm của \(\Delta \)ABC. Chứng minh BHCD là hình bình hành.
Bài 12 :
\(\Delta ABC\) nội tiếp đường tròn \(\left( O \right)\). Biết rằng \(\widehat {BOC} = 120^\circ \), \(\widehat {BAC}\) có số đo bằng
-
A.
\(40^\circ \).
-
B.
\(60^\circ \).
-
C.
\(20^\circ \).
-
D.
\(75^\circ \).
Bài 13 :
Cho tam giác \(ABC\) nhọn, nội tiếp trong đường tròn \(\left( {O;R} \right)\). H là trực tâm của tam giác \(ABC\). Vẽ \(OK \bot BC\,\,\left( {K \in BC} \right)\). Tỉ số \(\frac{{OK}}{{AH}}\) là:
-
A.
2.
-
B.
1.
-
C.
\(\frac{1}{2}\).
-
D.
\(\frac{1}{4}\).
Bài 14 :
Cho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right)\)đường kính \(AD = 2R\). Gọi \(M\) là trung điểm của cạnh \(BC\), H là trực tâm của \(\Delta ABC\).
a) \(DB \bot AB\).
b) Tứ giác \(BHCD\) là hình chữ nhật.
c) \(A{C^2} + B{H^2} = 4{R^2}\).
d) \(AH = 2OM\).
Bài 15 :
Cho tam giác \(ABC\)\(\left( {AC < BC} \right)\) nội tiếp đường tròn \(\left( O \right)\) có \(AB\) là đường kính. Từ tâm \(O\) vẽ đường thẳng song song với \(AC\)và cắt \(\left( O \right)\) tại điểm \(I\) (\(I\) thuộc cung nhỏ $\overset\frown{BC}$). Vẽ tiếp tuyến của đường tròn \(\left( O \right)\) tại \(B\) và cắt đường thẳng \(OI\) tại \(M\).
a) \(OI \bot BC\).
b) \(CM\) là tiếp tuyến của đường tròn \(\left( O \right)\).
c) Đường tròn ngoại tiếp \(\Delta OBM\) không đi qua C.
d) Tứ giác \(OBMC\) là hình vuông khi \(\Delta ABC\) vuông cân.
Bài 16 :
Vẽ đường tròn (O) ngoại tiếp tam giác MNP trong các trường hợp sau:
a) \(\widehat M,\widehat N,\widehat P\) đều nhọn;
b) \(\widehat M = {90^o}\)
c) \(\widehat M > {90^o}\)
Bài 17 :
Cho tam giác nhọn ABC (\(\widehat B > \widehat C\)), phân giác AM. Gọi O, O1, O2 lần lượt là tâm đường tròn ngoại tiếp các tam giác ABC, AMB, AMC. Chứng minh rằng:
a) OO1, OO2, O1O2 lần lượt là các đường trung trực của AB, AC, AM;
b) Tam giác OO1O2 cân.
Bài 18 :
Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng \(\widehat {ACB} = {50^o},\widehat {ABC} = {70^o}\), tính số đo các cung nhỏ $\overset\frown{BC},\overset\frown{CA},\overset\frown{AB}$ của đường tròn (O).
Bài 19 :
Cho tam giác ABC cân tại A và nội tiếp đường tròn (O). Tính số đo các góc của tam giác ABC, biết rằng \(\widehat {BOC} = {100^o}\).
Bài 20 :
Cho tam giác ABC có trực tâm H và nội tiếp đường tròn (O). Chứng minh rằng:
a) \(\widehat {OBC} = {90^o} - \widehat {BAC}\);
b) \(\widehat {BAH} = \widehat {OAC}\).
Bài 21 :
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Cho điểm M trên cạnh BC của tam giác ABC và điểm D trên cung nhỏ BC của (O) sao cho \(\widehat {BAD} = \widehat {MAC}\). Chứng minh rằng $\Delta AMB\backsim \Delta ACD$.
Bài 22 :
Cho tam giác ABC có đường cao AH (H\( \in \)BC) và nội tiếp đường tròn (O). Vẽ đường kính AD của đường tròn (O). Chứng minh AB.AC = AH.AD
Bài 23 :
Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng \(\widehat {BAH} = \widehat {OAC}\).
Bài 24 :
Cho tam giác ABC nội tiếp đường tròn (O). Trên các cạnh AB, AC lần lượt lấy các điểm M và N (M khác A và B, N khác A và C). Giả sử đường tròn ngoại tiếp tam giác AMN cắt đường tròn (O) tại một điểm S khác A. Chứng minh rằng \(\frac{{SM}}{{SB}} = \frac{{SN}}{{SC}}\).
Bài 25 :
Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng \(\widehat {BOC} = {120^o}\) và \(\widehat {OCA} = {20^o}\). Tính số đo các góc của tam giác ABC.
Bài 26 :
Cho tam giác ABC nhọn có trực tâm H và nội tiếp đường tròn (O). Lấy D là điểm đối xứng với A qua O. Chứng minh rằng DH đi qua trung điểm BC.
Bài 27 :
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC và M là trung điểm của BC. Chứng minh rằng \(AH = 2OM\).
Bài 28 :
Trong các đường tròn dưới đây, đường tròn nào là đường tròn ngoại tiếp tam giác ABC.
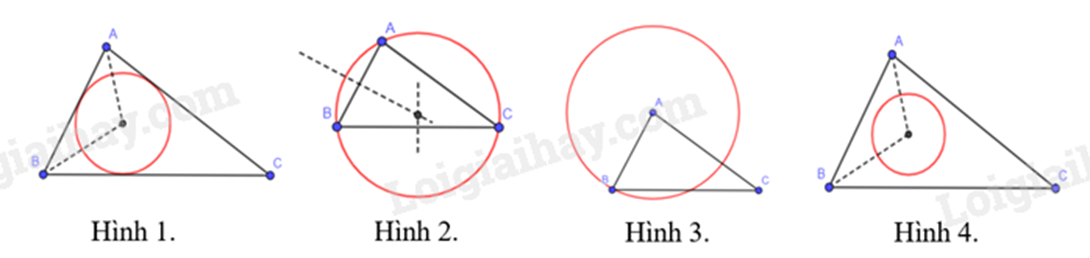
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.


















Danh sách bình luận