Thời gian (phút) truy cập internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Tìm trung vị của mẫu số liệu ghép nhóm trên (kết quả viết dưới dạng số thập phân).
Đáp án:
Đáp án:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.({u_{m + 1}} - {u_m})\).
Cỡ mẫu: n = 3 + 12 + 15 + 24 + 2 = 56.
Gọi \({x_1};{x_2};...;{x_{33}}\) là thời gian học sinh truy cập internet sắp xếp theo thứ tự không giảm.
Có \(\frac{n}{2} = \frac{{56}}{2} = 28\) nên \({Q_2} = \frac{{{x_{28}} + {x_{29}}}}{2} \in [15,5;18,5)\).
\({Q_2} = 15,5 + \frac{{\frac{{56}}{2} - (3 + 12)}}{{15}}.(18,5 - 15,5) = 18,1\).

Các bài tập cùng chuyên đề
Bài 1 :
Trong tuẫn lễ bảo vệ môi trường, các học sinh khối 11 tiến hành thu nhặt vỏ chai nhựa để tái chế. Nhà trường thống kê kết quả thu nhặt vỏ chai của học sinh khối 11 ở bảng sau:
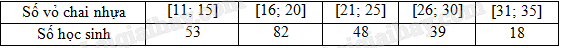
Hãy tìm trung vị của mẫu số liệu ghép nhóm trên.
-
A.
\(19,27\)
-
B.
\(19,59\)
-
C.
\(20,2\)
-
D.
\(18,6\)
Bài 2 :
Trong tuẫn lễ bảo vệ môi trường, các học sinh khối 11 tiến hành thu nhặt vỏ chai nhựa để tái chế. Nhà trường thống kê kết quả thu nhặt vỏ chai của học sinh khối 11 ở bảng sau:
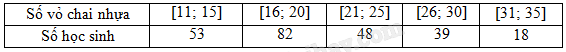
Hãy tìm trung vị của mẫu số liệu ghép nhóm trên.
-
A.
19,51.
-
B.
19,59.
-
C.
20,2.
-
D.
18,6.
Bài 3 :
Ghi lại tốc độ bóng trong 200 lần giao bóng của một vận động viên môn quần vợt cho kết quả như bảng bên.
|
Tốc độ v (km/h) |
Số lần |
|
\(150 \le v < 155\) |
\(18\) |
|
\(155 \le v < 160\) |
\(28\) |
|
\(160 \le v < 165\) |
\(35\) |
|
\(165 \le v < 170\) |
\(43\) |
|
\(170 \le v < 175\) |
\(41\) |
|
\(175 \le v < 180\) |
\(35\) |
Tính trung vị của mẫu số liệu ghép nhóm này.
Bài 4 :
Cho mẫu số liệu ghép nhóm về chiều cao của 21 cây na giống
Gọi \({X_1},\;{X_2},\; \ldots ,\;{X_{21}}\) là chiều cao của các cây giống, đã được sắp xếp theo thứ tự tăng dần. Khi đó, \({X_1},\;\;...,{X_3}\) thuộc \(\left[ {0;5} \right),\;{X_4},\; \ldots ,{X_{11}}\) thuộc \(\left[ {5;10} \right), \ldots \) Hỏi trung vị thuộc nhóm nào?
Bài 5 :
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
|
Thời gian (phút) |
[0;20) |
[20; 40) |
[40; 60) |
[60; 80) |
[80; 100) |
|
Số học sinh |
5 |
9 |
12 |
10 |
6 |
Nhóm chứa trung vị là
A. \(\left[ {0;200} \right)\)
B. \(\left[ {20;40} \right)\)
C. \(\left[ {40;60} \right)\)
D. \(\left[ {60;80} \right)\)
Bài 6 :
Trong một hội thao, thời gian chạy 200 m của một nhóm các vận động viên được ghi lại ở bảng sau:

Dựa vào bảng số liệu trên, ban tổ chức muốn chọn ra khoảng 50% số vận động viên chạy nhanh nhất để tiếp tục thi vòng 2. Ban tổ chức nên chọn các vận động viên có thời gian chạy không quá bao nhiêu giây?
Bài 7 :
Hãy trả lời câu hỏi ở Hoạt động mở đầu.
Bài 8 :
Trung vị của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A. \(\begin{array}{*{20}{c}}{\left[ {7;9} \right)}\end{array}\).
B. \(\begin{array}{*{20}{c}}{\left[ {9;11} \right)}\end{array}\).
C. \(\begin{array}{*{20}{c}}{\left[ {11;13} \right)}\end{array}\).
D. \(\begin{array}{*{20}{c}}{\left[ {13;15} \right)}\end{array}\).
Bài 9 :
Cho mẫu số liệu về thời gian (phút) đi từ nhà đến trường của một số học sinh như sau:

Tính trung vị của mẫu số liệu trên.
Bài 10 :
Trong một hội thao, thời gian chạy 200 m của một nhóm vận động viên được ghi lại trong bảng sau:

Dựa vào bảng dữ liệu trên, ban tổ chức muốn chọn ra khoảng 50% số vận động viên chạy nhanh nhất để tiếp tục thi vòng 2. Ban tổ chức nên chọn các vận động viên có thời gian chạy không quá bao nhiêu giây (kết quả làm tròn đến hàng phần mười)?
Bài 11 :
Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận đấu bóng đá tại giải ngoại hạng Anh được cho trong bảng thống sau:

Tìm trung vị của mẫu số liệu này và giải thích ý nghĩa của giá trị thu được.
Bài 12 :
Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau:

Nhóm chứa trung vị của mẫu số liệu là
A. \(\left[ {2;3,5} \right)\)
B. \(\left[ {3,5;\,\,5} \right)\)
C. \(\left[ {5;\,\,6,5} \right)\)
D. \(\left[ {6,5;\,\,8} \right)\)
Bài 13 :
Bạn Chi vào website của một cửa hàng bán điện thoại tìm hiểu và đã thống kê số lượng một loại điện thoại theo giá bán cho kết quả như sau:

a) Đọc và giải thích mẫu số liệu ghép nhóm này.
b) 50% loại điện thoại trên có giá dưới bao nhiêu?
Bài 14 :
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Trung vị của mẫu số liệu ghép nhóm trên là
A. 157,76.
B. 157,25.
C. 158,25.
D. 160,45.
Bài 15 :
Xác định trung vị của mẫu số liệu ghép nhóm ở bảng 1.
Bài 16 :
Trong phòng thí nghiệm, người ta chia 99 mẫu vật thành năm nhóm căn cứ trên khối lượng của chúng (đơn vị: gam) và lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy như Bảng 10.
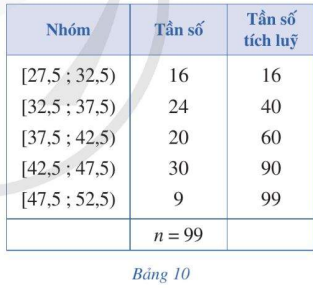
a) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng: \(\frac{n}{2} = \frac{{99}}{2} = 49,5\) có đúng không?
b) Tìm đầu mút trái \(r\), độ dài \(d\), tần số \({n_3}\) của nhóm 3; tần số tích lũy \(c{f_2}\) của nhóm 2.
c) Tính giá trị \({M_e}\) theo công thức sau: \({M_e} = r + \left( {\frac{{49,5 - c{f_2}}}{{{n_3}}}} \right).d\)
Bài 17 :
Người ta tiến hành phỏng vấn 40 người về một mẫu áo khoác. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm là 100. Kết quả được trình bày trong bảng ghép nhóm sau:
|
Nhóm |
[50;60) |
[60;70) |
[70;80) |
[80;90) |
[90;100) |
|
|
Tần số |
4 |
5 |
23 |
6 |
2 |
N = 40 |
Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị
-
A.
74.
-
B.
75.
-
C.
76.
-
D.
77.
Bài 18 :
Cho mẫu số liệu ghép nhóm về thu thập của các công nhân tại một doanh nghiệp lớn:

Nhóm chứa trung vị là
A. \([5;10)\).
B. \([10;15)\).
C. \([15;20)\).
D. \([20;25)\).
Bài 19 :
Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Nhóm chứa trung vị của mẫu số liệu trên là
-
A.
[40;60)
-
B.
[20;40)
-
C.
[60;80)
-
D.
[80;100)
Bài 20 :
Thống kê chiều cao các cây bạch đàn trong vườn ươm của một lâm trường theo bảng số liệu sau:

Trung vị của mẫu số liệu là:
-
A.
100
-
B.
102
-
C.
105
-
D.
110
Bài 21 :
Trong tuẫn lễ bảo vệ môi trường, các học sinh khối 12 tiến hành thu nhặt vỏ chai nhựa để tái chế. Nhà trường thống kê kết quả thu nhặt vỏ chai của học sinh khối 12 ở bảng sau:

Hãy tìm trung vị của mẫu số liệu ghép nhóm trên.
-
A.
19,51
-
B.
19,59
-
C.
20,1
-
D.
18,3
Bài 22 :
Giáo viên chủ nhiệm khảo sát thời gian sử dụng Internet trong một ngày của 50 học sinh thành 7 nhóm (đơn vị: phút) và lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy như sau:
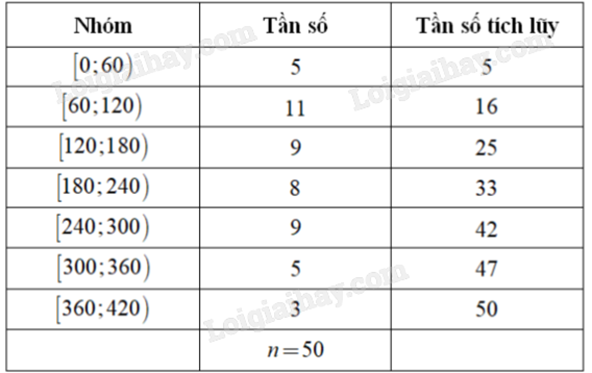
Trung vị của mẫu số liệu bằng
-
A.
175
-
B.
180
-
C.
186
-
D.
187
Bài 23 :
Cho mẫu số liệu ghép nhóm của chiều cao của cây cao su trong một nông trường:

Trung vị của mẫu số liệu trên là
-
A.
\(\frac{{1121}}{{60}}\)
-
B.
\(\frac{{75}}{4}\)
-
C.
\(\frac{{1127}}{{60}}\)
-
D.
\(\frac{{1123}}{{60}}\)
Bài 24 :
Khảo sát thời gian tập thể dục của một số học sinh thu được mẫu số liệu ghép nhóm như sau:

Tìm trung vị của mẫu số liệu trên (kết quả làm tròn đến hàng phần mười).
-
A.
32,2.
-
B.
33,2.
-
C.
32,1.
-
D.
33,1.
Bài 25 :
Bảng điểm bài kiểm tra môn Toán của lớp 10A được cho ở bảng sau:

Số trung vị của mẫu số liệu trên thuộc khoảng nào trong các nhóm dưới đây?
-
A.
[6; 8).
-
B.
[8; 10).
-
C.
[4; 6).
-
D.
[2; 4).



















Danh sách bình luận