Một cổng vòm được thiết kế dạng parabol \(y = a{x^2}\) như hình dưới đây. Biết chiều rộng của chân cổng là \(AB = 6m\) và chiều cao cổng là \(OI = 4,5m\).
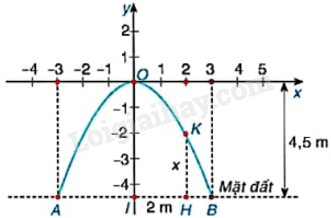
a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2m.
b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2m, chiều cao 3m. Hỏi xe tải này có thể đi qua được cổng vòm đó hay không?
a) + Đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(\left( {3;4,5} \right)\). Thay tọa độ điểm \(\left( {3;4,5} \right)\) vào hàm số \(y = a{x^2}\) ta tìm được a.
+ \(HK = \left| { - 4,5 - \left( { - \frac{1}{2}{{.2}^2}} \right)} \right|\)
b) So sánh chiều cao và chiều rộng của xe tải và với chiều cao và chiều rộng của cổng vòm. Từ đó rút ra kết luận.
a) Vì điểm \(\left( {3;4,5} \right)\) thuộc parabol nên ta có: \( - 4,5 = a{.3^2}\), suy ra \(a = - \frac{1}{2}\).
Từ đó ta có \(HK = \left| { - 4,5 - \left( { - \frac{1}{2}{{.2}^2}} \right)} \right| = 2,5\left( m \right)\).
b) Do xe tải có chiều rộng 2m nên ta tính chiều cao cổng tại vị trí cách I là 1m, tương ứng với \(x = 1\).
Tại \(x = 1\), chiều cao cổng là \(HK = \left| { - 4,5 - \left( { - \frac{1}{2}{{.1}^2}} \right)} \right| = 4\left( m \right)\).
Do chiều cao của cổng tại vị trí này lớn hơn chiều cao của xe tải nên xe tải này có thể đi qua được cổng vòm.

Các bài tập cùng chuyên đề
Bài 1 :
Kết luận nào sau đây là sai khi nói về đồ thị của hàm số $y = a{x^2}\,\,$ với $a \ne 0$.
-
A.
Đồ thị hàm số nhận trục tung làm trục đối xứng
-
B.
Với $a > 0$ đồ thị nằm phía trên trục hoành và $O$ là điểm cao nhất của đồ thị
-
C.
Với $a < 0$ đồ thị nằm phía dưới trục hoành và $O$ là điểm cao nhất của đồ thị
-
D.
Với $a > 0$ đồ thị nằm phía trên trục hoành và $O$ là điểm thấp nhất của đồ thị
Bài 2 :
Cho hàm số $y = f\left( x \right) = \left( { - 2m + 1} \right){x^2}.$
Tìm giá trị của $m$ để đồ thị đi qua điểm $A\left( { - 2;4} \right).$
-
A.
$m = 0$
-
B.
$m = 1$
-
C.
$m = 2$
-
D.
$m = - 2$
Bài 3 :
Cho hàm số \(y = \left( {2m + 2} \right){x^2}\). Tìm $m$ để đồ thị hàm số đi qua điểm $A\left( {x;y} \right)$ với $\left( {x;y} \right)$ là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x - y = 3\end{array} \right.\)
-
A.
$m = \dfrac{7}{4}$
-
B.
$m = \dfrac{1}{4}$
-
C.
$m = \dfrac{7}{8}$
-
D.
$m = - \dfrac{7}{8}$
Bài 4 :
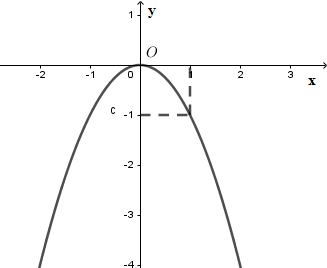
Hình vẽ dưới đây là của đồ thị hàm số nào?
-
A.
$y = - {x^2}$
-
B.
$y = {x^2}$
-
C.
$y = 2{x^2}$
-
D.
$y = - 2{x^2}$
Bài 5 :
Cho hàm số $y = \sqrt 3 {x^2}\,\,$có đồ thị là $(P)$. Có bao nhiêu điểm trên $\left( P \right)$ có tung độ gấp đôi hoành độ.
-
A.
$5$
-
B.
$4$
-
C.
$3$
-
D.
$2$
Bài 6 :
Trong các điểm $A(1;2);B( - 1; - 1);C(10; - 200);D\left( {\sqrt {10} ; - 10} \right)$ có bao nhiêu điểm thuộc đồ thị hàm số $\left( P \right): y = - {x^2}$
-
A.
$1$
-
B.
$4$
-
C.
$3$
-
D.
$2$
Bài 7 :
Cho $(P):y = \dfrac{1}{2}{x^2};(d):y = x - \dfrac{1}{2}$. Tìm toạ độ giao điểm của $(P)$ và $(d)$.
-
A.
$\left( {1;\dfrac{1}{2}} \right)$
-
B.
$\left( {1;2} \right)$
-
C.
$\left( {\dfrac{1}{2};1} \right)$
-
D.
$\left( {2;1} \right)$
Bài 8 :
Cho parabol \(y = \dfrac{1}{4}{x^2}\). Xác định \(m\) để điểm \(A\left( {\sqrt 2 ;m} \right)\) nằm trên parabol.
-
A.
\(m = \dfrac{1}{2}\)
-
B.
\(m = - \dfrac{1}{2}\)
-
C.
\(m = 2\)
-
D.
\(m = - 2\)
Bài 9 :
Cho parabol$(P):y = 2{x^2}$ và đường thẳng $(d):y = x + 1$. Số giao điểm của đường thẳng $d$ và parabol $\left( P \right)$ là:
-
A.
$1$
-
B.
$0$
-
C.
$3$
-
D.
$2$
Bài 10 :
Cho parabol $(P):y = \left( {m - 1} \right){x^2}$ và đường thẳng $(d):y = 3 - 2x$. Tìm $m$ để đường thẳng $d$ cắt $\left( P \right)$ tại điểm có tung độ $y = 5$.
-
A.
$m = 5$
-
B.
$m = 7$
-
C.
$m = 6$
-
D.
$m =-6$
Bài 11 :
Cho parabol $(P):y = \left( {\dfrac{{1 - 2m}}{2}} \right){x^2}$ và đường thẳng $(d):y = 2x + 2$. Biết đường thẳng $d$ cắt $\left( P \right)$ tại một điểm có tung độ $y = 4$. Tìm hoành độ giao điểm còn lại của $d$ và parabol $\left( P \right)$.
-
A.
$x = - \dfrac{1}{2}$
-
B.
$x = \dfrac{1}{2}$
-
C.
$x = - \dfrac{1}{4}$
-
D.
$x = \dfrac{1}{4}$
Bài 12 :
Cho hàm số \(y = f\left( x \right) = \dfrac{{2m - 3}}{3}{x^2}\) . Tìm giá trị của \(m\) để đồ thị đi qua điểm \(B\left( { - 3;5} \right)\)
-
A.
\(m = 1\)
-
B.
\(m = \dfrac{3}{7}\)
-
C.
\(m = \dfrac{7}{3}\)
-
D.
\(m = 3\)
Bài 13 :
Cho hàm số \(y = \left( { - 3m + 1} \right){x^2}\). Tìm \(m\) để đồ thị hàm số đi qua điểm \(A\left( {x;y} \right)\) với \(\left( {x;y} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x - 3y = - 2\\x - 2y = - 3\end{array} \right.\)
-
A.
\(m = \dfrac{1}{3}\)
-
B.
\(m = - \dfrac{1}{3}\)
-
C.
\(m = 3\)
-
D.
\(m = - 3\)
Bài 14 :
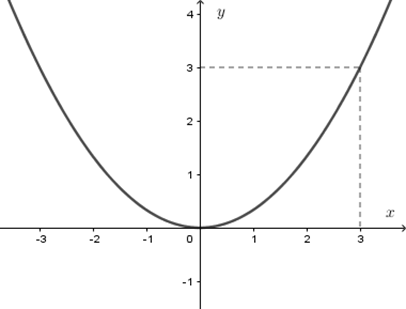
Hình vẽ dưới đây là của đồ thị hàm số nào?
-
A.
\(y = {x^2}\)
-
B.
\(y = \dfrac{1}{2}{x^2}\)
-
C.
\(y = 3{x^2}\)
-
D.
\(y = \dfrac{1}{3}{x^2}\)
Bài 15 :
Cho hàm số \(y = - \dfrac{2}{5}{x^2}\,\,\)có đồ thị là \((P)\). Điểm trên \(\left( P \right)\) (khác gốc tọa độ \(O\left( {0;0} \right)\)) có tung độ gấp ba lần hoành độ thì có hoành độ là:
-
A.
\(\dfrac{{15}}{2}\)
-
B.
\(\dfrac{{ - 15}}{2}\)
-
C.
\(\dfrac{2}{{15}}\)
-
D.
\( - \dfrac{2}{{15}}\)
Bài 16 :
Trong các điểm \(A(5;5);B( - 5; - 5);C(10;20);D\left( {\sqrt {10} ;2} \right)\) có bao nhiêu điểm không thuộc đồ thị hàm số \(y = \dfrac{1}{5}{x^2}\,\left( P \right)\)
-
A.
\(1\)
-
B.
\(4\)
-
C.
\(3\)
-
D.
\(2\)
Bài 17 :
Cho \((P):y = 3{x^2};(d):y = - 4x - 1\). Tìm toạ độ giao điểm của \((P)\) và \((d)\).
-
A.
\(\left( {\dfrac{1}{3}; - \dfrac{1}{3}} \right);\left( {1;3} \right)\)
-
B.
\(\left( {\dfrac{1}{3};\dfrac{1}{3}} \right);\left( {1;3} \right)\)
-
C.
\(\left( { - \dfrac{1}{3};\dfrac{1}{3}} \right);\left( { - 1;3} \right)\)
-
D.
\(\left( { - \dfrac{1}{3};\dfrac{1}{3}} \right)\)
Bài 18 :
Cho parabol \(y = - \sqrt 5 {x^2}\). Xác định m để điểm \(A\left( {m\sqrt 5 ; - 2\sqrt 5 } \right)\) nằm trên parabol.
-
A.
\(m = - \dfrac{5}{2}\)
-
B.
\(m =- \dfrac{\sqrt 10}{5}.\)
-
C.
\(m = \dfrac{\sqrt 10}{5}.\)
-
D.
\(m =\pm \dfrac{\sqrt 10}{5}\)
Bài 19 :
Cho parabol\((P):y = \sqrt {5m + 1} .{x^2}\) và đường thẳng \((d):y = 5x + 4\). Tìm \(m\) để đường thẳng \(d\) cắt \(\left( P \right)\) tại điểm có tung độ \(y = 9\).
-
A.
\(m = 5\)
-
B.
\(m = 15\)
-
C.
\(m = 6\)
-
D.
\(m = 16\)
Bài 20 :
Cho parabol\((P):y = \left( {\sqrt {3m + 4} - \dfrac{7}{4}} \right){x^2}\) và đường thẳng \((d):y = 3x - 5\). Biết đường thẳng \(d\) cắt \(\left( P \right)\) tại một điểm có tung độ \(y = 1\). Tìm \(m\) và hoành độ giao điểm còn lại của \(d\) và parabol \(\left( P \right)\).
-
A.
\(m = 0;x = 2\)
-
B.
\(m = \dfrac{1}{4};x = - 10\)
-
C.
\(m = 2;x = 8\)
-
D.
\(m = 0;x = 10\)
Bài 21 :
Cho parabol\((P):y = 5{x^2}\) và đường thẳng \((d):y = - 4x - 4\). Số giao điểm của đường thẳng \(d\) và parabol \(\left( P \right)\) là:
-
A.
\(1\)
-
B.
\(0\)
-
C.
\(3\)
-
D.
\(2\)
Bài 22 :
Xác định hàm số \(y = a{x^2}\) biết rằng đồ thị của hàm số đi qua điểm \(A\left( { - 2;5} \right)\).
-
A.
\(y = \dfrac{5}{4}x^2\)
-
B.
\(y = \dfrac{4}{5}x^2\)
-
C.
\(y = x^2\)
-
D.
\(y = \dfrac{5}{2}x^2\)
Bài 23 :
Biết đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(A\left( { - 1; - 2} \right),\) giá trị của \(a\) bằng:
-
A.
\(a = - \dfrac{1}{2}\)
-
B.
\(a = - 2\)
-
C.
\(a = 2\)
-
D.
\(a = \dfrac{1}{2}\)
Bài 24 :
Tìm tọa độ giao điểm của đồ thị hai hàm số \(y = - {x^2}\) và \(y = x - 2\)
-
A.
\(\left ( - 1; - 1 \right )\,;\,\,\left ( - 2; - 4 \right )\)
-
B.
\(\left ( 1; - 1 \right )\,;\,\,\left ( 2; - 4 \right )\)
-
C.
\(\left ( 1; - 1 \right )\,;\,\,\left ( - 2; - 4 \right )\)
-
D.
\(\left ( - 1; - 1 \right )\,;\,\,\left ( 2; - 4 \right )\)
Bài 25 :
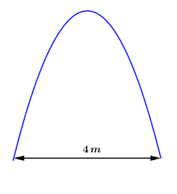
Cổng vào một ngôi biệt thự có hình dạng là một parabol được biểu diễn bởi đồ thị hàm số \(y = - {x^2}.\) Biết khoảng cách giữa hai chân cổng là \(4\,m.\) Một chiếc ô tô tải có thùng xe là một hình hộp chữ nhật có chiều rộng là \(2,4\,m.\) Hỏi chiều cao lớn nhất có thể của ô tô là bao nhiêu để ô tô có thể đi qua cổng?
-
A.
\(2,\,4\,m\)
-
B.
\(1,44\,m\)
-
C.
\(4\,m\)
-
D.
\(2,56\,m\)
Bài 26 :
Đồ thị hàm số \(y = \dfrac{1}{4}{x^2}\) đi qua điểm
-
A.
\(M\left( {2; - 1} \right)\)
-
B.
\(N\left( {2;\dfrac{1}{2}} \right)\)
-
C.
\(P\left( {2; - \dfrac{1}{2}} \right)\)
-
D.
\(Q\left( {2;1} \right)\)
Bài 27 :
Cho hàm số \(y = a{x^2}\) có đồ thị như hình vẽ bên. Hàm số đó là:
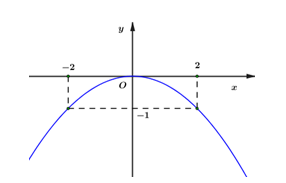
-
A.
\(y = \dfrac{1}{2}{x^2}\)
-
B.
\(y = - \dfrac{1}{2}{x^2}\)
-
C.
\(y = - \dfrac{1}{4}{x^2}\)
-
D.
\(y = \dfrac{1}{4}{x^2}\)
Bài 28 :
Đồ thị trong hình bên là của hàm số:
-
A.
\(y = - \dfrac{1}{2}{x^2}\)
-
B.
\(y = \dfrac{1}{2}{x^2}\)
-
C.
\(y = 2{x^2}\)
-
D.
\(y = - 2{x^2}\)
Bài 29 :
Tìm \(m\) để đồ thị hàm số \(y = \left( {m + 5} \right){x^2}\) đi qua điểm \(A\left( { - 1;\,\,2} \right).\)
-
A.
\(m = - 3\)
-
B.
\(m = 6\)
-
C.
\(m = 3\)
-
D.
\(m = - 7\)
Bài 30 :
Tìm \(m\) để đồ thị hàm số \(y = \left( {2m + 1} \right){x^2}\) đi qua điểm \(A\left( {1;5} \right)\).
-
A.
\(m = 0\)
-
B.
\(m = 1\)
-
C.
\(m = 2\)
-
D.
\(m = - 1\)


















Danh sách bình luận