Vẽ đồ thị các hàm số bậc hai sau:
a) \(y = - {x^2} + 4x - 3\)
b) \(y = {x^2} + 2\)
c) \(y = \frac{1}{2}{x^2} + x + 1\)
d) \(y = {x^2} - 4x + 4\)
Bước 1: Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
Bước 2: Nhập phương trình bậc hai cần vẽ hình
a)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=-x^2+4x-3 vào vùng nhập lệnh như hình bên
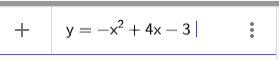
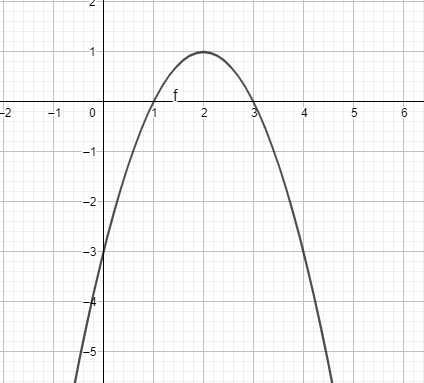
Ta có ngay parabol trên vùng làm việc như hình dưới:
b)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2+2 vào vùng nhập lệnh như hình bên
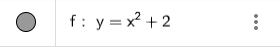
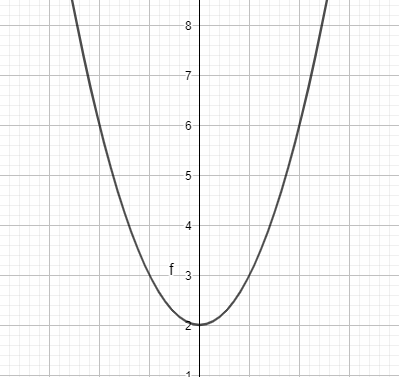
Ta có ngay parabol trên vùng làm việc như hình dưới:
c)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=1/2x^2+x+1 vào vùng nhập lệnh như hình bên
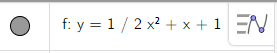
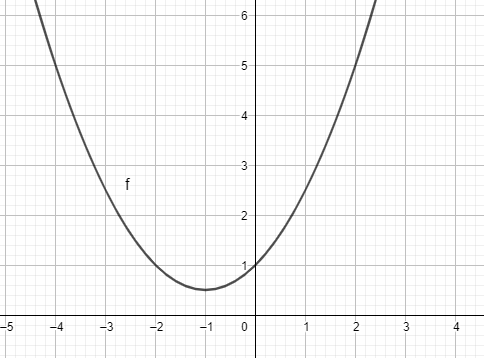
Ta có ngay parabol trên vùng làm việc như hình dưới:
d)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2-4x+4 vào vùng nhập lệnh như hình bên
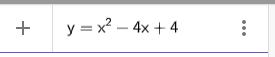
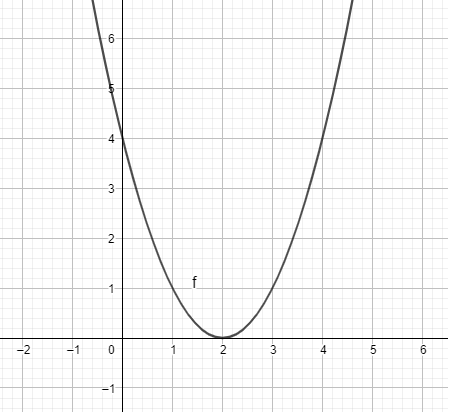
Ta có ngay parabol trên vùng làm việc như hình dưới:

Các bài tập cùng chuyên đề
Bài 1 :
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau:
\(\left\{ \begin{array}{l}x - 2y + 3 \le 0\\x + 3y > - 2\\x \le 0\end{array} \right.\)
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau:
Bài 2 :
Điều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau:
a) \(\)\(y = {x^2} - 3x + 2\)
b) \(y = {x^2}\)
c) \(y = - {x^2}\)
d) \(y = 2{x^2} + 1\)
e) \(y = - \frac{1}{2}{x^2} + 4\)
Bài 3 :
Hãy tự thiết kế một cổng chào hình parabol.


















Danh sách bình luận