Biểu thức \(\sqrt {{{\left( {3 - 2x} \right)}^2}} \) bằng
-
A.
\(3 - 2x\).
-
B.
\(2x - 3\).
-
C.
\(\left| {2x - 3} \right|\).
-
D.
\(3x - 2\) và \(2 - 3x\).
Sử dụng công thức \(\sqrt {{A^2}} = \left| A \right|\).
\(\sqrt {{{\left( {3 - 2x} \right)}^2}} = \left| {3 - 2x} \right| = \left| {2x - 3} \right|\).
Đáp án C.
Đáp án : C

Các bài tập cùng chuyên đề
Bài 1 :
Rút gọn biểu thức $A = \sqrt {36{a^2}} + 3a$ với $a > 0$.
-
A.
$ - 9a$
-
B.
$ - 3a$
-
C.
$ 3a$
-
D.
$ 9a$
Bài 2 :
Rút gọn biểu thức
$\sqrt {{a^2} + 8a + 16} + \sqrt {{a^2} - 8a + 16} $ với $ - 4 \le a \le 4$ ta được
-
A.
$2a$
-
B.
$8$
-
C.
$ - 8$
-
D.
$ - 2a$
Bài 3 :
Nghiệm của phương trình \(\sqrt {{x^2} + 6x + 9} = 4 - x\) là
-
A.
$x = 2$
-
B.
$x = \dfrac{1}{4}$
-
C.
$x = \dfrac{1}{2}$
-
D.
$x = 3$
Bài 4 :
Rút gọn biểu thức $\dfrac{{\sqrt {{x^2} - 6x + 9} }}{{x - 3}}$ với $x < 3$ ta được
-
A.
$ - 1$
-
B.
$ 1$
-
C.
$ 2$
-
D.
$ - 2$
Bài 5 :
Tìm giá trị nhỏ nhất của biểu thức \(A = \sqrt {{m^2} + 2m + 1} + \sqrt {{m^2} - 8m + 16} \).
-
A.
$2$
-
B.
$9$
-
C.
$5$
-
D.
$10$
Bài 6 :
Rút gọn biểu thức \(A = \sqrt {144{a^2}} - 9a\) với \(a > 0\).
-
A.
\( - 9a\)
-
B.
\( - 3a\)
-
C.
\(3a\)
-
D.
\(9a\)
Bài 7 :
Rút gọn biểu thức \(\sqrt {4{a^2} + 12a + 9} + \sqrt {4{a^2} - 12a + 9} \) với \( - \dfrac{3}{2} \le a \le \dfrac{3}{2}\) ta được:
-
A.
\( - 4a\)
-
B.
\(4a\)
-
C.
\( - 6\)
-
D.
\(6\)
Bài 8 :
Số nghiệm của phương trình \(\sqrt {4{x^2} + 4x + 1} = 3 - 4x\) là:
-
A.
\(0\)
-
B.
\(4\)
-
C.
\(1\)
-
D.
\(2\)
Bài 9 :
Rút gọn biểu thức \(\dfrac{{\sqrt {{x^2} + 10x + 25} }}{{ - 5 - x}}\) với \(x < - 5\) ta được:
-
A.
\( - 1\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
\(-2\)
Bài 10 :
Tìm giá trị nhỏ nhất của biểu thức \(B = \sqrt {4{a^2} - 4a + 1} + \sqrt {4{a^2} - 12a + 9} \).
-
A.
\(2\)
-
B.
\(1\)
-
C.
\(4\)
-
D.
\(10\)
Bài 11 :
Rút gọn \(A = \dfrac{{\sqrt {x - 1 - 2\sqrt {x - 2} } }}{{\sqrt {x - 2} - 1}}\) với \(x > 3\)
-
A.
\(A = \sqrt x - 2\)
-
B.
\(A = 1\)
-
C.
\(A = - 1\)
-
D.
Kết quả khác.
Bài 12 :
Rút gọn biểu thức sau \(\sqrt {{{\left( {a - b} \right)}^2}} - 3\sqrt {{a^2}} + 2\sqrt {{b^2}} \) với \(a < 0 < b\)
-
A.
\( - 2a + b\)
-
B.
\(3b - 2a\)
-
C.
\(2a + 3b\)
-
D.
\(a + b\)
Bài 13 :
a) Rút gọn biểu thức \(x\sqrt {{x^6}} \left( {x < 0} \right).\)
b) Rút gọn và tính giá trị của biểu thức \(x + \sqrt {4{x^2} - 4x + 1} \) tại \(x = - 2,5.\)
Bài 14 :
Rút gọn các biểu thức sau:
a) \(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} ;\)
b) \(3\sqrt {{x^2}} - x + 1\left( {x < 0} \right);\)
c) \(\sqrt {{x^2} - 4x + 4} \left( {x < 2} \right).\)
Bài 15 :
Tìm x, biết:
a) x2 = 121
b) 4x2 = 9
c) x2 = 10
Bài 16 :
Hoàn thành bảng sau vào vở.

Từ đó, nhận xét gì về căn bậc hai số học của bình phương của một số?
Bài 17 :
Tính
a) \(\sqrt {{{\left( { - 0,4} \right)}^2}} \)
b) \( - \sqrt {{{\left( { - \frac{4}{9}} \right)}^2}} \)
c) \( - 2\sqrt {{3^2}} + {\left( { - \sqrt 6 } \right)^2}\)
Bài 18 :
Rút gọn các biểu thức sau:
a) \(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \)
b) \(\sqrt {{a^2}} + \sqrt {{{( - 3a)}^2}} \) với a > 0.
Bài 19 :
Tìm chỗ sai trong phép chứng minh “voi con nặng bằng voi mẹ” sau đây:
\(\begin{array}{l}{M^2} - 2Mm + {m^2} = {m^2} - 2mM + {M^2}\\{(M - m)^2} = {(m - M)^2}\\\sqrt {{{(M - m)}^2}} = \sqrt {{{(m - M)}^2}} \\M - m = m - M\\2M = 2m\\M = m(!)\end{array}\)
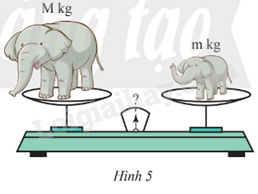
Bài 20 :
Biết rằng 1 < a < 5, rút gọn biểu thức
A = \(\sqrt {{{\left( {a - 1} \right)}^2}} + \sqrt {{{\left( {a - 5} \right)}^2}} \).
Bài 21 :
Tìm số thích hợp cho “?”:
a. \(\sqrt {7_{}^2} = ?\);
b. \(\sqrt {\left( { - 9} \right)_{}^2} = ?\);
c. \(\sqrt {a_{}^2} = ?\) với a là một số cho trước.
Bài 22 :
Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức:
a. \(\sqrt {x_{}^2 + 6x + 9} \) với \(x < - 3\);
b. \(\sqrt {y_{}^4 + 2y_{}^2 + 1} \).
Bài 23 :
Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức:
a. \(\sqrt {\left( {5 - x} \right)_{}^2} \) với \(x \ge 5\);
b. \(\sqrt {\left( {x - 3} \right)_{}^4} \);
c. \(\sqrt {\left( {y + 1} \right)_{}^6} \) với \(y < - 1\).
Bài 24 :
Rút gọn biểu thức:
a. \(A = \sqrt {40_{}^2 - 24_{}^2} \);
b. \(B = \left( {\sqrt {12} + 2\sqrt 3 - \sqrt {27} } \right).\sqrt 3 \);
c. \(C = \frac{{\sqrt {63_{}^3 + 1} }}{{\sqrt {63_{}^2 - 62} }}\);
d. \(D = \sqrt {60} - 5\sqrt {\frac{3}{5}} - 3\sqrt {\frac{5}{3}} \).
Bài 25 :
Hãy chép lại và hoàn thành Bảng 3.1. Em có nhận xét gì về giá trị của \(\sqrt {{{\left( {2x - 1} \right)}^2}} \) và \(\left| {2x - 1} \right|\)?

Bài 26 :
Rút gọn:
a) \(\sqrt {{x^8}} \);
b) \(2\sqrt {{{\left( { - y + 5} \right)}^2}} \) với \(y \ge 5\);
c) \( - 3\sqrt {{z^{10}}} \) với \(z < 0\).
Bài 27 :
Rút gọn rồi tính giá trị biểu thức \(\sqrt {25{{\left( {4{x^2} - 4x + 1} \right)}^2}} \) tại \(x = \sqrt 3 \).
Bài 28 :
Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức:
a) \(\sqrt {25 - 10 + {x^2}} \) với \(x \le 5.\)
b) \(\sqrt {{{\left( {9 + 12x + 4{x^2}} \right)}^2}} \)
c) \(\sqrt {{{\left( {3x + 1} \right)}^6}} \) với \(x \ge \frac{{ - 1}}{3}\)
d) \(\sqrt {\frac{{49{x^2}{{\left( {x + 5} \right)}^2}}}{{16}}} \) với \(x \ge 0\)
Bài 29 :
Tìm x, biết:
a) \(\frac{1}{2}\sqrt x - \frac{3}{2}\sqrt {9x} + 24\sqrt {\frac{x}{{64}}} = - 17\) với \(x \ge 0\)
b) \(\sqrt {\frac{x}{5}} = 4\) với \(x \ge 0\)
c) \(\sqrt {25{x^2}} = 10\)
d) \(\sqrt {{{\left( {2x - 1} \right)}^2}} = 3\)
e) \(2 - \sqrt[3]{{5 - x}} = 0\)
Bài 30 :
Rút gọn biểu thức \(\sqrt {{{\left( { - a} \right)}^2}} - \sqrt {9{a^2}} \) với a < 0, ta có kết quả
A. – 4a
B. 2a
C. 4a
D. – 2a


















Danh sách bình luận