Máy kéo nông nghiệp có hai loại bánh xe, trong đó bánh sau to hơn bánh trước. Khi bơm căng, bánh sau có đường kính là 1,672m và bánh trước có đường kính là 88cm. Hỏi bánh xe sau lăn được 20 vòng thì bánh trước lăn được bao nhiêu vòng?
Sử dụng công thức tính chu vi đường tròn: \(C = 2\pi R = \pi d\) (R là bán kính của đường tròn, d là đường kính).
Cứ một vòng quay của bánh xe thì xe đi được quãng đường bằng chu vi của bánh nên ta tính được quãng đường đi được khi bánh sau lăn được 20 vòng = chu vi.20.
Số vòng bánh trước lăn được = quãng đường đi được : chu vi 1 vòng bánh trước.
Chu vi của bánh xe sau là:
\({C_{sau}} = \pi .{d_{sau}} = 1,672\pi \left( m \right) = 167,2\pi \left( {cm} \right)\).
Khi bánh xe sau lăn được 20 vòng thì đi được quãng đường là:
\(167,2\pi .20 = 3344\pi \left( {cm} \right)\)
Chu vi của bánh trước là:
\({C_{tr}} = \pi .{d_{tr}} = 88\pi \left( {cm} \right)\).
Cứ một vòng quay của bánh xe sau, thì xe đi được quãng đường bằng chu vi của bánh xe.
Do đó khi bánh xe sau lăn được 20 vòng thì xe di chuyển được đoạn đường là:
\(3344\pi :\left( {88\pi } \right) = 38\) (vòng).
Vậy bánh xe sau lăn được 20 vòng thì bánh trước lăn được 38 vòng.
Các bài tập cùng chuyên đề
Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d, C và D lần lượt là điểm đối xứng với A và B qua O.
a) Ba điểm B, C và D có thuộc (O) hay không? Vì sao?
b) Chứng minh tứ giác ABCD là hình chữ nhật.
c) Chứng minh rằng C và D đối xứng với nhau qua d.
Cho hình vuông ABCD có E là giao điểm của hai đường chéo.
a) Chứng minh rằng chỉ có một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm đối xứng và chỉ ra hai trục đối xứng của đường tròn đó.
b) Tính bán kính của đường tròn ở câu a, biết rằng hình vuông có cạnh bằng 3 cm.
Xác định tâm đối xứng và trục đối xứng của bánh xe trong Hình 7. Giải thích cách làm.
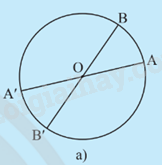
a) Cho đường tròn (O;R).
i) Lấy điểm A nằm trên đường tròn. Vẽ đường thẳng AO cắt đường tròn tại điểm A’ khác A. Giải thích tại sao O là trung điểm của đoạn thẳng AA’.
ii) Lấy điểm B khác A thuộc đường tròn (O;R). Tìm điểm B’ sao cho O trung điểm của đoạn thẳng BB’. Điểm B’ có thuộc đường tròn (O;R) không? Giải thích.
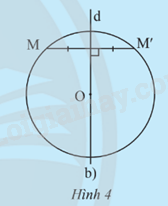
b) Cho đường tròn (O;R), d là đường thẳng đi qua tâm O. Lấy điểm M nằm trên đường tròn. Vẽ điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (khi M thuộc d thì lấy M’ trùng với M). Điểm M’ có thuộc đường tròn (O;R) không? Giải thích.
Cho đoạn thẳng \(MN\) và đường thẳng \(a\) là đường trung trực của đoạn thẳng \(MN\). Điểm \(O\) thuộc đường thẳng \(a\).
a) Vẽ đường tròn tâm \(O\) bán kính \(R = OM\).
b) Chứng minh điểm \(N\) thuộc đường tròn \(\left( {O;R} \right)\).
Cho đường tròn \(\left( {O;R} \right)\) và dây \(AB\) khác đường kính. Gọi \(M\) là trung điểm của \(AB\).
a) Đường thẳng \(OM\) có phải là đường trung trực của đoạn thẳng \(AB\) hay không? Vì sao?
b) Tính khoảng cách từ điểm \(O\) đến đường thẳng \(AB\), biết \(R = 5cm,AB = 8cm\).
Hai đường tròn có bao nhiêu trục đối xứng nếu chúng:
a) Có cùng tâm?
b) Không cùng tâm?
Khẳng định nào sau đây là sai?
Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d; C và D lần lượt là điểm đối xứng với A và B qua O.
a) Ba điểm B, C và D có thuộc (O) không? Vì sao?
b) Chứng minh tứ giác ABCD là hình chữ nhật.
c) Chứng minh rằng C và D đối xứng với nhau qua d.
Cho hình vuông ABCD có E là giao điểm của hai đường chéo.
a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm đối xứng và chỉ ra hai trục đối xứng của đường tròn đó.
b) Tính bán kính của đường tròn ở câu a, biết rằng hình vuông có cạnh bằng 3cm.
Đường tròn là hình
