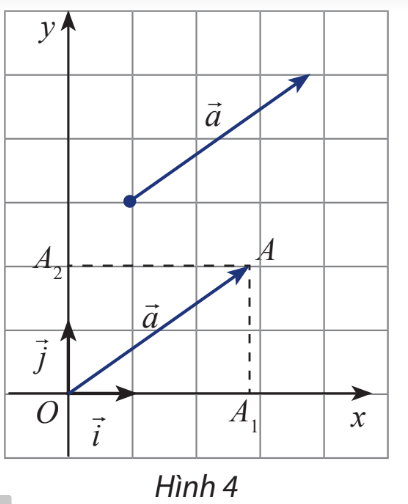
Trong mặt phẳng Oxy, cho một vectơ \(\overrightarrow a \)tùy ý. Vẽ \(\overrightarrow {OA} = \overrightarrow a \)và gọi \({A_1},{A_2}\)lần lượt là hình chiếu vuông góc của A lên Ox và Oy (hình 4). Đặt \({\overrightarrow {OA} _1} = x\overrightarrow i \), \({\overrightarrow {OA} _2} = y\overrightarrow j \). Biểu diễn vectơ \(\overrightarrow a \)theo hai vectơ và \(\overrightarrow j \).
Bước 1: Áp dụng quy tắc hình bình hành \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \).
Bước 2: Dựa vào hình vẽ tìm x,y.
Bước 3: Biểu diễn vectơ \(\overrightarrow a \).
Áp dụng quy tắc hình bình hành ta có \(\overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} \).
Dựa vào hình vẽ ta thấy \({\overrightarrow {OA} _1} = 3\overrightarrow i \) và \({\overrightarrow {OA} _2} = 2\overrightarrow j \).
Vậy \(\overrightarrow a = \overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} = 3\overrightarrow i + 2\overrightarrow j \).

Các bài tập cùng chuyên đề
Bài 1 :
Cho hình vuông $ABCD$, khẳng định nào sau đây đúng:
-
A.
$\overrightarrow {AC} = \overrightarrow {BD} $.
-
B.
$\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|$.
-
C.
$\overrightarrow {AB} = \overrightarrow {CD} $.
-
D.
$\overrightarrow {AB} $ và $\overrightarrow {AC} $ cùng hướng.
Bài 2 :
Cho tam giác đều ABC. Mệnh đề nào sau đây sai?
-
A.
$\overrightarrow {AB} = \overrightarrow {BC} $
-
B.
$\overrightarrow {AC} \ne \overrightarrow {BC} $
-
C.
$\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|$
-
D.
$\overrightarrow {AC} $ không cùng phương $\overrightarrow {BC} $
Bài 3 :
Gọi \(O\) là giao điểm của hai đường chéo hình chữ nhật \(ABCD\). Mệnh đề nào sau đây đúng?
-
A.
\(\overrightarrow {OA} = \overrightarrow {OC} .\)
-
B.
\(\overrightarrow {OB} \) và \(\overrightarrow {OD} \) cùng hướng.
-
C.
\(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) cùng hướng.
-
D.
\(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BD} } \right|.\)
Bài 4 :
Cho tam giác đều ABC. Mệnh đề nào sau đây đúng ?
-
A.
\(\overrightarrow {AB} = \overrightarrow {BC} \)
-
B.
\(\overrightarrow {AC} = \overrightarrow {BC}\)
-
C.
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|\)
-
D.
\(\overrightarrow {AC} \) cùng hướng \(\overrightarrow {BC}\)
Bài 5 :
Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)đều khác \(\overrightarrow 0 \). Những khẳng định nào sau đây là đúng?
a) \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đều cùng hướng với vectơ \(\overrightarrow 0 \);
b) Nếu \(\overrightarrow b \)không cùng hướng với \(\overrightarrow a \) thì \(\overrightarrow b \) ngược hướng với \(\overrightarrow a \).
c) Nếu \(\overrightarrow a \) và \(\overrightarrow b \) đều cùng phương với \(\overrightarrow c \) thì \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương.
d) Nếu \(\overrightarrow a \) và \(\overrightarrow b \) đều cùng hướng với \(\overrightarrow c \) thì \(\overrightarrow a \)và \(\overrightarrow b \) cùng hướng.
Bài 6 :
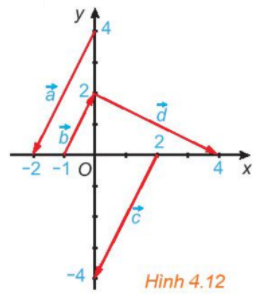
Trong Hình 4.12, hãy chỉ ra các vecto cùng phương, các cặp vecto ngược hướng và các cặp vecto bằng nhau.
Bài 7 :
Trên mặt phẳng tọa độ Oxy hãy vẽ các vecto \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) với A (1; 2), M (0; -1), N (3; 5).
a) Chỉ ra mỗi quan hệ giữa hai vecto trên.
b) Một vật thể khởi hành từ M chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn vởi vecto \(\overrightarrow v = \overrightarrow {OA} \). Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu sẽ tới N?
Bài 8 :
Cho đoạn thẳng MN có trung điểm là I.
a) Viết các vectơ khác vectơ-không có điểm đầu, điểm cuối là một trong ba điểm M, N, I.
b) vectơ nào bằng \(\overrightarrow {MI} \)? Bằng \(\overrightarrow {NI} \)?
Bài 9 :
Cho hình thang ABCD có hai đáy là AB và CD. Tìm vectơ:
a) Cùng hướng với \(\overrightarrow {AB} \)
b) Ngược hướng với \(\overrightarrow {AB} \)
Bài 10 :
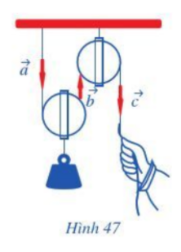
Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)(Hình 47).
a) Hãy chỉ ra các cặp vectơ cùng phương.
b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.
Bài 11 :
Hãy chỉ ra các cặp vectơ cùng hướng, ngược hướng, bằng nhau trong hình 17.
Bài 12 :
Gọi O là tâm hình lục giác đều ABCDEF.
a) Tìm các vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \).
b) Tìm các vectơ bằng vectơ \(\overrightarrow {AB} \).
Bài 13 :
Cho trước hai vectơ không cùng hướng \(\overrightarrow a \) và \(\overrightarrow b \). Hỏi có hay không một vectơ cùng phương với cả \(\overrightarrow a \) và \(\overrightarrow b \)?
Bài 14 :
Cho ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) cùng phương và cùng khác vectơ \(\overrightarrow 0 \). Chứng minh rằng có ít nhất hai vectơ trong chúng có cùng hướng.
Bài 15 :
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Xét các vectơ có hai điểm mút lấy từ các điểm \(O,\,\,A,\,\,B,\,\,C,\,\,D,\,\,E,\,\,F\).
a) Hãy chỉ ra các vectơ khác vectơ – không và cùng phương với vectơ \(\overrightarrow {OA} \).
b) Tìm các vectơ bằng vectơ \(\overrightarrow {AB} \).
Bài 16 :
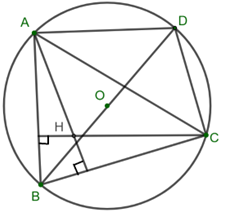
Cho tam giác \(ABC\) không vuông, với trực tâm \(H\), nội tiếp đường tròn \((O).\) Kẻ đường kính \(AA'\) của đường tròn \((O).\)
a) Chứng minh rằng \(\overrightarrow {BH} = \overrightarrow {A'C} .\)
b) Gọi \(M\) là trung điểm của \(BC.\) Tìm mối quan hệ về phương, hướng và độ dài của hai vectơ \(\overrightarrow {AH} \) và \(\overrightarrow {OM} .\)
Bài 17 :
Cho hình thoi \(ABCD\) có độ dài các cạnh bằng 1 và \(\widehat {DAB} = {120^ \circ }.\) Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AB} = \overrightarrow {CD} \)
B. \(\overrightarrow {BD} = \overrightarrow {AC} \)
C. \(\left| {\overrightarrow {BD} } \right| = 1\)
D. \(\left| {\overrightarrow {AC} } \right| = 1\)
Bài 18 :
Cho hình thang ABCD có AB và CD song song với nhau. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {AB} = \overrightarrow {CD} \)
B. \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng
C. \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng
D. \(\overrightarrow {AB} = \overrightarrow {DC} \)
Bài 19 :
Cho hình vuông ABCD có cạnh bằng a. Tính \(\left| {\overrightarrow {AB} } \right|,\left| {\overrightarrow {AC} } \right|\).
Bài 20 :
Cho đường tròn tâm O và dây cung BC không đi qua O. Điểm A chuyển động trên cung lớn BC của đường tròn sao cho tam giác ABC nhọn. Gọi H là trực tâm của tam giác ABC. Chứng minh rằng \(\overrightarrow {AH} \) có độ dài không đổi.
Bài 21 :
Cho hình chữ nhật ABCD có tâm O là giao điểm của hai đường chéo. Hãy chi ra một cặp vectơ
a) Cùng hướng
b) Ngược hướng
c) Bằng nhau
Bài 22 :
Cho hình chữ nhật ABCD có \(AB = 3,BC = 4\). Độ dài của vectơ \(\overrightarrow {AC} \) là:
A. 5
B. 6
C. 7
D. 9
Bài 23 :
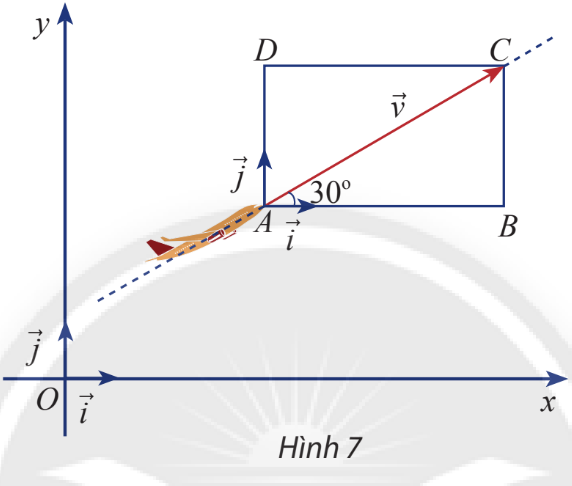
Một máy bay đang cất cánh với vận tốc 240 km/h theo phương hợp với phương nằm ngang một góc \(30^\circ \) (hình 7).
a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD.
b) Biểu diễn vận tốc \(\overrightarrow v \) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \).
c) Tìm tọa độ của \(\overrightarrow v \).
Bài 24 :
Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\).
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy.
b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \).
c) Vẽ và tìm tọa độ hai vectơ đơn vị \(\overrightarrow i \) và \(\overrightarrow j \) lần lượt trên hai trục tọa độ Ox và Oy.
Bài 25 :
Nêu nhận xét về độ lớn, phương và chiều của vectơ trên trục \(Ox\) và vectơ \(\overrightarrow j \) trên trục \(Oy\) (hình 1).

Bài 26 :
Chứng minh rằng:
a) \(\overrightarrow a = \left( {4; - 6} \right)\) và \(\overrightarrow b = \left( { - 2;3} \right)\) là hai vectơ ngược hướng.
b) \(\overrightarrow a = \left( { - 2;3} \right)\) và \(\overrightarrow b = \left( { - 8;12} \right)\) là hai vectơ cùng hướng.
c) \(\overrightarrow a = \left( {0;4} \right)\) và \(\overrightarrow b = \left( {0; - 4} \right)\) là hai vectơ đối nhau.
Bài 27 :
Hãy nhắc lại công thức tính khoảng cách giữa 2 điểm \(I\left( {a;b} \right)\) và \(M\left( {x;y} \right)\) trong mặt phẳng Oxy.



















Danh sách bình luận