Đề bài

Một bể chứa ban đầu có 100 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 20 lít nước, đồng thời cho vào bể 10 gam chất khử trùng (hòa tan). Nồng độ chất khử trùng (gam/lít) sau 10 phút là bao nhiêu (làm tròn đến hàng phần trăm)?

Đáp án:

Đáp án

Đáp án:

Phương pháp giải

Lập hàm số f(t) tính nồng độ chất khử (khối lượng chất khử trên thể tích nước) theo thời gian t phút rồi tính f(10).

Số lít nước trong bể chứa sau t phút là 100 + 20t (lít).

Số gam chất tan được cho vào bể sau t phút là 10t (gam).

Nồng độ chất khử trùng trong bể sau t phút là \(f(t) = \frac{{10t}}{{100 + 20t}} = \frac{t}{{10 + 2t}}\) (gam/lít).

Nồng độ chất khử trùng trong bể sau 10 phút là \(f(10) = \frac{{10}}{{10 + 2.10}} = \frac{1}{3} \approx 0,33\) (gam/lít).

Báo lỗi - Góp ý

BÌNH LUẬN

Danh sách bình luận

Đang tải bình luận...

Các bài tập cùng chuyên đề

Bài 1 :

Một cốc chứa 30ml dung dịch KOH (potassium hydroxide) với nồng độ 100mg/ml. Một bình chứa dung dịch KOH khác chứa nồng độ 8mg/ml được trộn vào cốc.

a) Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, kí hiệu là C(x).

b) Coi hàm C(x) là hàm số xác định với \(x \ge 0\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.

c) Giải thích tại sao nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8mg/ml.

Xem lời giải >>

Bài 2 :

Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên trần nhà lần lượt buộc vào ba điểm A, B, C trên đèn tròn sao cho tam giác ABC đều (Hình 38). Độ dài của ba đoạn dây OA, OB, OC đều bằng L. Trọng lượng của chiếc đèn là 24 N và bán kính của chiếc đèn là 18 in (1 inch 2,54 cm). Gọi F là độ lớn của các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) trên mỗi sợi dây. Khi đó, F = F(L) là một hàm số với biến số là L.

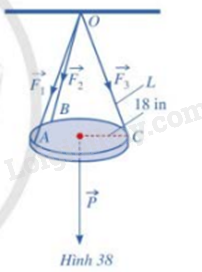
a) Xác định công thức tính hàm số F = F(L).

b) Khảo sát và vẽ đồ thị hàm số F = F(L).

c) Tìm chiều dài tối thiểu của mỗi sợi dây, biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là 10 N.

Xem lời giải >>

Bài 3 :

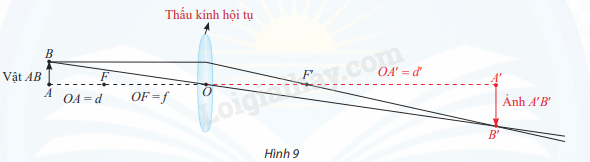
Xét một vật thật đặt trước thấu kính hội tụ có tiêu cự f > 0. Gọi d là khoảng cách từ vật đến thấu kính (d > 0), d’ là khoảng cách từ thấu kính đến ảnh (ảnh thật thì d’ > 0, ảnh ảo thì d’ < 0). Ta có công thức:

\(\frac{1}{f} = \frac{1}{d} + \frac{1}{{{d'}}}\) hay \(d' = \frac{{df}}{{d - f}}\)

(Vật lí 11, Nhà xuất bản Giáo dục Việt Nam, 2012, trang 182, 187)

Xét trường hợp f = 3, đặt x = d, y = d’. Ta có hàm số \(y = \frac{{3x}}{{x - 3}}\) và \(x \ne 3\).

a) Khảo sát và vẽ đồ thị của hàm số trên.

b) Dựa vào đồ thị hàm số trên, hãy cho biết vị trí của vật để ảnh của vật là: ảnh thật, ảnh ảo.

c) Khi vật tiến gần đến tiêu điểm thì ảnh thay đổi như thế nào?

Xem lời giải >>

Bài 4 :

Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b.

a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là: \(r = \frac{{5(12 - h)}}{{12}}\).

b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h: \(V(h) = \frac{{25\pi h{{(12 - h)}^2}}}{{144}}\).

c) Tìm h để khối trụ có thể tích lớn nhất.

Xem lời giải >>

Bài 5 :

Tìm hai số có hiệu là 13 sao cho tích của chúng bé nhất. Tổng hai số đó bằng bao nhiêu?

Xem lời giải >>

Bài 6 :

Hàm chi phí và hàm doanh thu (đều tính bằng triệu đồng) của một loại sản phẩm lần lượt là \(C\left( x \right) = 25,5x + 1000\) và \(R\left( x \right) = 75,5x\), trong đó \(x\)là số đơn vị sản phẩm đó được sản xuất và bán ra.

a) Tìm hàm lợi nhuận trung bình \(\bar P\left( x \right) = \frac{{R\left( x \right) - C\left( x \right)}}{x}\).

b) Tìm lợi nhuận trung bình khi mức sản xuất \(x\) lần lượt là \(100,{\rm{ }}500\) và \(1{\rm{ }}000\) đơn vị sản phẩm.

c) Xét tính đơn điệu của hàm lợi nhuận trung bình \(\bar P\left( x \right)\) trên khoảng \(\left( {0; + \infty } \right)\) và tính giới hạn của hàm số này khi \(x \to + \infty \). Giải thích ý nghĩa thực tiễn của kết quả nhận được.

Xem lời giải >>

Bài 7 :

Một con lắc lò xo, gồm một vật nặng có khối lượng \(1\) kg được gắn vào một lò xo được cố định một đầu, dao động điều hòa với biên độ \(A = 0,24\) m và chu kì \(T = 4\) giây. Vị trí \(x\) (mét) của vật tại thời điểm \(t\) được cho bởi \(x\left( t \right) = A\cos \left( {\omega t} \right)\), trong đó \(\omega = \frac{{2\pi }}{T}\) là tần số góc và thời gian \(t\) tính bằng giây.

a) Tìm vị trí của vật tại thời điểm \(t\) và tại thời điểm \(t = 0,5\) giây.

b) Tìm vận tốc \(v\) của vật tại thời điểm \(t\) giây và tìm vận tốc của vật khi \(t = 0,5\) giây.

c) Tìm gia tốc \(a\) của vật.

d) Sử dụng định luật thứ hai của Newton \(F = ma\), tìm độ lớn và hướng của lực tác dụng lên vật khi \(t = 0,5\) giây.

e) Tìm thời gian tối thiểu để vật chuyển động từ vị trí ban đầu đến vị trí \(x = - 0,12\) m. Tìm vận tốc của vật khi \(x = - 0,12\) m.

Xem lời giải >>

Bài 8 :

Một vật chuyển động dọc theo một trục số nằm ngang, chiều dương từ trái sang phải. Giả sử vị trí của vật \(x\) (mét) từ thời điểm \(t = 0\) giây đến thời điểm \(t = 5\) giây được cho bởi công thức \(x\left( t \right)={{t}^{3}}-7{{t}^{2}}+11t+5\).

a) Xác định vận tốc \(v\) của vật. Xác định khoảng thời gian vật chuyển động sang phải và khoảng thời gian vật chuyển động sang trái.

b) Tìm tốc độ của vật và thời điểm vật dừng lại. Tính tốc độ cực đại của vật trong khoảng thời gian từ \(t = 1\) đến \(t = 4\) giây.

c) Xác định gia tốc \(a\) của vật. Tìm khoảng thời gian vật tăng tốc và khoảng thời gian vật giảm tốc.

Xem lời giải >>

Bài 9 :

Lợi nhuận thu được \(P\) của một công ty khi dùng số tiền \(s\) chi cho quảng cáo được cho bởi công thức

\(P = P\left( s \right) = - \frac{1}{{10}}{s^3} + 6{s^2} + 400,{\rm{ s}} \ge 0\).

Ở đây các số tiền được được tính bằng đơn vị nghìn USD.

a) Tìm số tiền công ty phải chi cho quảng cáo để mang lại lợi nhuận tối đa.

b) Lợi nhuận thu được của công ty thay đổi thế nào khi số tiền chi cho quảng cáo thay đổi?

Xem lời giải >>

Bài 10 :

Một chiếc xe nhỏ chuyển động không có ma sát, gắn vào tường bằng một lò xo (xem hình vẽ), được kéo ra khỏi vị trí đứng yên \(10\) cm rồi thả ra tại thời điểm ban đầu \(t = 0\) giây để chuyển động trong \(4\) giây. Vị trí \(s\) (cm) tại thời điểm \(t\) giây là \(s = 10\cos \pi t\).

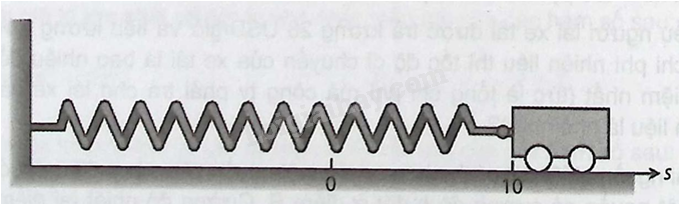
a) Tốc độ lớn nhất của xe là bao nhiêu? Khi nào xe chuyển động với tốc độ như vậy, khi đó xe đang ở vị trí nào và gia tốc lúc đó có độ lớn là bao nhiêu?

b) Xe ở đâu khi độ lớn gia tốc là lớn nhất? Khi đó vận tốc của xe là bao nhiêu?

Xem lời giải >>

Bài 11 :

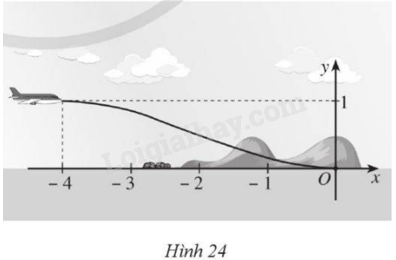
Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó khi gắn với hệ trục toạ độ \(Oxy\) được mô phỏng ở Hình 24. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có toạ độ \(\left( { - 4;1} \right)\) là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc toạ độ là điểm cực tiểu của đồ thị hàm số.

a) Tìm công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn \(\left[ { - 4;0} \right]\).

b) Khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất bao nhiêu dặm? (Biết đơn vị trên hệ trục toạ độ là dặm).

c) Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang bao nhiều dặm?

Xem lời giải >>

Bài 12 :

Một chất điểm chuyển động lên, xuống theo phương thẳng đứng. Độ cao \(h\left( t \right)\) của chất điểm tại thời điểm \(t\) (giây) được cho bởi công thức

\(h\left( t \right) = \frac{1}{3}{t^3} - 4{t^2} + 12t + 1\) với \(0 \le t \le 8\).

a) Viết công thức tính vận tốc của chất điểm.

b) Trong khoảng thời gian nào chất điểm chuyển động lên, trong thời gian nào chất điểm chuyển động đi xuống?

Xem lời giải >>

Bài 13 :

Người ta thấy rằng trong vòng 3 năm tính từ đầu năm 2020, giá thành \(P\) của một loại sản phẩm vào tháng thứ \(t\) thay đổi theo công thức \(P\left( t \right) = 80{t^3} - 3600{t^2} + 48000t + 100000\) (đồng) với \(0 \le t \le 36\).

Hãy cho biết trong khoảng thời gian nào giá thành sản phẩm tăng, trong khoảng thời gian nào giá thành sản phẩm giảm. Giá thành đạt cực đại và cực tiểu vào thời điểm nào?

Xem lời giải >>

Bài 14 :

Chọn đúng hoặc sai cho mỗi ý a, b, c, d.
Lợi nhuận một xưởng thu được từ việc sản xuất một mặt hàng được cho bởi công thức \(P\left( q \right) = - {q^3} + 24{q^2} + 780q - 5000\) (nghìn đồng) trong đó \(q\) (kg) là khối lượng sản phẩm sản xuất được. Xưởng chỉ sản xuất được tối đa 50 kg sản phẩm trong một tuần.
a) Xưởng sản xuất càng nhiều thì lợi nhuận càng cao.
b) Lợi nhuận lớn nhất khi xưởng sản xuất 26 kg sản phẩm trong một tuần.
c) Sau khi sản xuất được 26 kg sản phẩm, càng sản xuất thêm thì lợi nhuận càng giảm.
d) Lợi nhuận của xưởng thấp nhất khi không sản xuất.

Xem lời giải >>

Bài 15 :

Doanh thu \(R\) (USD) từ vệc cho thuê \(x\) căn hộ có thể được mô hình hóa bằng hàm số

\(R = 2x\left( {900 + 32x - {x^2}} \right)\).

a) Tìm hàm doanh thu biên.

b) Tìm doanh thu biên khi \(x = 14\) và giải thích ý nghĩa thực tiễn của nó.

c) Tìm lượng doanh thu tăng thêm khi số căn hộ cho thuê tăng từ \(14\) lên \(15\).

Xem lời giải >>

Bài 16 :

Cho hàm số \(y = {x^3} + 3{x^2} + 1\) có đồ thị (C). Xét đường thẳng đi qua điểm \(A\left( { - 3;1} \right)\) và có hệ số góc k. Điều kiện của k để đường thẳng đó cắt đồ thị (C) tại ba điểm phân biệt.

A. \(0 < k < 1\).

B. \(k > 0\).

C. \(1 < k < 9\).

D. \(0 < k \ne 9\).

Xem lời giải >>

Bài 17 :

Tất cả các giá trị thực của tham số m để đường thẳng \(y = x + m - 1\) cắt đồ thị hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) tại hai điểm A, B thỏa mãn \(AB = 2\sqrt 3 \) là

A. \(m = 2 \pm \sqrt {10} \).

B. \(m = 4 \pm \sqrt 3 \).

C. \(m = 2 \pm \sqrt 3 \).

D. \(m = 4 \pm \sqrt {10} \).

Xem lời giải >>

Bài 18 :

Một công ty sản xuất một sản phẩm. Bộ phận tài chính của công ty đưa ra hàm giá bán là p(x) = 1000 - 25x, trong đó p(x) (triệu đồng) là giá bán của mỗi sản phẩm mà tại giá bán này có x sản phẩm được bán ra. Doanh thu của công ty khi bán được 5 sản phẩm là bao nhiêu triệu đồng?

Xem lời giải >>

Bài 19 :

Một vật chuyển động thẳng được cho bởi phương trình: \(s(t) = - \frac{1}{3}{t^3} + 4{t^2} + 9t\), trong đó t tính bằng giây và s tính bằng mét.

a) Vận tốc của vật tại các thời điểm t = 3 giây là v(3) = 1 m/s.

b) Quãng đường vật đi được từ lúc bắt đầu chuyển động đến khi vật dừng yên là 162(m).

c) Gia tốc của vật tại thời điểm t = 3 giây: a(3) = 2 \(m/{s^2}\).

d) Trong 9 giây đầu tiên, vật tăng tốc khi \(t \in \left[ {0;4} \right]\).

Xem lời giải >>

Bài 20 :

Một vât được phóng thẳng đứng lên trên từ mặt đất với tốc độ ban đầu là 32,5 m/s (bỏ qua sức cản của không khí), độ cao (tính bằng mét) của vật sau t giây được cho bởi công thức \(h(t) = 32,5t - 4,9{t^2}\). Vận tốc của vật sau 3 giây bằng bao nhiêu m/s?

Xem lời giải >>

Bài 21 :

Cho hàm số \(f(x) = 2{x^3} - 3(m + 1){x^2} + 6mx + 1\), với \(m\) là tham số thực.

Xem lời giải >>

Bài 22 :

Sự phân hủy của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hòa tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (\(t \ge 0\)) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số \(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\).

a) Vào thời điểm t = 1 thì nồng độ oxygen trong nước là 3,5 (mg/l).

b) Nồng độ oxygen (mg/l) trong hồ nước không vượt quá 5 (mg/l).

c) Vào thời điểm t = 0 thì nồng độ oxygen trong nước cao nhất.

d) Nồng độ oxygen (mg/l) trong hồ nước thấp nhất là 3,5 (mg/l).

Xem lời giải >>

Bài 23 :

Một hạt chuyển động trên một đường thẳng có gắn một trục tọa độ với gốc tọa độ là vị trí hạt bắt đầu chuyển động. Tọa độ của hạt trên trục tại thời điểm t (đơn vị: giây) kể từ khi xuất phát được cho bởi công thức x(t) = 2t – 3ln(t + 1) (đơn vị: mét), \(t \ge 0\). Hàm số v(t) = x’(t) (đơn vị: mét/giây) biểu thị vận tốc chuyển động của hạt.

a) Quãng đường mà hạt đi được trong 3 giây đầu tiên là 1,84 m (làm tròn kết quả đến hàng phần trăm).

b) Hạt đứng yên tại thời điểm t = 0,5 s.

c) \(v(t) = 2 - \frac{3}{{t + 1}}\).

d) Vận tốc ban đầu của hạt là 1 m/s.

Xem lời giải >>

Bài 24 :

Cho hàm số f(x) = 92 – 20ln(x + 1).

a) Bất phương trình \(f(x) \ge 72\) có đúng 3 nghiệm nguyên.

b) Một nghiên cứu chỉ ra rằng sau khi tham gia một khóa học, phần trăm kiến thức sinh viên còn nhớ sau t tháng kết thúc khóa học được xác định bởi hàm số y =f(t), trong đó f(t) được tính bằng % và \(0 \le t \le 24\). Phầm trăm kiến thức sinh viên còn nhớ là 50% khi t = 7 (kết quả làm tròn đến hàng đơn vị).

c) Tập xác định của hàm số y = f(x) là \(D = ( - 1; + \infty )\).

d) Hàm số f(x) nghịch biến trên khoảng \(( - 1; + \infty )\).

Xem lời giải >>

Bài 25 :

Một bể chứa 6000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ 25 gam muối cho mỗi lít nước với tốc độ 20 lít/phút. Giả sử sau t phút, tỉ số giữa khối lượng muối trong bể và thể tích nước trong bể (đơn vị: gam/lít) là một hàm f(t). Xác định hàm số f(t), \(t \in [0; + \infty )\). Nồng độ muối tối đa có trong bể bằng bao nhiêu?

Xem lời giải >>

Bài 26 :

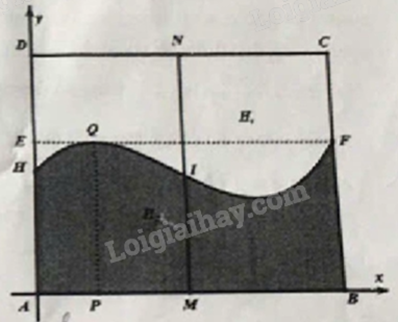
Khuôn viên của một công viên có dạng hình chữ nhật ABCD với AB = 100 m; AD = 80 m. Người ta muốn chia công viên thành hai khu gồm một khu dành cho trẻ em, một khu dành cho người lớn. Để tạo thiết kế độc đáo và lạ mắt người ta dùng một đường cong chia khuôn viên thành hai phần H, (không tô màu) dành cho người lớn và H, (tô màu) dành cho trẻ em như hình vẽ bên với AH = 40 m; AE = 50 m; AP = 20 m và EF // AB; PQ // AD.

Biết rằng khi xét trong một hệ toạ độ Oxy, đường cong trong hình là một phần của một đồ thị hàm số bậc ba. Phần chính giữa của công viên người ta muốn mắc dây đèn trang trí dọc theo đoạn thẳng MN như hình. Biết giá tiền mỗi mét dây trang trí của phần dành cho trẻ em là 120 nghìn đồng và phần dành cho người lớn là 200 nghìn đồng. Tổng số tiền mắc dây đèn trang trí trên đoạn MN là bao nhiêu triệu đồng?

Xem lời giải >>

Bài 27 :

Cho hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\)có đồ thị như hình vẽ.

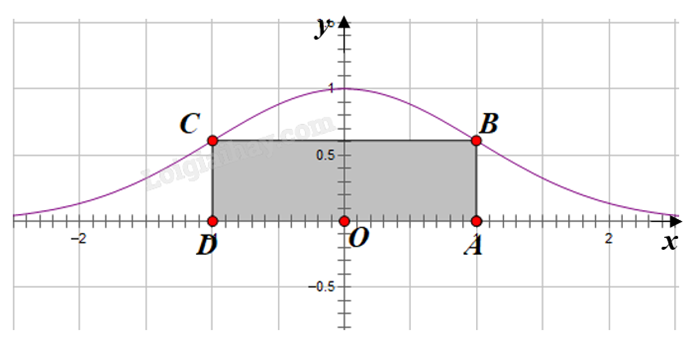
Biết ABCD là hình chữ nhật thay đổi sao cho hai điểm B, C luôn thuộc đồ thị hàm số đã cho. Hai điểm A, D nằm trên trục hoành (điểm A thuộc tia Ox).

a) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có tập xác định \(D = \mathbb{R}\).

b) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có đạo hàm là \(y' = f'\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).

c) Khi điểm B có toạ độ \(\left( {x;{e^{ - \frac{1}{2}{x^2}}}} \right)\) với \(x > 0\) thì diện tích ABCD là \(S\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).

d) Diện tích hình chữ nhật ABCD đạt giá trị lớn nhất khi AD = 2.

Xem lời giải >>

Bài 28 :

Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức \(s(t) = {t^3} - 9{t^2} + 15t\), \(t \ge 0\). Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?

Xem lời giải >>

Bài 29 :

Trong 20 phút theo dõi, lưu lượng nước của một con sông được tính theo công thức

\(Q(t) = - \frac{1}{5}{t^3} + 5{t^2} + 100\),

trong đó Q được tính theo \({m^3}\)/phút, t tính theo phút, \(0 \le t \le 20\) (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016). Khi lưu lượng nước của con sông lên đến 550 \({m^3}\)/phút thì cảnh báo lũ được đưa ra. Trong thời gian theo dõi, lưu lượng nước của con sông lớn nhất là bao nhiêu? Cảnh báo lũ được đưa ra vào thời điểm nào?

Xem lời giải >>

Bài 30 :

Một hồ nước ở Bắc Ontario đã phục hồi sau một vụ tràn axit khiến tất cả cá hồi ở đó chết. Một chương trình tái thả cá đã thả 800 con cá hồi vào hồ. Ba năm sau, số lượng được ước tính là 6000 con. Sức chứa của hồ nước được cho là 8000 con. Để đánh giá khả năng tăng trưởng, người ta mô phỏng số lượng cá trong hồ qua từng năm thông qua hàm số \(P(t) = \frac{c}{{1 + a.{b^{ - t}}}}\) \(\left( {a,b,c \in \mathbb{R}} \right)\) như hình vẽ bên dưới (trong đó t tính theo năm kể từ lúc bắt đầu thả cá vào hồ).

Sử dụng mô hình trên, hãy tính tốc độ tăng trưởng tối đa (đơn vị: con/năm) của đàn cá. Kết quả làm tròn đến hàng đơn vị).

Xem lời giải >>